『力扣和笔试算法』科大讯飞研发岗笔试(2020-08-29)！

科大讯飞研发岗笔试(2020-08-29)！

一. 第1题

1.1. 题目描述

• 题目描述： 一个m*n的矩阵，矩阵的数值代表礼物的价值，从矩阵的左上角出发，并且每次 向右或者向下(不能回退) 移动一格，直到到达矩阵的右下角。计算所走的路径礼物价值加起来最大是多少？
• 样例输入：

3, 3 //m, n表示矩阵的长宽，要求m或者n不超过100；
2, 3, 1
1, 5, 1
4, 2, 1

• 样例输出：

13

1.2. 算法实现

• 动态规划问题，解题思路： 将大问题，分解为小问题，解题关键每次只能向下或者向右移动一步。可以知道, 任意点的路径总和等于元素上面的值或元素左边的值再加上本身，就是路径总和，在两个路径和中取最小的路径，得到的就是最小路径。
• 第一步: 创建一个大小一样的二维数组, 并将新数组的左上角与求解数据的值取为一样

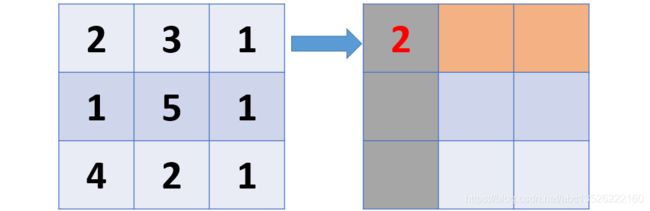
• 第二步: 计算出新数组中，第一行，第一列的值(因为第一行没有上一行，第一列没有上一列，所以他们的值是确定的，可以计算得出)。依次类推, 算出第一行数据以及第一列数据。(下面我们程序中并没有新建矩阵，这里为了直观理解)

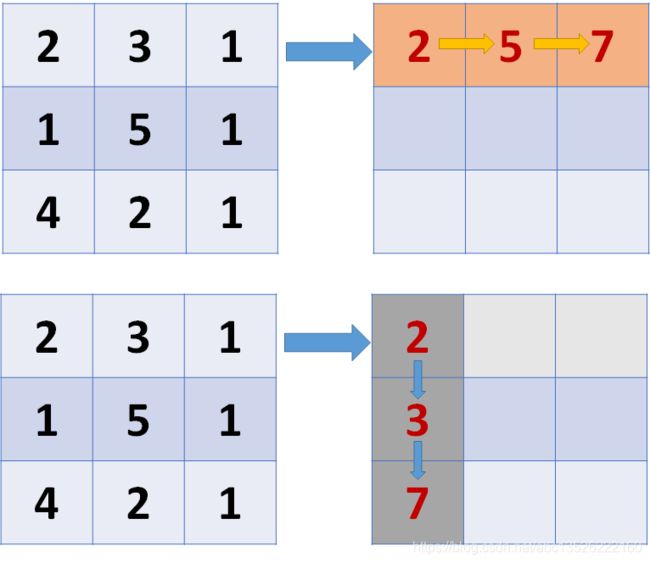
• 至此, 我们已经求解出，第一行和第一列的值，然后我们要求解中间的值，中间的值会存在两种情况，可能和上方的值相加，可能和左边的值相加，需取其大的值。

• 下面是程序实现，直接AC。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class Solution
{
     
public:
    void maxValue(vector<vector<int>> &arr, int m, int n)
    {
     
        int value = 0;
        if (m <= 0 || n <= 0)
            cout << value << endl;
        else
        {
     
            for (int i = 1; i < m; i++) //第1列
                arr[i][0] += arr[i - 1][0];
            for (int j = 1; j < n; j++) //第1行
                arr[0][j] += arr[0][j - 1];
            for (int i = 1; i < m; i++) //中间的值
                for (int j = 1; j < n; j++)
                    arr[i][j] += max(arr[i - 1][j], arr[i][j - 1]); //左边或者上边最大的值。
            cout << arr[m - 1][n - 1] << endl;
        }
    }
};
int main()
{
     
    Solution sol;
    int m, n;
    cin >> m;
    if (cin.get() == ',')  //cin.get()用来接收字符
        cin >> n;
    vector<vector<int>> arr(m, vector<int>(n, 0));
    for (int i = 0; i < m; i++)
        for (int j = 0; j < n; j++)
            cin >> arr[i][j];
    sol.maxValue(arr, m, n);
    system("pause");
    return 0;
}

4,5
1 2 3 4 6
3 2 5 7 1
2 4 5 7 9
9 8 3 2 1
35
请按任意键继续. . .

1.3. 补充C++输入

#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main()
{
     
    //==================================1、整行读取
    string s;
    getline(cin, s); //整行读取
    cout << s << endl;
    system("pause");
    return 0;
}

abded efeg  egd
abded efeg  egd
请按任意键继续. . .

#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main()
{
     
    vector<int> arr;
    int tmp;
    while (cin >> tmp)
    {
     
        arr.push_back(tmp);
        if (cin.get() == '\n')
            break;
    }
    for (int i = 0; i < arr.size(); i++)
        cout << arr[i]<<" ";
    system("pause");
    return 0;
}

1,2,3,4,5,6,6,7,7,8,9
1 2 3 4 5 6 6 7 7 8 9 请按任意键继续. . .

二. 第2题

2.1. 题目描述

• 题目描述： 某种排序方法对关键字序列 $\{25,84,21,47,15,27,68,35,20\}$，排序过程中序列变化如下：
• $\{15,84,21,47,25,27,68,35,20\}$
• $\{15,20,21,25,27,35,68,47,84\}$
• $\{15,20,21,25,27,35,47,68,84\}$

• 样例输入：

9 									// 关键字的个数
25, 84, 21, 47, 15, 27, 68, 35, 20  // 具体关键字的值

• 样例输出：

15,20,21,25,27,35,47,68,84

2.2. 算法实现

• C++ STL vector添加元素( push_back()和emplace_back() )详解

三. 第3题

3.1. 题目描述

• 题目描述： 字符串前后所有以及中间多于一个的下划线被称为“多余下划线”，设计程序实现在原串上进行去除多余下划线操作(注意： 新定义并开辟与原来数组大小相同数组进行去除不得分)。

• 样例输入：

___abc__bde___bded____

• 样例输出：

abc_bde_bded

3.2. 算法实现

• 下面是程序实现，AC80%。

#include <iostream>
#include <string>
using namespace std;

class Solution
{
     
public:
    /*存在不好的地方，string并不是以\0结尾*/
    void delStr(string &s)
    {
     
        int m = 0, n = 0;
        while (s[m] == '_') //找出字符串前面不是_的下标
            m++;
        while (s[m] != '\0')
        {
     
            if (s[m] == '_' && s[m + 1] == '_' || s[m + 1] == '\0') //中间_
            {
     
                m++;
                continue; //进行下一个循环，也就是遍历下一个字符
            }
            s[n++] = s[m++];
        }
        for (int i = 0; i < n; i++)
        {
     
            cout << s[i];
        }
        cout << endl;
    }
};
int main()
{
     
    Solution sol;
    string s;
    cin >> s;
    if (!s.empty())
        sol.delStr(s);
    system("pause");
    return 0;
}

四. 第4题

4.1. 题目描述

• 题目描述： 设计一个递归实现将一个正整数分解质因数，如50=255，程序打印“255”，每个素因子之间使用*隔开。如果这个数本身是素数，则直接输出该数。

• 样例输入：

50

• 样例输出：

2*5*5

4.2. 算法实现

• 下面是程序实现，直接AC。

#include <iostream>
using namespace std;

class Solution
{
     
public:
    void toZhiyinshu(int n)
    {
     
        int i, j;
        for (i = 2; i <= n; i++) //判断是不是质数；
        {
     
            if (n % i == 0) //是质数；
            {
     
                j = n / i;
                if (j == 1)
                {
     
                    cout << i;
                    return;
                }
                else
                {
     
                    cout << i << "*";
                    toZhiyinshu(j);
                    break;
                }
            }
        }
        cout << endl;
    }
};
int main()
{
     
    Solution sol;
    int n;
    cin >> n;
    sol.toZhiyinshu(n);
    system("pause");
    return 0;
}

五. 参考文章

• 参考：LeetCode-64. 最小路径和