【实时碰撞检测算法Summary】k-DOP碰撞检测
K-DOP名词解释
平行平面包围体,不过平行平面是轴对齐的。利用一个法线和两个浮点数值来确定平行平面的位置。而这个法线分量一般限制在(+-1,+-1,+-1)中。
k越多,包围盒的拟合效果就越好,而且由于物体之间的法线可以共享(都是限制的),所以存储空间也会减小,k-DOP只需要存储每个轴的最大最小值就可以了。
如DOP8存储如下
6-DOP一般称作多面体,如果各个面都与坐标轴平行,那就是AABB。
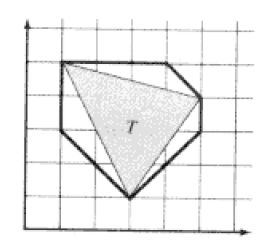
下图是一个2D空间中8-DOP的例子
K-DOP最大的缺陷:即使空间中的物体很少碰撞,也需要对包围盒执行更新/翻转操作,来重新确定该轴上的最大/最小值
所以一般情况下,先用球体或者其他的什么简单的 包围盒做一次一级测试,如果通过了再做K-DOP
K-DOP的计算方法如下:
提升K-DOP检测效率的方法:
一般情况下我们认为,两个平面如果法线相近,那么相交结果也是相近的。所以我们在做K-DOP测试的时候,一般下一个测试的平面尽可能的和上一个测试平面正交。