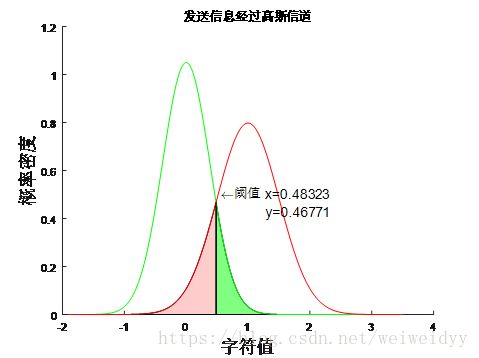
求高斯信道的信道容量 信息论

clear,clc;

%一维二元高斯信道的信道容量

xn=8000;%定义点数

m1=0;

m2=1;%信号参数

sigma1=0.38;

sigma2=0.5;%高斯噪声参数

xmin=min([m1-5*sigma1,m2-5*sigma2]);xmax=max([m1+5*sigma1,m2+5*sigma2]);%定义域边界

x=linspace(xmin,xmax,xn+1);

y1=(((2*pi)^(-0.5))/sigma1)*exp(-(x-m1).^2/(2*(sigma1^2)));

y2=(((2*pi)^(-0.5))/sigma2)*exp(-(x-m2).^2/(2*(sigma2^2)));%信号受干扰后的概率密度分布函数

a=(sigma2^2-sigma1^2)/(2*sigma1^2*sigma2^2);

b=(2*m2*sigma1^2-2*m1*sigma2^2)/(2*sigma1^2*sigma2^2);

c=(sigma2^2*m1^2-sigma1^2*m2^2)/(2*sigma1^2*sigma2^2)-log(sigma2/sigma1);%联立y1,y2解二次方程求阈值

if a==0

    x4=c/b;%二次项系数为0

else

    x4=(-b+sqrt(b^2-4*a*c))/(2*a);%二次项系数不为0

end

y4=(((2*pi)^(-0.5))/sigma1)*exp(-(x4-m1).^2/(2*(sigma1^2)));

y5=[0 y1((xn+1-round(((xmax-x4)/(xmax-xmin))*xn)+1):1:xn+1)];

t1=x(xn+1-round(((xmax-x4)/(xmax-xmin))*xn):xn+1);

patch(t1,y5,[0.5 1 0.5]);%错误概率区域1绘制

hold on;

y6=[y2(1:round((abs(xmin-x4))*xn/(xmax-xmin))-1) 0];

t2=x(1:round((abs(xmin-x4))*xn/(xmax-xmin)));

patch(t2,y6,[1 0.8 0.8]);%错误概率区域2绘制

plot(x,y1,'-g',x,y2,'-r',[x4 x4],[0 y4],'black');%概率密度曲线绘制

xlabel('字符值','Rotation',0,'fontsize',16);

ylabel('概率密度','Rotation',90,'fontsize',16);

title('发送信息经过高斯信道');

text(x4,y4,{[' \leftarrow阈值 x=',num2str(x4)];['             y=',num2str(y4)]},'fontsize',12);%阈值绘制

dx=0.001;

l=abs(x4-xmin);

nd=round(l/dx);ff1=[];ff2=[];

for i=1:nd

    f1=(((2*pi)^(-0.5))/sigma1)*exp(-((i*dx-abs(xmin))-m1).^2/(2*(sigma1^2)));

    f2=(((2*pi)^(-0.5))/sigma2)*exp(-((i*dx-abs(xmin))-m2).^2/((2*sigma2^2)));

    ff1(i)=f1*dx;

    ff2(i)=f2*dx;

end

I1=sum(ff1);

I2=1-I1;

I3=sum(ff2);

I4=1-I3;

Py_x=[I1 I2;I3 I4];%通过积分解得信道概率转移矩阵

[m,n]=size(Py_x);

Ix=[];Cxy=[];b2=[];

for t=1:999

    b2(1)=t*0.001;

    b2(2)=1-b2(1);%先验概率

    Px=b2';

    [m2,n2]=size(Px);

for i=1:m

    Ix(i,1)=Px(i,1)*(-log2(Px(i,1)));%自信息量

end

Hx=sum(Ix);%先验信息熵

Iy_x=[];Pxy=[];

for j=1:m

    for i=1:n

        Pxy(j,i)=Px(j,1)*Py_x(j,i);%条件概率

        Iy_x(j,i)=Pxy(j,i)*(-log2(Py_x(j,i)));

        I3(j,i)=Pxy(j,i)*(-log2(Pxy(j,i)));

    end

end

Hy1x=sum(sum(Iy_x));

Hxy=sum(sum(I3));%联合熵

Py=sum(Pxy);Iy=[];

for i=1:n

    Iy(i)=Py(i)*(-log2(Py(i)));

end

Hy=sum(Iy);

Hx1y=Hxy-Hy;

Ixy=Hy-Hy1x;%互信息

Cxy(t)=Ixy;

end

[Cn Cm]=max(Cxy);%找到互信息的最大值即信道容量

C=Cn;

fprintf("信道容量为:"+C)