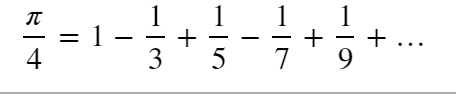数据结构与算法学习笔记(python)——第一节 数组应用程序实战

前言

本人是一个长期的数据分析爱好者，最近半年的时间的在网上学习了很多关于python、数据分析、数据挖掘以及项目管理相关的课程和知识，但是在学习的过程中，过于追求课程数量的增长，长时间关注于学习了多少多少门课程。事实上，学完一门课之后真正掌握的知识并不多，主要的原因是自己没有认真学习和理解温故而知新的这句话的真正含义。因此，从现在开始，我在学习《数据结构与算法——基于python》的课程内容之后，抽出固定的时间对每天学习的内容进行总结和分享，一方面有助于个人更好的掌握课程的内容，另一方面能和大家一起分享个人的学习历程和相应的学习知识。

第一节 数组应用程序实战

在老师对课程做了简单介绍之后，就给大家抛出了几个简单的数据结构问题；现将每个问题、解题思路和详细代码记录如下；

1. Arry应用1——计算一元二次方程的解 ；
   思路：
   对于一元二次方程组，有如下的求解方法；
   aX^2+bX+c=0
   如果 b-4ac >= 0，则 x1,x2= [-b±√(b^2-4ac)]/2a
   如果 b-4ac < 0，则 无解
   代码

def solve(a, b, c):
    r = pow(b, 2) - 4 * a * c
    if (r < 0):
        raise ValueError("No Solution") 
    return (-b + math.sqrt(r)) / (2 * a), (-b - math.sqrt(r)) / (2 * a)
solve(1, 4, 1) # 1，4,1 分别表示方程中的a，b，c

2. Arry应用2——比赛现场计分系统
   问题描述：
   一个歌唱比赛的歌手打分，设计一个程序帮助现场去掉一个最低分和一个最高分，再计算一 个平均分；
   思路：
   根据选手的分数得到最高分和最低分，然后去掉一个最高分和一个最低分，计算平均分即可
   代码

def singing_score(values):
    small_pos = 0
    for i in range(1, len(values)): # 找出最低分
        if values[i] < values[small_pos] :
            small_pos = i 
            
    high_pos = 0
    for i in range(1, len(values)): # 找出最高分
        if values[i] > values[high_pos] :
            high_pos = i
    values.remove(values[small_pos]) #  去掉一个最高分
    values.remove(values[high_pos]) # 去掉一个最低分
    rst = sum(values)/len(values) # 求平均分
    return rst
values =  [8,9,5,10,5,8,7,9,9.5]
singing_score(values)

3. Arry应用3——计算圆周率的值；
   方法1：
   
   代码

def pi1(n):
    pi = 0
    sign = 1
    for i in range(1, n + 1, 2):
        pi += sign * (1 / i)
        sign *= -1
    return pi * 4
 pi1(10000)

*或者 *

def pi2():
    pi = 0
    sign = 1
    pre = 999
    i = 1
    delta = 0.000001
    
    while (abs(pi - pre) > delta):
        pre = pi
        pi += sign * (1 / i)
        sign *= -1
        i += 2
    return pi * 4  
pi2()

方法2 蒙特卡洛模拟
思路：
想象一个圆形靶子，我们不停的向靶面射击, 命名圆内的我们算是“击中 也就是 2+2≤1 .
假如我们不停的射击，直到我们把这个方形的靶子全部覆盖(打成了骰子)
圆的面积应该是 =2
方形的面积应该是
=^2
也就是说
/=^2/ ^2
=1,=2
hits / tries is approximately equal to the ratio of the areas of the circle 那么/=/4
那么预估的 =4×(/)
代码

from random import random

def pi3(TRIES):
    hits = 0
    for i in range(TRIES) :
        # Generate two random numbers between –1 and 1
        r = random()
        x = -1 + 2 * r
        r = random()
        y = -1 + 2 * r
        # Check whether the point lies in the unit circle
        if x * x + y * y <= 1 :
            hits = hits + 1

        # The ratio hits / tries is approximately the same as the ratio
        # circle area / square area = pi / 4.
    return 4.0 * hits / TRIES
pi3(100)

4. Arry应用4——打印9X9乘法口诀表
   代码

for i in range(1,10):
	for j in range(1,i+1):
		print(j, "*", i,"=",i*j,end = " ")
	print 

5. Arry应用5——设计一个洗牌程序
   问题描述：
   假设现在有1到10按照顺序排列，需要设计一个程序将这个数列变成乱序的数列，使得每个元素出现在每个位置的概率相同；
   思路：
   利用随机数将数据元素更换顺序
   方法1： 用random.shuffle()函数
   代码
   构造随机替换函数

import random
def shuffle_system(cards):
    random.shuffle(cards)  

检验每个元素在每个位置出现的概率

def test_shuffle(f):
    result = [[0 for i in range(10)] for j in range(10)]

    for i in range(1000):
        A = [i for i in range(0, 10)]
        f(A)
        for j in range(len(A)):
            result[A[j]][j] += 1
        
    print('\n'.join([''.join(['{:6}'.format(item) for item in row]) 
          for row in result]))
test_shuffle(shuffle_system)

输出结果：

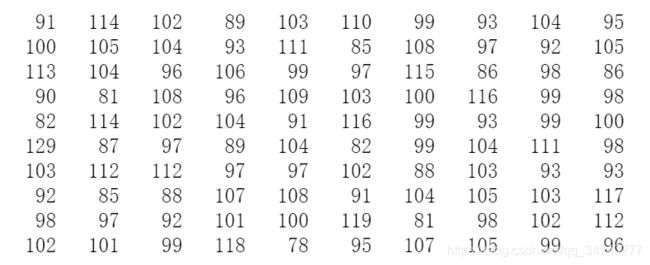
从输出结果可以看出，将上述随机替换函数执行1000次，得到每个数出现在每个位置的次数基本为100，说明上述函数较为合理；
方法2： 随机生成两个数，并交换位置
代码

def shuffle_1st(cards):
    for k in range(len(cards)):
        i = random.randint(0, len(cards) - 1)
        j = random.randint(0, len(cards) - 1)
        cards[i], cards[j] = cards[j], cards[i]

利用test_shuffle（）检验每个元素在每个位置出现的概率

test_shuffle(shuffle_1st)

输出结果：

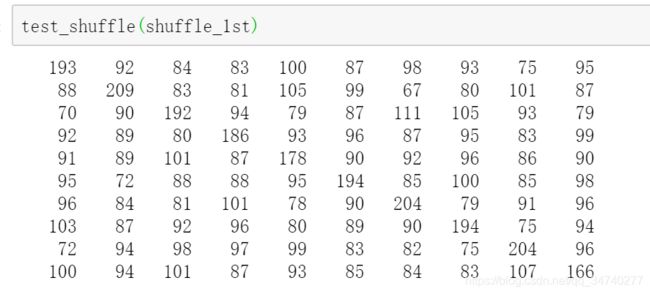
从输出结果可以看出，将上述随机替换函数执行1000次，得到每个数出现在每个位置的次数不相等，对角线上的输出结果较大，说明上述洗牌函数随机性不强，使结果不能均匀分布。
方法3： 随机生成一个数，i与这个数相加，然后交换元素的位置
代码

def shuffle_correct(cards):
    for i in range(len(cards)):
        randomi = i + random.randint(0, (len(cards) - i - 1))
        cards[i], cards[randomi] = cards[randomi], cards[i]

利用test_shuffle（）检验每个元素在每个位置出现的概率

test_shuffle(shuffle_correct)	

输出结果

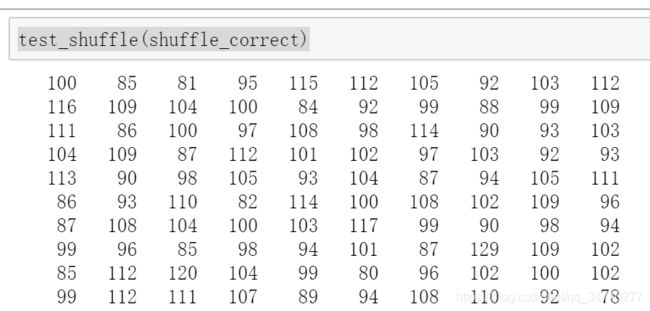
从输出结果可以看出，将上述随机替换函数执行1000次，得到每个数出现在每个位置的次数不相等，但是总体差别不大，说明上述洗牌函数随机性较强，使结果能均匀分布。
6. Arry应用6——计算素数 (质数)
问题描述：
给定一个正整数n，计算出小于等于n的质数有多少个。 比如17，则返回7，因为小于等于7的质数有2，3，5，7，13，17；
思路：
对从2到根号n的数，排除每个数的倍数，剩下的即为质数，然后剩下的质数输出并计数即可。
代码

def count_prime(n):
    is_prime = [True] * (n + 1)
    i = 2
    while (i * i <= n):
        if (is_prime[i]):
            j = i
            while (j * i <= n): # i从2到100，将i的倍数全部变为false
                is_prime[i * j] = False
                j += 1
        i += 1    
    # is_prime[i] 为True的序号全为质数，输出即可
    count = 0
    for i in range(2, n+1):
        if (is_prime[i]):
            count += 1
            print(i, end = " ") # 输出每个质数
    return count # 输出质数的个数

计算100以内的质数计个数

count_prime(1000)

输出即可得到每个质数及个数，如下图所示；

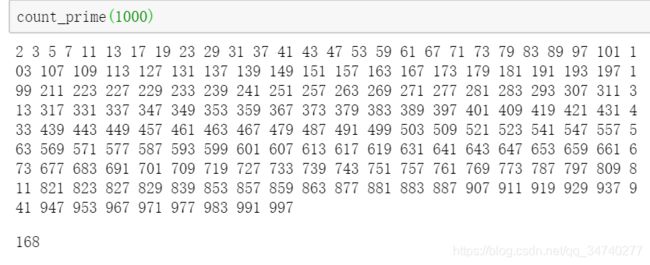
7. Arry应用7——证明哥德巴赫猜想
问题描述：
1742年，哥德巴赫提出了著名的哥德巴赫猜想。即：任一大于2的偶数都可写成两个质数之和。比如说16=3+13。试着编码写出程序：只包含N作为参数并且给出N为两个质数之和的表达式。哥德巴赫猜想至今没有被证明，但是目前已知其在N小于10^14的时候都是成立的；
思路：
根据计算质数的思路得到n以内的所有质数，然后对于满足相加等于n的质数进行筛选并输出即可，在寻找满足相加等于n的质数时，可先将质数从小到大排序，再从首尾两端相加，即可快速确定。
代码

def goldbach(n):
    is_prime = [True] * (n + 1)
    i = 2
    while (i * i <= n):
        if (is_prime[i]):
            j = i
            while (j * i <= n):
                is_prime[i * j] = False
                j += 1
        i += 1
    count = 0
    for i in range(2, n+1):
        if (is_prime[i]):
            count += 1

    primes = [None] * count 
    
    idx = 0
    for i in range(2, n + 1):
        if (is_prime[i]): # 将质数赋值给primes数组
            primes[idx] = i
            idx += 1
    left = 0
    right = count - 1
    while (left < right):
        if (n == primes[left] + primes[right]):
            print(n," = ", primes[left], " + ", primes[right])
            left += 1
            right -= 1
        elif (n > primes[left] + primes[right]):
            left += 1
        else:
            right -= 1
goldbach(100)

输出结果为100拆解成两个质数之和，如下所示；

持续更新，欢迎大家点赞收藏