数据结构与算法学习笔记(python)——第5节 二分搜索
前言
本人是一个长期的数据分析爱好者,最近半年的时间的在网上学习了很多关于python、数据分析、数据挖掘以及项目管理相关的课程和知识,但是在学习的过程中,过于追求课程数量的增长,长时间关注于学习了多少多少门课程。事实上,学完一门课之后真正掌握的知识并不多,主要的原因是自己没有认真学习和理解温故而知新的这句话的真正含义。因此,从现在开始,我在学习《数据结构与算法——基于python》的课程内容之后,抽出固定的时间对每天学习的内容进行总结和分享,一方面有助于个人更好的掌握课程的内容,另一方面能和大家一起分享个人的学习历程和相应的学习知识。
第五节 二分搜索
1 顺序查找:
找到目标的第一个位置,如果找不到则返回-1;
程序
def bi_search_iter(alist, item):
left, right = 0, len(alist) - 1
while left <= right:
mid = (left + right) // 2
if alist[mid] < item:
left = mid + 1
elif alist[mid] > item:
right = mid - 1
else: # alist[mid] = item
return mid
return -1
num_list = [1,2,3,5,7,8,9]
print(bi_search_iter(num_list, 7))
print(bi_search_iter(num_list, 4))
输出结果

2 二分查找模板:
在刚开始学习写程序的时候,按照下面程序的思路体现四个重点内容,就可以解决百分之五十的二分查找难题;
程序
def binarysearch(alist, item):
# 第一个重点
if len(alist) == 0:
return -1 # 注意边界条件
# 在碰到类似的情况时,将边界条件程序写上去;对运行时间没有影响;
# 可以减少后续担心的情况;
left, right = 0, len(alist) - 1
# 第二个重点
while left + 1 < right: # 当L和R相邻的时候,当L和R相等、R小于L的时候,跳出循环体;
mid = left + (right - left) // 2
# 第三个重点
if alist[mid] == item:
right = mid # 找到的首次出现的目标元素的位置;
elif alist[mid] < item:
left = mid
elif alist[mid] > item:
right = mid
# 第四个重点
# 退出循环之后,需要进行兜底的判断;
# 当L和R相邻,当L和R相等的时候,L和R都可能等于2,所以将目标元素和L和R相比,因为找第一个位置,所以将L放在前面 ;兜底
if alist[left] == item:
return left
if alist[right] == item:
return right
return -1
3 在旋转有序数列中查找最小值
假设有一个升序排列的数列在某个未知节点处被前后调换,请找到数列中的最小值;
程序
# 方法1
def searchlazy(alist): #O(nlgn)
alist.sort() # 先排序
return alist[0]# 返回第一个元素
# 方法2
def searchslow(alist):#O(n)
mmin = alist[0]
for i in alist:
mmin = min(mmin, i)
return mmin
# 方法3
def search(alist):# O(lgn)
if len(alist) == 0:
return -1 # 第一个重点,先写边界条件
# 第二个重点
left, right = 0, len(alist) - 1
while left + 1 < right:
if (alist[left] < alist[right]):# 如果数据有序,未被旋转;
return alist[left];
# 第三个重点
mid = left + (right - left) // 2
if (alist[mid] >= alist[left]):# 前半部分有序,到后半部分去寻找
left = mid + 1
else:
right = mid # 到前半部分去找
# 第四个重点;兜底 L和R相邻,
return alist[left] if alist[left] < alist[right] else alist[right]
4 在旋转数组中查找
假设有一个升序排列的数列在某个未知节点处被前后调换,请找到目标值;
程序
#O(lgn)
def search(alist, target):
if len(alist) == 0: # 第一个重点:初始条件的判断
return -1
left, right = 0, len(alist) - 1
while left + 1 < right:
mid = left + (right - left) // 2
# 第二个重点:
if alist[mid] == target:
return mid
# 第三个重点:
if (alist[left] < alist[mid]):
if alist[left] <= target and target <= alist[mid]: # 判断target是否在前半部分
right = mid # 在前半部分寻找
else:
left = mid # 在后半部分寻找
else: #与上面相反
if alist[mid] <= target and target <= alist[right]:
left = mid
else:
right = mid
# 第四个重点:兜底程序
if alist[left] == target:
return left
if alist[right] == target:
return right
return -1
5 搜索插入位置
• 给定有序数组和一个目标值,如果在数组中找到此目标值则返回目标值的index,如果 没有找到,则返回目标值按顺序应该被插入的位置index.
• 注:可以假设数组中不存在重复数
程序
# 首先找到第一个大于等于target的数
def search_insert_position(alist, target):
if len(alist) == 0: # 第一个重点
return 0
left, right = 0, len(alist) - 1
while left + 1 < right: #第二个重点
mid = left + (right - left) // 2
if alist[mid] == target:
return mid
# 第三个重点
if (alist[mid] < target):
left = mid
else:
right = mid
# 第四个重点:兜底
if alist[left] >= target:
return left
if alist[right] >= target:
return right
# 当L和R都小于target ,插入在最后;
return right + 1
6 搜索区间
• 给一个有序、有重复数字的数组。找到给定目标值的开始和结束位置,如果目标数据不存在,返回(-1,-1)
思路
思路
首先运行找到第一个元素的程序,然后运行找到最后一个元素的程序;时间复杂度 O(lgn)
程序
# O(lgn)
def search_range(alist, target): # 第一个重点,base
if len(alist) == 0:
return (-1, -1)
lbound, rbound = -1, -1
# search for left bound
left, right = 0, len(alist) - 1
while left + 1 < right: # 第二个重点
mid = left + (right - left) // 2
if alist[mid] == target: # 第三个重点
right = mid
elif (alist[mid] < target):
left = mid
else:
right = mid
if alist[left] == target: # 第四个重点 兜底程序
lbound = left
elif alist[right] == target:
lbound = right
else:
return (-1, -1)
# search for right bound
left, right = 0, len(alist) - 1
while left + 1 < right:
mid = left + (right - left) // 2 # 第二个重点
if alist[mid] == target: # 第三个重点
left = mid
elif (alist[mid] < target):
left = mid
else:
right = mid
if alist[right] == target: # 第四个重点
rbound = right
elif alist[left] == target:
rbound = left
else:
return (-1, -1)
return (lbound, rbound)
7 在用空字符串隔的字符串的有序数列中查找
给定一个有序的字符串序列,这个序列中的字符串用空字符隔开,请写出找到给定字符串位置的方法;
思路
先从左往右或者从右往左找到非字符元素,然后再按照二分法,寻找mid,再将target和mid和寻找的非字符运输做比较,再决定mid向哪一端移动。
程序
# O(n) 可以用in逐项遍历
def search_empty(alist, target):
if len(alist) == 0:
return -1
left, right = 0, len(alist) - 1
while left + 1 < right:
while left + 1 < right and alist[right] == "": # 从右边开始找,找到第一个非空字符串,并将其位赋值给right
right -= 1
if alist[right] == "":
right -= 1
if right < left:
return -1
mid = left + (right - left) // 2
while alist[mid] == "": # 当中间是空字符串时,向后寻找;
mid += 1
if alist[mid] == target:
return mid
if alist[mid] < target:
left = mid + 1
else:
right = mid - 1
if alist[left] == target:
return left
if alist[right] == target:
return right
return -1
8 在无限序列中找到某元素的第一个出现位置
有序数据流
不知道序列长度
思路
先从左往右或者从右往左找到非字符元素,然后再按照二分法,寻找mid,再将target和mid和寻找的非字符运输做比较,再决定mid向哪一端移动。
程序
# 在有很多0的数组中找1出现的位置
def search_first(alist):
left, right = 0, 1
while alist[right] == 0:
left = right
right *= 2 # right变为2倍
if (right > len(alist)):
right = len(alist) - 1
break
return left + search_range(alist[left:right+1], 1)[0]
9 **供暖设备 **
• 冬季来临!你的首要任务是设计一款有固定供暖半径的供暖设备来给所有的房屋供 暖。
• 现在你知道所有房屋以及供暖设备在同一水平线上的位置分布,请找到能给所有房 屋供暖的供暖设备的最小供暖半径。
• 你的输入是每个房屋及每个供暖设备的位置,输出应该是供暖设备的最小半径
思路
转换为两个数组,寻找一个数组在另外一个数组中距离最近的值。
先将供暖设备的数组进行排序;
找到每个房屋左边和右边距离最近的供暖设备,再选出最近的距离和对应的设备。
在所有房屋的最近距离的最大值。
程序
from bisect import bisect
def findRadius(houses, heaters):
heaters.sort() #对设备进行排序
ans = 0
for h in houses:
hi = bisect(heaters, h)# bisect:找到heaters第一个大于等于h的位置,也是h应该在heaters插入的位置,但是不插入
left = heaters[hi-1] if hi - 1 >= 0 else float('-inf') # 查找左边最近的设备的位置
right = heaters[hi] if hi < len(heaters) else float('inf') # 查找右边最近设备的位置
ans = max(ans, min(h - left, right - h)) # 返回所有距离最小值得最大值
return ans
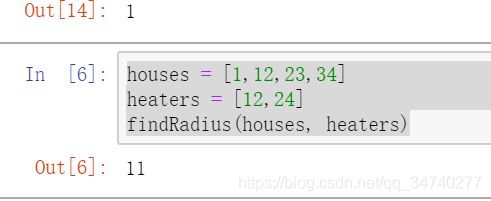
houses = [1,12,23,34]
heaters = [12,24]
findRadius(houses, heaters)
输出结果
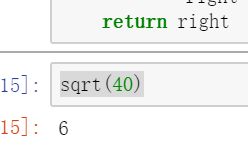
10 sqrt(x)
计算并返回x的平方根。x保证是一个非负整数。
程序
方法1
# 二分查找法
def sqrt(x):
if x == 0:
return 0
left, right = 1, x
while left <= right:
mid = left + (right - left) // 2
if (mid == x // mid):
return mid
if (mid < x // mid):
left = mid + 1
else:
right = mid - 1
return right
sqrt(40)
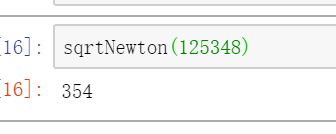
def sqrtNewton(x):
r = x
while r*r > x:
r = (r + x//r) // 2
return r
sqrtNewton(125348)
输出结果
11 矩阵搜索
在一个MN的矩阵里,每一行都是排好序的,每一列也是排好序的,请设计一个算法在矩阵中查找一个数。
思路
1、依次遍历矩阵中的数组; O(MN)
2、在每一行(列)分别采用二分法查找;min(nlgm、mlgn)
3、因为矩阵的每一行每一列都是排好序的,所有每个元素都大于其左边和上面的元素,小于右边和下面的元素;但是对于边界元素,当元素和其相比之后,根据相比的结果就只有一个方向进行移动。
程序
**12 矩阵搜索 II **
在一个MN的矩阵里,每一行都是排好序的,每一列也是排好序的,请设计一个算法在矩阵中查找第K大的数。
思路
1、依次遍历矩阵中的数组; O(MN)
2、在每一行(列)分别采用二分法查找;min(nlgm、mlgn)
3、因为矩阵的每一行每一列都是排好序的,所有每个元素都大于其左边和上面的元素,小于右边和下面的元素;但是对于边界元素,当元素和其相比之后,根据相比的结果就只有一个方向进行移动。
**13 找到重复数 **
给定一个包含n+1个整数的数组,其中每个元素为1到n闭区间的整数值,请证明至少 存在一个重复数。假设只有一个重复数,请找到这个重复数。
要求:
1、不能太慢;
2、不给排序;
3、不准用set!
4、不准对原数据进行修改;
思路
数据的范围为1到n,找到中间值m,将所有的数字和m比较,从而得知多少数字小于m多少大于m,然后可以判断出重复的数字在前面还是后边。如果在前面,再找出1到m的中间值m1,如果在前面,再找出m到n的中间值m2,依次类推,就能找到重复数;
时间复杂度:nlogn;
程序
# O(nlogn)
def findDuplicate(nums):
low = 1
high = len(nums)-1
while low < high: # 大循环
mid = low + (high - low) // 2
count = 0
for i in nums: # 找到中间值m,将所有的数字和m比较。
if i <= mid:
count+=1
if count <= mid:
low = mid+1
else:
high = mid
return low
nums = [3,5,6,3,1,4,2]
findDuplicate(nums)
输出结果

14 地板和鸡蛋
假设有一个100层高的建筑,如果一个鸡蛋从第N层或者高于N层坠落,会摔破。如果 鸡蛋从任何低于N层的楼层坠落,则不会破。现在给你2个鸡蛋,请在摔破最少鸡蛋 的情况下找到N。
思路
第一个鸡蛋找出范围。第二个鸡蛋精确定位;
为充分利用鸡蛋和平均分配;
①如果第1个鸡蛋在第k层摔破了,第二个鸡蛋就可以从第1层开始慢慢测试,最多k次可以测试到准确楼层;
②如果第1个鸡蛋在k层没有摔破,这个时候就只剩下k-1次机会了,第2次测试的时候第1个鸡蛋就可以在第k+(k-1)层测试。如果第2次第1个鸡蛋摔破了,第2个鸡蛋就可以从k层开始慢慢的往k+(k-1)层测试,如果没有摔破,就继续同样的往更高层测试,第三次的话就应该是k+(k-1)+(k-2)层测试了,这样就可以确保剩下的机会可以准确测试到摔破的楼层。
③所以公式是:k+(k-1)+(k-2)+…+1>=100;转化一下就是:k(k+1)/2>=100;求解k>=14;所以100层楼最少14次可以测试到准确摔破楼层;
15 找到两个有序数组的中值
给定两个长度分别为N1和N2的有序数组,请用时间复杂度为 O(log N) 的方法找到所 有元素的中值,这里N=N1+N2。。
思路
16 合并区间
• 给定一个区间的集合,将所有存在交叉范围的区间进行合并。
• 输入: [[1,3],[2,6],[8,10],[15,18]]
• 输出: [[1,6],[8,10],[15,18]]
• 说明: 因为区间 [1,3] 和 [2,6] 存在交叉范围, 所以将他们合并为[1,6].
思路
首先根据每个区间的起始时间进行排序;得到三种结果:每个区间首尾都没有交叉、区间之间有交叉、区间之间有包含;对于区间有交叉和包含的情况,新区间的开始时间为开始时间的最小值,结束时间为结束时间的最大值;
程序
class Interval:
def __init__(self, s=0, e=0):
self.start = s
self.end = e
def __str__(self):
return "[" + self.start + "," + self.end + "]"
def __repr__(self):
return "[%s, %s]" % (self.start, self.end)
def merge(intervals):
intervals.sort(key=lambda x: x.start) # 对所有的起始时间进行排序
merged = []
for interval in intervals:
# if the list of merged intervals is empty or if the current
# interval does not overlap with the previous, simply append it.
if not merged or merged[-1].end < interval.start:
merged.append(interval)# 这种情况说明没有交叉
else:
# otherwise, there is overlap, so we merge the current and previous
# intervals.
merged[-1].end = max(merged[-1].end, interval.end) # 该种情况说明有交叉,需要合并
return merged
i1 = Interval(1,3)
i2 = Interval(2,6)
i3 = Interval(8,10)
i4 = Interval(15,18)
intervals = [i1,i2,i3,i4]
print(merge(intervals))
输出结果

17 插入区间
• 给定一个没有交叉范围的区间集合,在这个集合中插入一个新的区间(如果需要,请进行合并)。
• 你可以认为这些区间已经初始时根据他们的头元素进行过排序
• 输入:区间集合=[[1,3],[6,9]], 新区间 = [2,5]
• 输出:[[1,5],[6,9]]
思路
先插入区间;再合并;
新进入的区间有三种情况;和原有区间没有交叉,和原有区间有交叉;
对于有交叉的情况,先合并,再输出;
程序
def insert(intervals, newInterval):
merged = []
for i in intervals:
if newInterval is None or i.end < newInterval.start:
merged += i,
elif i.start > newInterval.end:
merged += newInterval,
merged += i,
newInterval = None
else:
newInterval.start = min(newInterval.start, i.start)
newInterval.end = max(newInterval.end, i.end)
if newInterval is not None:
merged += newInterval,
return merged
i1 = Interval(1,3)
i2 = Interval(6,9)
intervals = [i1,i2]
new = Interval(2,5)
insert(intervals, new)