数据结构与算法学习笔记(python)——第三节 递归
前言
本人是一个长期的数据分析爱好者,最近半年的时间的在网上学习了很多关于python、数据分析、数据挖掘以及项目管理相关的课程和知识,但是在学习的过程中,过于追求课程数量的增长,长时间关注于学习了多少多少门课程。事实上,学完一门课之后真正掌握的知识并不多,主要的原因是自己没有认真学习和理解温故而知新的这句话的真正含义。因此,从现在开始,我在学习《数据结构与算法——基于python》的课程内容之后,抽出固定的时间对每天学习的内容进行总结和分享,一方面有助于个人更好的掌握课程的内容,另一方面能和大家一起分享个人的学习历程和相应的学习知识。
第三节 递归
## 基础知识:
3.1 递归函数是一种自我调用的函数。
递归的两个必要条件:基础条件、F(n)和F(n-1) 的关系;
递归程序一般需要的时间复杂度和空间复杂度都比较大,但是对于for循环不适合的程序,就需要用递归来完成;
在python中定义了一个递归的最大深度,当递归深度超过定义的之后,递归算法将不再适用;
递归应用:
- *Simple Example 求和
传统方式
n = 10
result = sum(range(n+1))
result
或者
def mysum(n):
result = 0
for i in range(n+1):
result += i
return result
result = mysum(10)
result
递归方法
def mysum_recursive(n):
if n == 0:
return 0
return n + mysum_recursive(n-1)
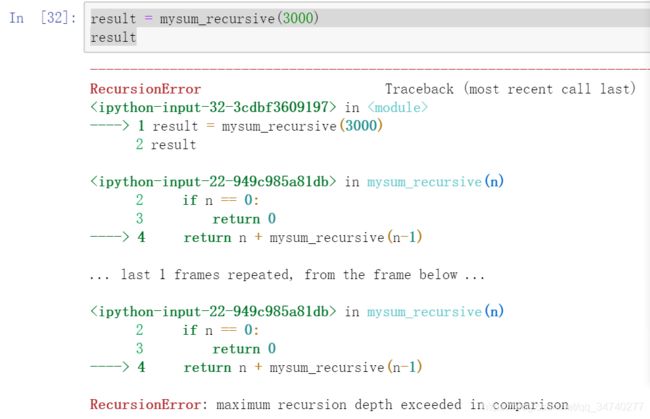
result = mysum_recursive(300)
result
当递归运算的次数太多,超过python规定的递归深度之后,程序就会报错;
2. *Ex.2 阶乘
传统方式
def factorial(n):
result = 1
for i in range(1, n+1):
result *= i
return result
factorial(5)
递归方法
def factorial_recursive(n):
if n == 1:
return 1
return n * factorial_recursive(n - 1)
factorial_recursive(5)
- *Ex.3 斐波那契数
方法1
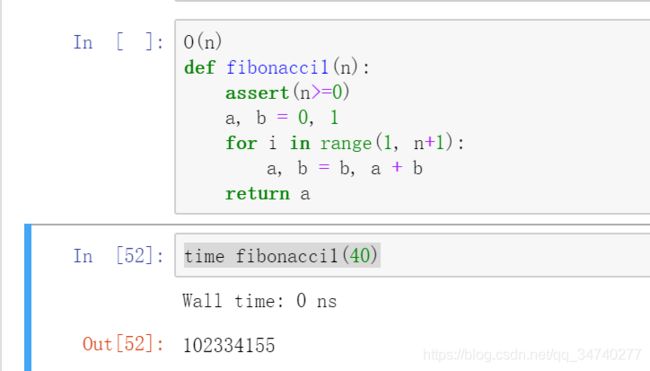
O(n)
def fibonacci1(n):
assert(n>=0)
a, b = 0, 1
for i in range(1, n+1):
a, b = b, a + b
return a
time fibonacci1(40)
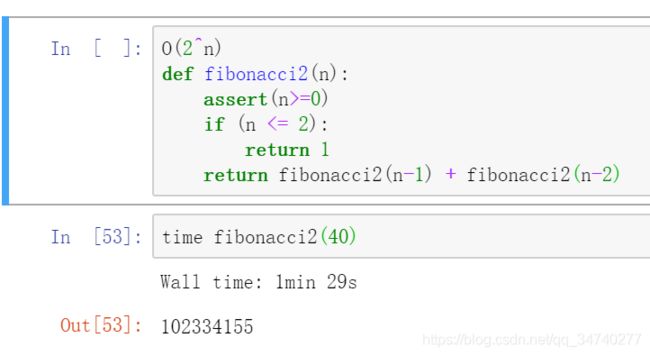
O(2^n)
def fibonacci2(n):
assert(n>=0)
if (n <= 2):
return 1
return fibonacci2(n-1) + fibonacci2(n-2)
time fibonacci2(40)
def fibonacci3(n):
assert(n>=0)
if (n <= 1):
return (n,0)
(a, b) = fibonacci3(n-1)
return (a+b, a)
time fibonacci3(40)

通过上述三个不同方法之间的对比,从输出结果都是一致且是正确的,但是从时间复杂度上来讲,三种方法中,方法1最快,方法2其次,方法3最慢,我敲完这段话至少两分钟的时间,还没有算出来!
为什么要计算斐波那契数列呢
计算一下每一项和前一项之间的比例;
def fibonaccis(n):
assert(n>=0)
result = [0, 1]
for i in range(2, n+1):
result.append(result[-2] + result[-1])
return result
fibos = fibonaccis(30)
r = []
for i in range(2, len(fibos)):
r.append(fibos[i] / fibos[i-1])
r
输出结果,当数据运行的越来越大之后,两项之比都接近一个固定的数字,1.618,这是我们所说的黄金比例;

事实上,自然界中很多的生物都具有黄金比例,肚脐到脚的距离/身高=0.618


4. Ex.4 画尺子
先输出如下所示的数字串
1
1 2 1
1 2 1 3 1 2 1
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
思路
根据上述情况可以看出,数据是一个递归的状态;第n项等于第n-1项+n + 第n-1项;根据上述思路,可以写出如下的三种代码;
代码
# O(2^n)
def ruler_bad(n):
assert(n>=0)
if (n==1):
return "1"
return ruler(n-1) + " " + str(n) + " " + ruler(n-1)
# O(n) 将前一个计算结果存储起来,减少重复计算,降低时间复杂度
def ruler(n):
assert(n>=0)
if (n==1):
return "1"
t = ruler(n-1)
return t + " " + str(n) + " " + t
# O(n) 用for 循环的方式
def ruler2(n):
result = ""
for i in range(1, n+1):
result = result + str(i) + " " + result
return result
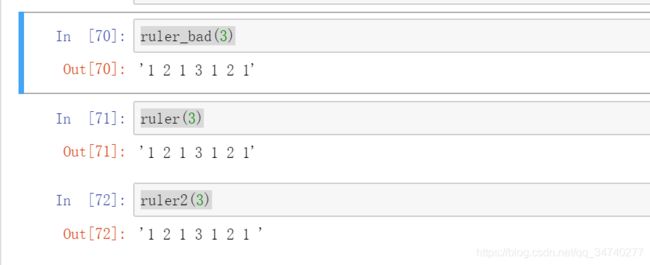
ruler_bad(3)
ruler(3)
ruler2(3)
输出结果
根据上述思路可以写出如下图所示的尺子的递归程序;
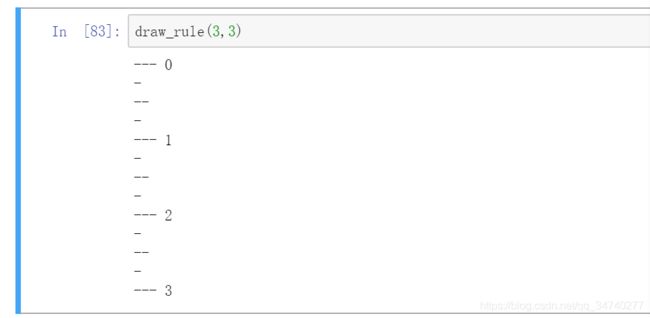
代码
def draw_line(tick_length, tick_label=''):# 画中间的最高线
line = '-' * tick_length
if tick_label:
line += ' ' + tick_label
print(line)
def draw_interval(center_length): # 画中间的刻度
if center_length > 0:
draw_interval(center_length - 1)
draw_line(center_length)
draw_interval(center_length - 1)
def draw_rule(num_inches, major_length): # 画尺子程序
draw_line(major_length, '0')
for j in range(1, 1 + num_inches):
draw_interval(major_length - 1)
draw_line(major_length, str(j))
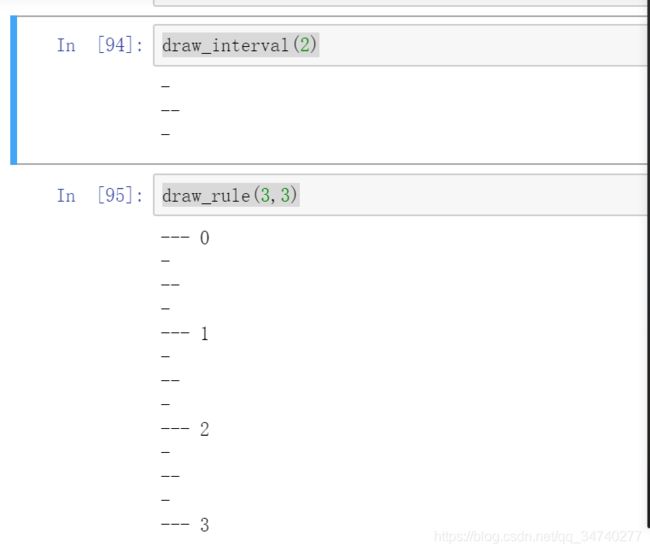
draw_interval(2)
draw_rule(3,3)
输出结果
5. Ex.5 数学表达式
给定两个等于a≤b的整数,编写一个程序,以最小的递增(加1)和展开(乘以2)操作序列将a转换为b。
例如,
23 =((5 * 2 +1)* 2 +1)
113 =(((((11 +1)+1)+1)* 2 * 2 * 2 +1)
思路
根据题目要求,a≤b,且只能用+1,和X2的操作,使算式相等。可分为以下三种情况;
1、b<2a, 只能做加法
2、b<2a,将a乘以2,然后再做加1;
3、b=2a,或者b=a,这是两种基础情况;
根据第1、2 两种情况判断是做+1还是X2的操作。再判断奇偶性。
按照上述思路,可以写出如下代码;
def intSeq(a, b):
if (a == b): # base
return str(a)
if (b % 2 == 1): # 说明b是一个奇数,可先将b变成b-1,求得b-1和a的关系,再+1
return "(" + intSeq(a, b-1) + " + 1)"
# b是偶数的情况
if (b < a * 2): # 如果b<2a,只能一个一个做+1操作。
return "(" + intSeq(a, b-1) + " + 1)"
# 剩下的情况就是b>2a,且b为偶数。
return intSeq(a, b/2) + " * 2";
a = 5;
b = 101;
print(str(b) + " = " + intSeq(a, b))
输出结果如下所示;
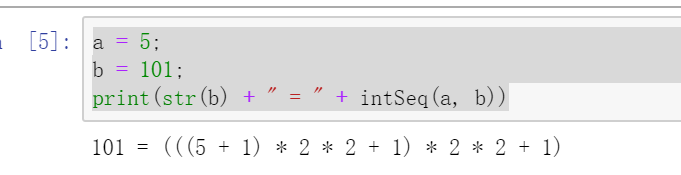
6. Ex.6 汉诺塔问题
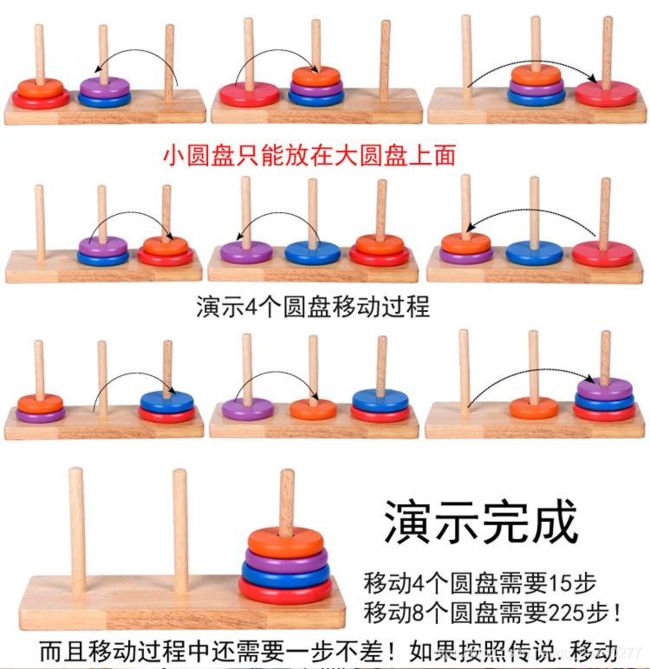
思路
根据规则要求,可以自己推断出3阶汉诺塔需要7步,四阶汉诺塔需要15步,5阶需要31步,可以分析出规律。f(n)=2^n-1次;需要程序输出每一步移动的过程,说明从哪儿到哪儿。
对于三界汉诺塔,需要下列的步骤;
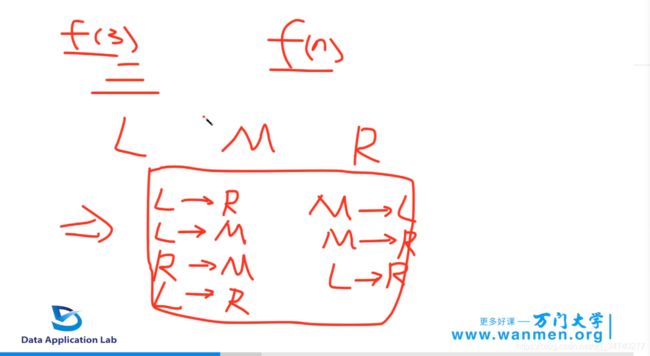
同时需要输出f(n)的步骤,根据递归思想。
base: f(1)就是L到R;
递归:f(n),假设知道f(n)的答案,推导f(n+1)。f(n)和f(n+1)之间的关系如下图所示;
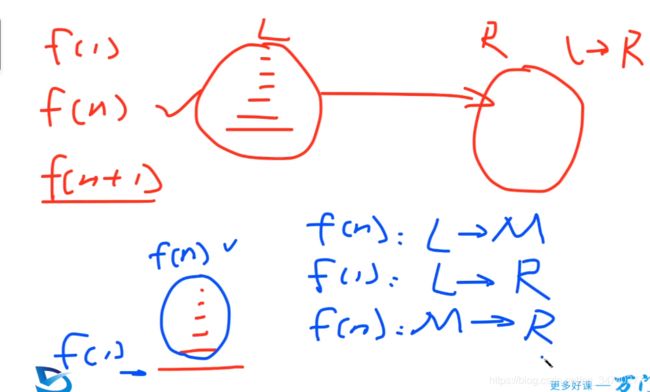
由于需要表明移动的位置,应该在函数中定义初始位置,中间位置,末尾位置;
按照上述思路,可以写出如下代码;
def hanoi(n, start, end, by):
if (n==1):
print("Move from " + start + " to " + end)
else:
hanoi(n-1, start, by, end)
hanoi(1, start, end, by)
hanoi(n-1, by, end, start)
n = 3
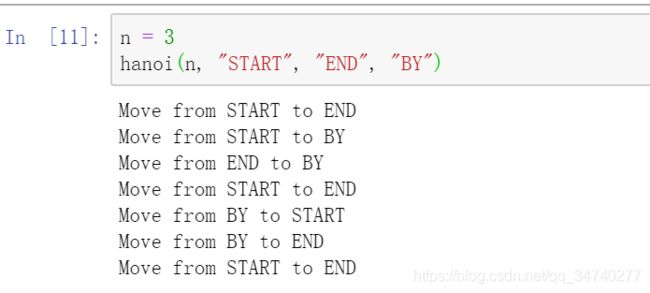
hanoi(n, "START", "END", "BY")
输出结果;
7. Ex.7 格雷码

每一次和上一次有一个数字是不一样的,0000变为0001,按照这样的规律改变;
给定两个等于a≤b的整数,编写一个程序,以最小的递增(加1)和展开(乘以2)操作序列将a转换为b。当第i个位置由0变成1之后,表示为enter i,由1变成0之后,表示为exit i,再进行enter 操作,如此循环。
思路:
通过图片中的move 那一列的数据:121312141213121,和前面的画尺子那道题是类似的,对于121312141213121中,每一个数字第一次出现的时候,是enter。第二次出现之后变成exit,然后不再变化。
f(1)的时候,enter 1;f(2)的时候,enter 1,enter 2,exit 1;f(3)的时候,enter 1,enter 2,exit 1,enter 3,enter 1,exit 2,exit 1;首先得有enter,然后再有exit。先enter,然后调用下一级的code,enter 1,然后调用本身自己的exit,enter 自己,enter 下一级,exit 自己。
按照上述思路;可以写出如下程序;
程序
def moves_ins(n, forward): # forward 的不同的值来表示输出enter 还是exit
if n == 0:
return
moves_ins(n-1, True)
print("enter ", n) if forward else print("exit ", n)
moves_ins(n-1, False)
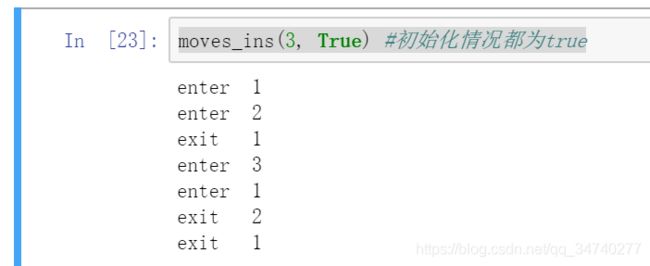
moves_ins(3, True) #初始化情况都为true
输出结果!
8. Ex.8 子集
子集的定义:子集是一个数学概念,如果集合A的任意一个元素都是集合B的元素(任意a∈A则a∈B),那么集合A称为集合B的子集。
在n个元素中,对于每个元素,存在两种状态,选择或者不选择,因此,对于含有n个元素的集合,共有2^n个子集。编写一个程序,输出该集合的所有子集。
对于含有a、b、c三个元素的集合;首先取出空集,成为一个子集,对于a,先取出来,然后空集加上a,得到两个子集,空集和a。对于b,把之前的两个集合加上b,空集中加上b,a里面加上b,形成了四个集合,然后对于c,将c分别加到上述四个集合里面,形成了4个新的子集,一共形成了8个子集。具体如下图所示;
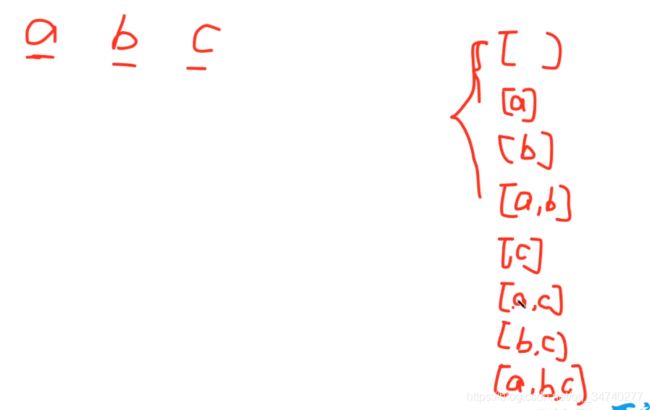
根据上述思路,可以写出如下的程序。
def subsets(nums):
result = [[]] # 一个二维数组
for num in nums:
for element in result[:]: # 建立一个result的copy 不能在原始数据上进行操作
x=element[:] # 建立一个element的copy 不能在原始数据上进行操作
x.append(num)
result.append(x)
return result
nums = [1, 2, 3]
print(subsets(nums))
输出结果;

根据输出结果,可以判定该程序是正确的。
留下两个问题:
1、 result[:] 这里为什么要make a copy
2、element[:] 这里为什么要make a copy
另外一种方法:
具有通用性,对于其他语言也可以按照这种方式;
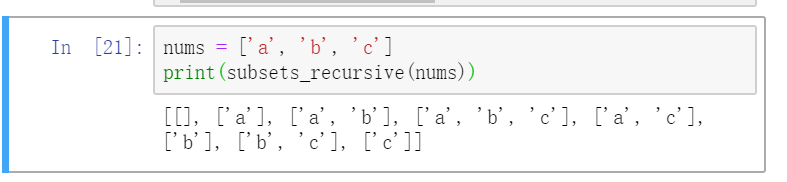
还是用之前a、b、c的三个例子,构建一个搜索树;
刚开始有一个空集,对于a,如果使用了a,b和c还没有使用,可以得到一个a。继续使用b,得到ab,在ab的基础上,考虑c,得到abc。使用c,得到ac;得到 空集、a、ab、abc、ac这五种选项,这时,a这条路走完了。对于b这条搜索路,可以得到b、bc这两种。对于c这个搜索树,得到c;一共得到了8个子集;
在上述过程中,如果路走不通了,就往回走,和深度搜索一样,在往回追溯的过程中,应当恢复到第一次访问的状态,如下图所示;
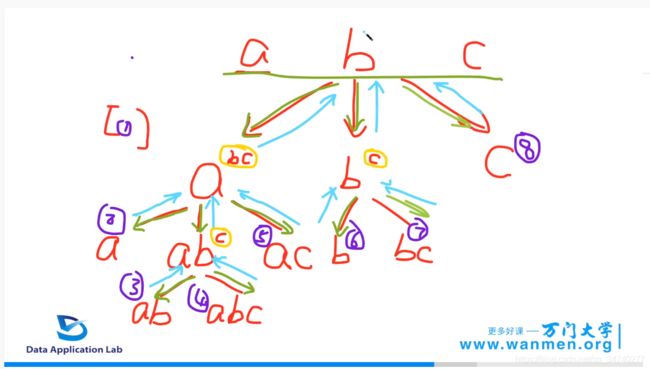
按照上述思路可以写出下列程序;
# 最好能把这个程序背下来,面试被抽到的几率很大
def subsets_recursive(nums):
lst = [] # 初始化一个空集
result = [] # 最好返回的结果,将list放入result里面
# helper 辅助性的函数。
subsets_recursive_helper(result, lst, nums, 0);
return result;
def subsets_recursive_helper(result, lst, nums, pos):
result.append(lst[:]) # 先将result加进来,create了一个list_copy
for i in range(pos, len(nums)): #考察未被放入的元素,刚开始将a放进去;
lst.append(nums[i])
subsets_recursive_helper(result, lst, nums, i+1) # a放进去之后,不用再加入a了,所有pos需要+1操作,
# 等所有的元素都进入到result里面之后,开始回溯,回溯的要求是和第一次访问的状态相同,此时是abc,应该将c去掉,变成ab,
lst.pop() # c在最上面,进行出栈操作,ab也已经出现了。继续出栈,变成a,继续探索ac
nums = ['a', 'b', 'c']
print(subsets_recursive(nums))
程序结合图片理解更好!
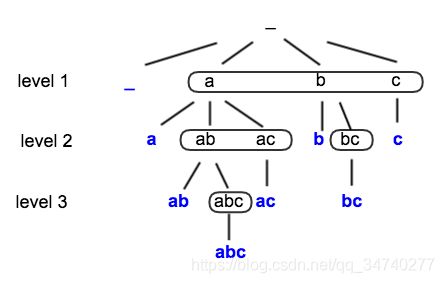
输出结果;
9. **Ex.2 子集 II **
给定一组可能包含重复项的整数,则返回所有可能的子集,返回子集的集合里面,不能有重复的元素。
思路
对于 a、b、b,建立一个数组,当a[n]= a[n-1]的时候,可以认为该元素已经出现过,和上面的例子相比,增加一个排序的功能,a[n]= a[n-1]的时候,就跳出循环。
根据上述思路;可以写成如下程序;
def subsets_recursive2(nums):
lst = []
result = []
nums.sort() #对input进行排序。
#print(nums)
subsets2_recursive_helper(result, lst, nums, 0);
return result;
def subsets2_recursive_helper(result, lst, nums, pos):
result.append(lst[:])
for i in range(pos, len(nums)):
if (i != pos and nums[i] == nums[i-1]):
continue; # 当前的数字和之前的数字相等时,跳出此次循环
lst.append(nums[i])
subsets2_recursive_helper(result, lst, nums, i+1)
lst.pop()
nums = [1, 2, 3])
print(subsets_recursive2(nums))
- **Ex.10 排列组合 **
Given abc:
Output: bca cba cab acb bac abc
输出n个集合的所有的排列组合,n个元素共有n的阶乘个子集。
思路
对于 a、b、c,首先搜索a,然后剩下b和c,可以选择b,接着选择c,变成abc,此时没有其他选择了。先选择,或者先选择c,按照和a同样的规则即可。
按照上述思路,可以写出一下程序;
def perm(result, nums):
if (len(nums)==0): # 当数组大小为零时(nums为空,表示所有的元素已经排列完),就将数组打印出来。
print(result)
for i in range(len(nums)):
perm(result+str(nums[i]), nums[0:i]+nums[i+1:]) # nums[0:i]+nums[i+1:] 表示除第i个元素后剩余的元素。
nums = [1, 2, 3]
perm('', nums)
输出结果
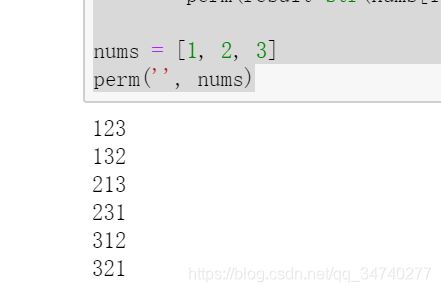
11. **Ex.11 唯一排列组合 **
输出n个集合的所有的唯一的排列组合,n个元素共有n的阶乘个子集,
思路
和唯一子集中的元素方法详细,先对每个元素进行排序,然后对已经操作过的元素不在进行操作。根据此思路,得出的代码如下;
代码
def permUnique(result, nums):
nums.sort() # 首先进行排序
if (len(nums)==0):
print(result)
for i in range(len(nums)):
if (i != 0 and nums[i] == nums[i-1]):
continue; # 对于重复的元素,进行剪枝,已经出现的元素不再进行操作。
permUnique(result+str(nums[i]), nums[0:i]+nums[i+1:])
nums = [1, 2, 3]
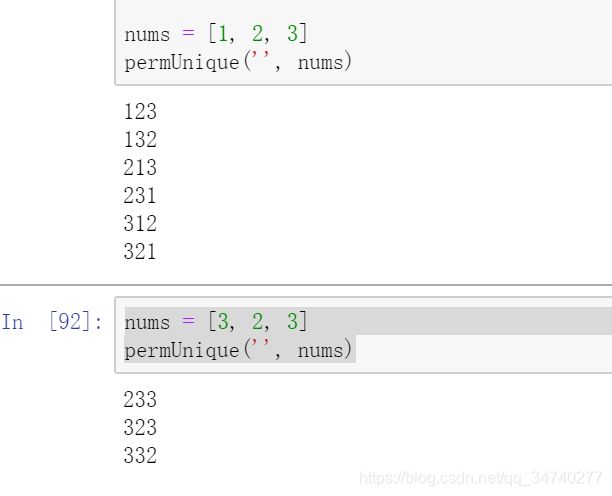
permUnique('', nums)
nums = [3, 2, 3]
permUnique('', nums)
对比运行结果;对于3,2,3.这个集合没有输出重复的子集。
12. **Ex.12 K个元素的排列组合 **
取两个参数n和k,并打印出所有P(n,k)= n! /(n-k)! 恰好包含n个元素中的k个的排列。 当k = 2且n = 4时。
ab ac ad ba bc bd ca cb cd da db dc
思路
和子集一样的思路,只是当k=0 的时候选择结束,表示里面的元素已经够两个了;
代码
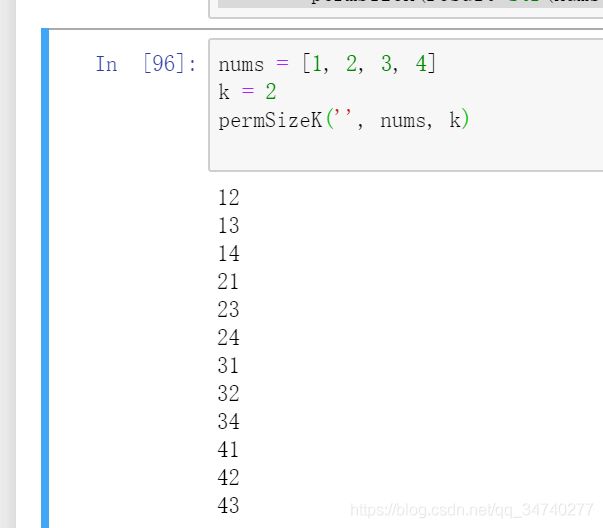
def permSizeK(result, nums, k):
if k == 0: # 当k=0时,表示已经选出了讲个元素。
print(result)
for i in range(len(nums)):
permSizeK(result+str(nums[i]), nums[0:i] + nums[i+1:], k - 1)
nums = [1, 2, 3, 4]
k = 2
permSizeK('', nums, k)
输出结果
13. **Ex.13 字母大小写排序 **
枚举输入中指定的任何字母的所有大写/小写排列;
For example,
word = “medium-one”
Rule = “io” i和o都有大写和小写,然后做一个排列组合
solutions = [“medium-one”, “medIum-one”, “medium-One”, “medIum-One”]
14 Ex.14 组合总和
给定一组候选编号(候选)(无重复)和目标编号(目标),在候选编号总和为目标的候选中找到所有唯一组合。在一个数组中间,找到一个子集,使得子集的和目标值相等。
可以从候选人无限制的次数中选择相同的重复数。
思路
base:每次找到一个数字之后,用目标值减掉这个数字,剩余的数值是下面要搜索的路径。当剩余值为零的时候,就找到了。
剩下的思路和寻找子集题目的思路一致,根据上述思路可以写出下列程序。
代码
def comb(nums, t):
result = []
tmp = []
combHelper(result, tmp, nums, t, 0)
return result
def combHelper(result, tmp, nums, remains, start):
if remains < 0: return
if remains == 0: # 当remains为零的时候,表示结束
result.append(tmp[:])
else:
for i in range(start, len(nums)):
tmp.append(nums[i])
combHelper(result, tmp, nums, remains - nums[i], i)
tmp.pop()
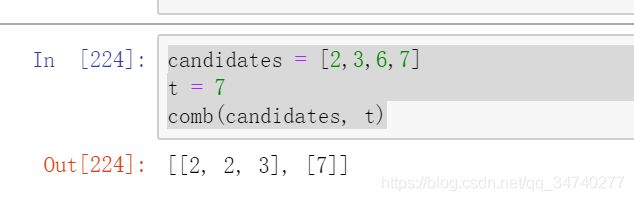
candidates = [2,3,6,7]
t = 7
comb(candidates, t)
输出结果
14 Ex.14 组合总和 II
给定候选编号(候选)和目标编号(目标)的集合,找到候选编号总和为目标的候选中的所有唯一组合。
候选中的每个数字在组合中只能使用一次。
注意:
所有数字(包括目标)将为正整数。
解决方案集不得包含重复的组合。
思路
在上一题的基础上加了一个唯一值的限制,和前面的唯一值的思路一样。先对元素进行排序,然后对于当前值和前面的值相等的直接跳过循环。
代码
def comb2(nums, t):
result = []
tmp = []
nums.sort() # 先排序
combHelper2(result, tmp, nums, t, 0)
return result
def combHelper2(result, tmp, nums, remains, start):
if remains < 0: return
if remains == 0:
result.append(tmp[:])
else:
for i in range(start, len(nums)):
if(i > start and nums[i] == nums[i-1]): continue; # skip duplicates 对于相同的直接跳过
tmp.append(nums[i])
combHelper2(result, tmp, nums, remains - nums[i], i + 1)
tmp.pop()
candidates = [10,1,2,7,6,1,5]
t = 3
comb2(candidates, t)
对比输出结果,根据输出结果,可以看出,可以当加unique的限制之后,结果中没有出现两个连续的相同的结果;
15 Ex.15 括号
给定n对括号,编写一个函数以生成格式正确的括号的所有组合。
思路
何谓好的括号配对,首先出现左括号,一共n对括号,有n个左括号和n个右括号,当用了一个左括号之后,还剩下n-1个左括号,n个右括号。
再打一个左括号,剩下n-2个左括号,n个右括号,可以打印完n个左括号,然后再打印n个右括号。
每一次先使用左括号;
具体过程如下图所示;
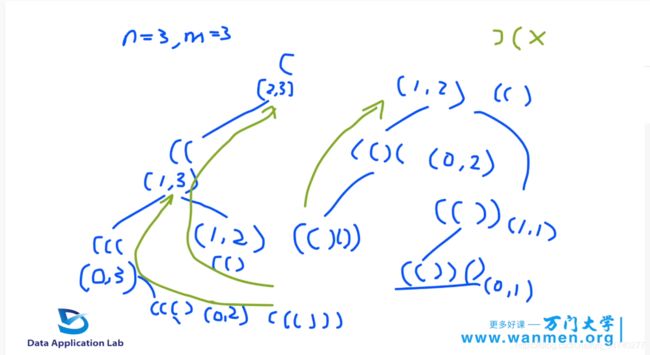
根据上述思路写出以下程序;
# str 不需要进行pop操作
# list 需要进行pop操作
def generateParenthesis(n):
def generate(prefix, left, right, parens=[]):
if right == 0: parens.append(prefix) #当右括号用完了,说明左括号也用完了。此时加到结果集里面去。
if left > 0: generate(prefix + '(', left-1, right)# 当左括号还有的时候,继续递归调用,
if right > left: generate(prefix + ')', left, right-1)# 当右括号大于左括号之后,说明左括号用完,上一条路已经走完,加上右括号,右括号数量减一。
return parens
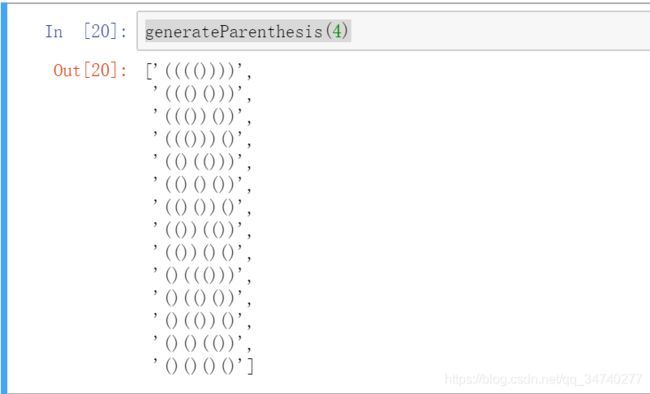
return generate('', n, n)
generateParenthesis(4)