一元线性回归利用最小二乘法求解原理代码及案例

1、线性回归的原理

基础定义

线性回归是利用数理统计中的回归分析，来确定两种或两种以上属性间相互依赖的定量关系的一种统计分析方法。举个例子，一套房子的具有面积、卧室数量、卫生间数量等三个属性，该房子的售价与上述三个属性息息相关，可以根据实际情况构造出各个属性之间的线性关系表达式，表达式就被成为线性回归方程；

房屋价格 = 0.8500 * 面积 + 0.0500 * 卧室数量 + 0.0015 * 卫生间数量

在实际生活中，我们可以获取多套房屋的面积、卧室数量、卫生间数量、售价等数据的值，根据历史数据，可以构造出属性之间更接近实际情况的线性数量关系表达式，利用线性回归方法对未出售的房屋售价进行预测。

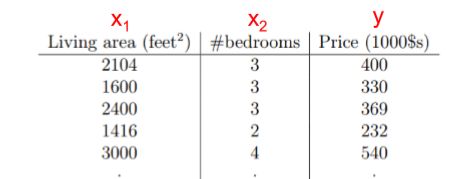
根据上述的历史数据，可以构造出一个简单的线性关系表达式：

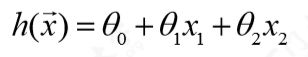
这个方程称为回归方程， θ1和θ2称为回X1和X2归系数或权重。预测的Y值需要尽可能的接近于接近于实际情况，为了衡量h(x)有多“接近”y，定义损失函数（cost function）:

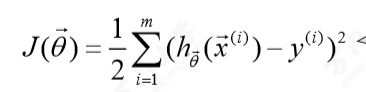
上述方程成为最小二乘损失函数，y(i)表示第i个训练实例对应的目标变量值，m为房屋的数量；常数1/2是为了方便后续计算；最小二乘法其实又叫最小平方法。

公式推导

对于一元线性回归来说，根据已知X和Y值，我们可以在坐标轴上面描出所有的点，找出一条直线，使这条直线“最贴近”已知的数据点，设此直线方程为：

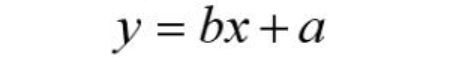
上述方程叫做Y对x的回归直线方程，b叫做回归系数。要想确定回归直线方程，我们只需确定a与回归系数b即可。
该方程预测出来的y值和实际的值差别越小越好，只有如此才能使直线最贴近已知点。我们求回归直线方程的过程其实就是求差别最小值的过程。
一个很自然的想法是把各个差加起来作为总差。可是，由于差有正有负，直接相加会互相抵消， 一般做法是我们用差的平方和，即：

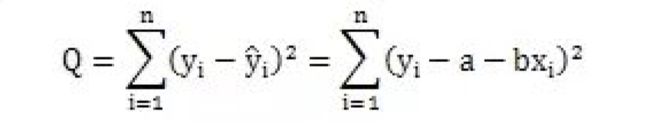
Q作为总差 ，并使之达到最小。这样回归直线就是所有直线中Q取最小值的那一条。由于平方又叫二乘方，所以这种使“离差平方和为最小”的方法，叫做最小二乘法。分别对a ,b 求导数，然后又令偏导数为0，可以得到最小二乘法求回归直线方程中的a、b的公式如下：

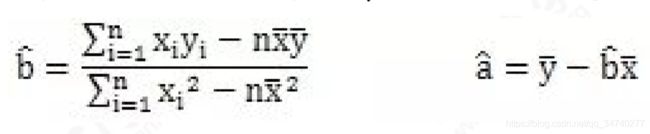
简单理解

小王跑运输的，跑1公里需要6块，跑2公里需要5块（那段时间刚好油价跌了），跑3公里需要7块，跑4 公里需要10块，请问跑5公里需要多少块？ 这里假定x是公里数，y是运输成本（β1和β2是要求的系数）。我们把上面的一组数据代入得到这么几个方程：

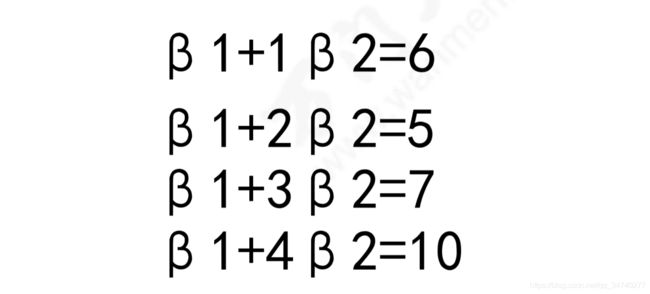
如果存在这样的β1和β2，让所有的数据（x，y）=（1,6），（2,5），（3,7），（4，10）都能满足 的话，那么解答就很简单了。找不到一条直线，穿过所有的点，因为他们不在一条直线上。希望找到一条直线，虽然不能满足所有 条件，但能近似地表示这个趋势，或者说，能近似地知道5公里的运输成本。

2、最小二乘法PYTHON实现

0. 导入相关库

import numpy as np
import matplotlib.pyplot as plt

1. 导入数据

points = np.genfromtxt('data.csv', delimiter=',') #生成points数组

points[0,0]

# 提取points中的两列数据，分别作为x，y
x = points[:, 0]# 第一列
y = points[:, 1]# 第二列

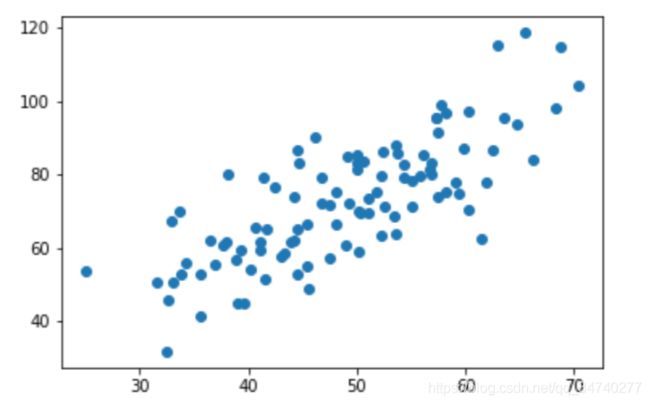
# 用plt画出散点图
plt.scatter(x, y)
plt.show()

2. 定义损失函数

# 损失函数是系数的函数，另外还要传入数据的x，y
def compute_cost(b, a, points):
    total_cost = 0
    N = len(points)
    
    # 逐点计算平方损失误差，然后求平均数
    for i in range(N):
        x = points[i, 0]
        y = points[i, 1]
        total_cost += ( y - b * x - a ) ** 2  
        
    return total_cost/N   

3. 定义算法拟合函数

# 先定义一个求均值的函数
def average(data):
    sum = 0
    num = len(data)
    for i in range(num):
        sum += data[i]
    return sum/num

# 定义核心拟合函数，拟合的过程就是用算法求b,a 的过程
def fit(points):
    N = len(points)
    x_bar = average(points[:, 0])
    
    sum_yx = 0
    sum_x2 = 0
    sum_delta = 0
    
    for i in range(N):
        x = points[i, 0]
        y = points[i, 1]
        sum_yx += y * ( x - x_bar )
        sum_x2 += x ** 2
    # 根据公式计算w
    b = sum_yx / ( sum_x2 - N * (x_bar**2) )  #根据公式10-1 w是b ,b是a
    
    for i in range(N):
        x = points[i, 0]
        y = points[i, 1]
        sum_delta += ( y - b * x )
    a = sum_delta / N
    
    return b, a

4. 测试定义的函数

b, a = fit(points)

print("b 是: ", b)
print("a 是: ", a)

cost = compute_cost(b, a, points)

print("cost 是: ", cost)

输出结果：

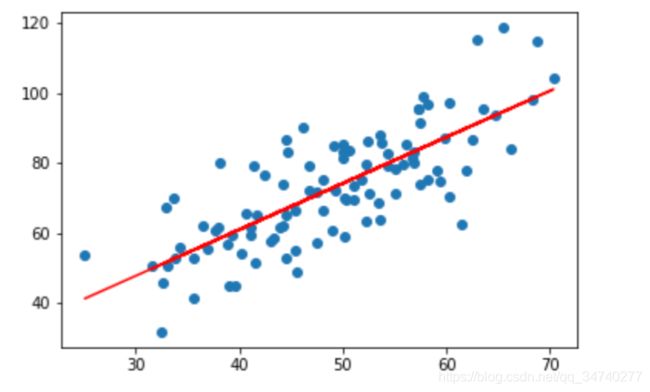
5. 画出拟合曲线

plt.scatter(x, y)
# 针对每一个x，计算出预测的y值
pred_y = b * x + a

plt.plot(x, pred_y, c='r')
plt.show()

3、最小二乘简单例子

##最小二乘法
import numpy as np   ##科学计算库
import scipy as sp   ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt  ##绘图库
# python中已经有最小二乘方法的函数，只需要按照规定调用即可
from scipy.optimize import leastsq  ##引入最小二乘法算法，

'''
     设置样本数据，真实数据需要在这里处理
'''
##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([1,2,3,4,5])
Yi=np.array([6,5,7,10,12])
'''
    设定拟合函数和偏差函数
    函数的形状确定过程：
    1.先画样本图像
    2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''

##需要拟合的函数func :指定函数的形状
def func(p,x):
    k,b=p
    return k*x+b

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
    return func(p,x)-y

'''
    主要部分：附带部分说明
    1.leastsq函数的返回值tuple，第一个元素是求解结果，第二个是求解的代价值(个人理解)
    2.官网的原话（第二个值）：Value of the cost function at the solution
    3.实例：Para=>(array([ 0.61349535,  1.79409255]), 3)
    4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''
#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[1,20]

#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))

#读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost："+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(k,2))+"x+"+str(round(b,2)))

'''
   绘图，看拟合效果.
   matplotlib默认不支持中文，label设置中文的话需要另行设置
   如果报错，改成英文就可以
'''

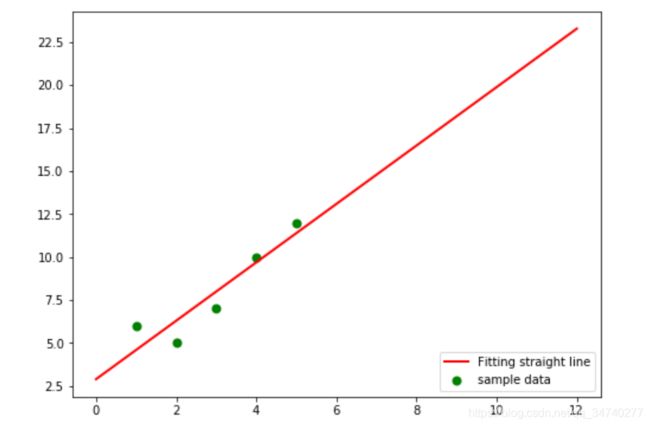
#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="sample data",linewidth=2)

#画拟合直线
x=np.linspace(0,12,100) ##在0-12直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="Fitting straight line",linewidth=2)
plt.legend(loc='lower right') #绘制图例
plt.show()

输出结果