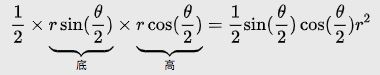数列极限
《目录》
- 极限的概念
- 计算内接多边形的面积
- 柯西数列极限的定义
的极限 = ? ?
- 芝诺悖论
- 魏尔斯特拉斯的数列极限
- 魏尔斯特拉斯数列极限的定义
- 理解复杂式子的方法
- 数列极限的证明
- 数列极限的重要性质及证明
极限的概念
给您一个有意思的视频:《极限是概念》、《无穷小》。
听不懂,也可以看看电影,《无穷小》一定要看!!!
极限:虽不能至,心向往之。
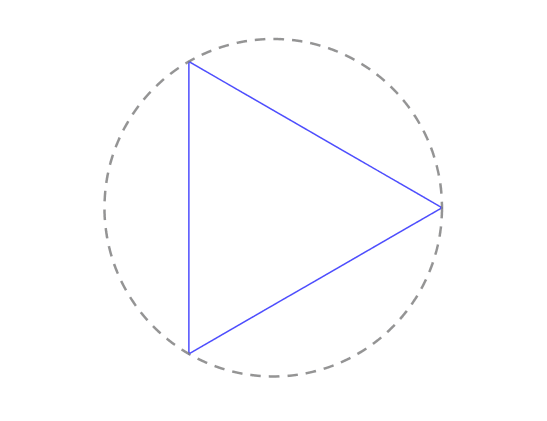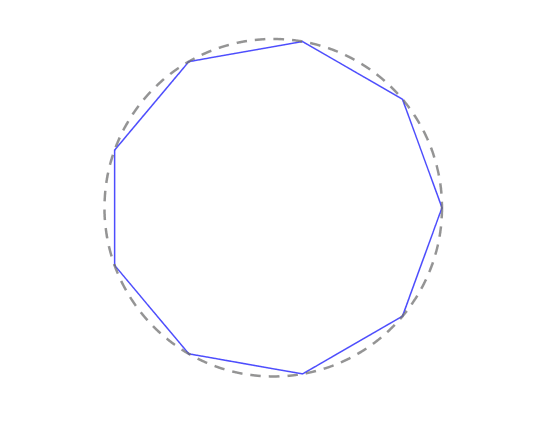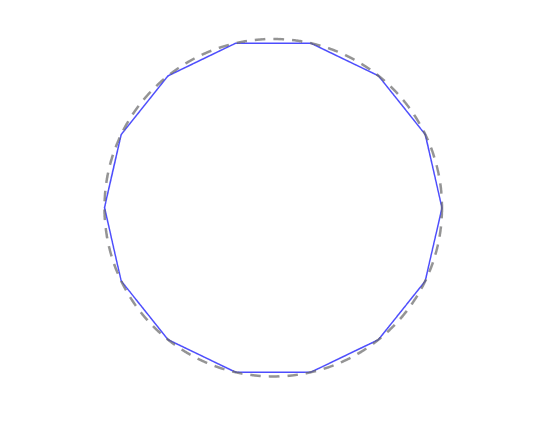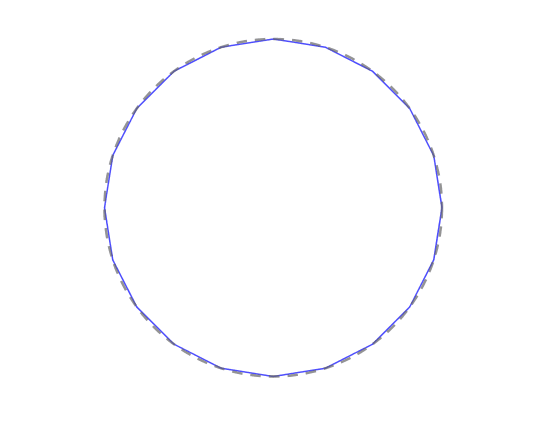
计算内接多边形的面积
内接等边多边形能来逼近圆的面积,可内接等边多边形的面积又怎么算呢 ?
建议从最简单的情况入手,也就是当内接等边多边形是三角形的情况:
![]()
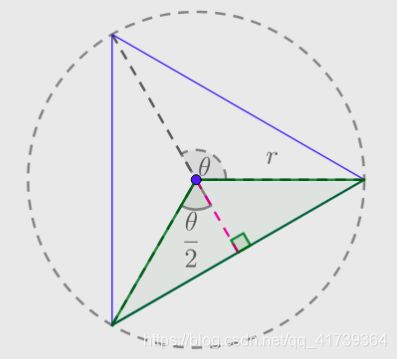
【推导过程】
分析上图,已知 ![]() ,圆的半径为
,圆的半径为 ![]() 。
。
作一个辅助线,通过圆心向某条边做垂线:
上图的绿色三角形被切分成了俩个更小的三角形,三角形的面积公式: ![]() 。
。
内接等边三角形刚好是绿色三角形面积的 ![]() 倍,因此:
倍,因此:![]() 。
。
而 ![]() ,所以:
,所以: ![]()
![]()
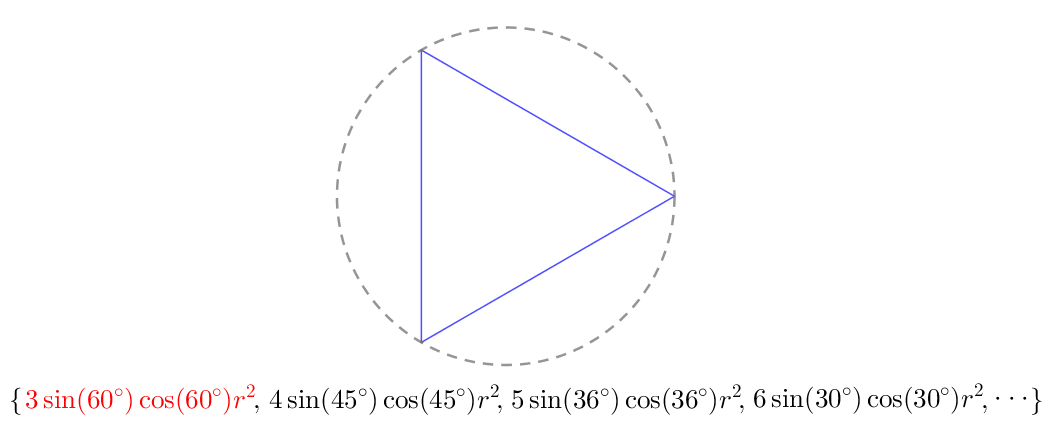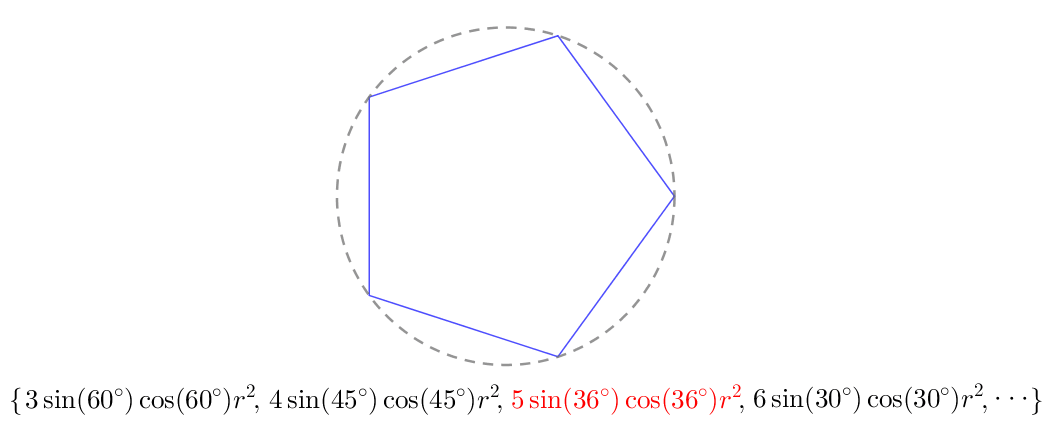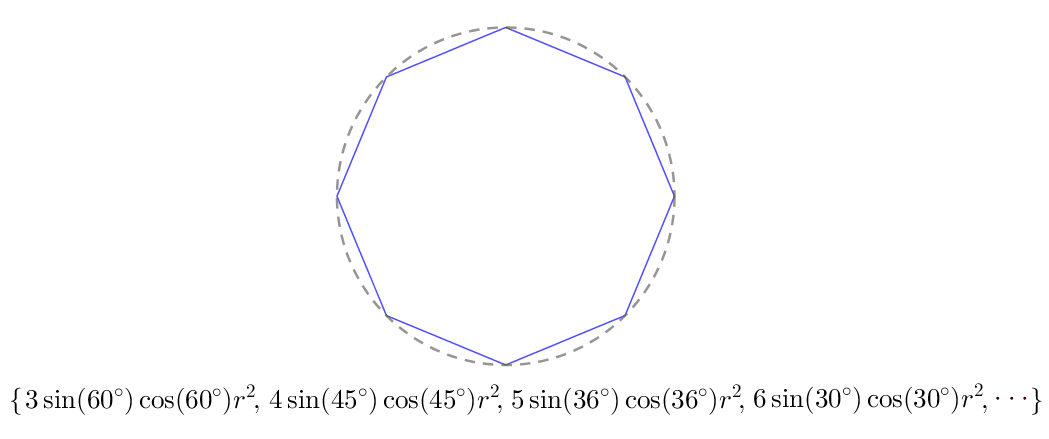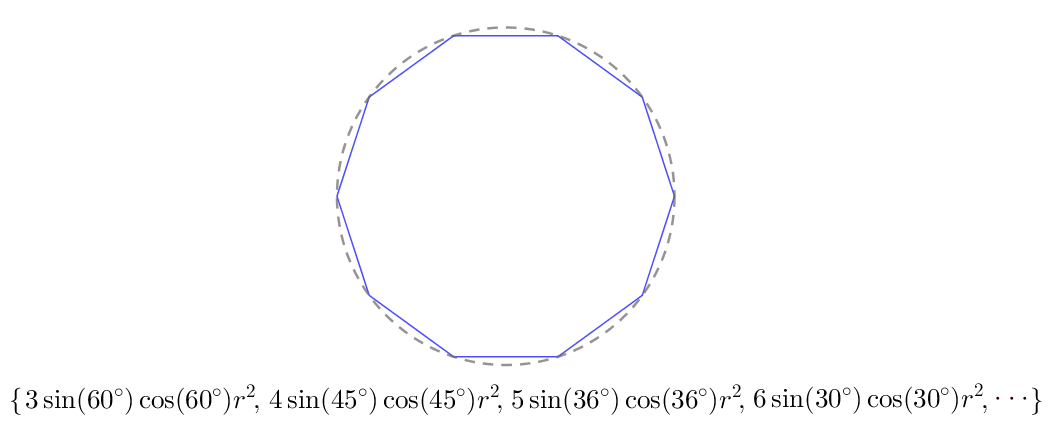
一般化后就能推出:
柯西数列极限的定义
俩个世纪后,数学家柯西使用了极限理论。
柯西把这些等边多边形的面积用花括号扩起来,称之为数列:
![]()
数列的定义:
这个静态的数列实际上表示了逼近这一过程(很神奇):
按照对内接等边 ![]() 边形的面积的分析,数列可以写完变量的形式:
边形的面积的分析,数列可以写完变量的形式:![]() 。
。
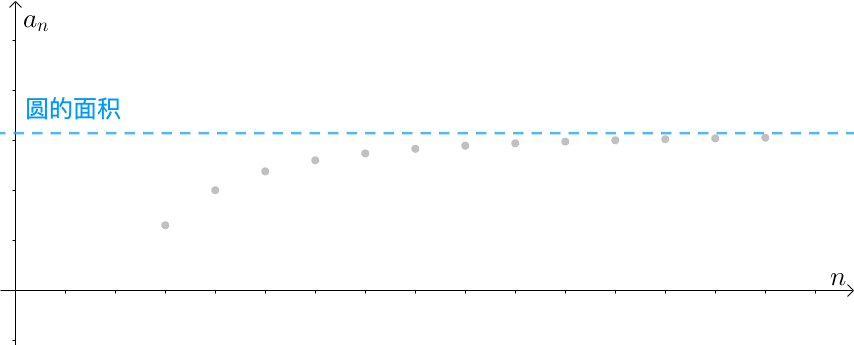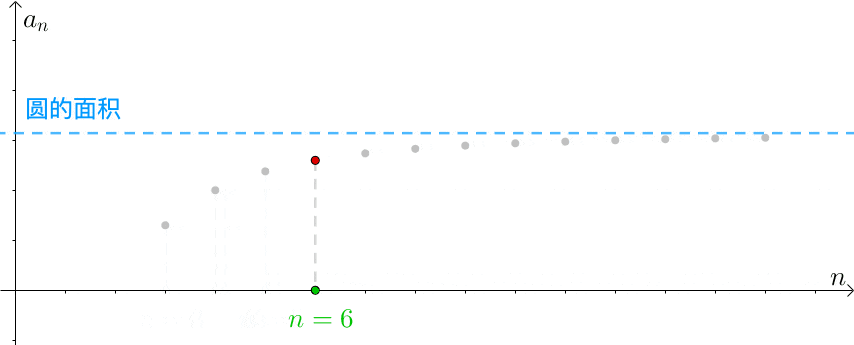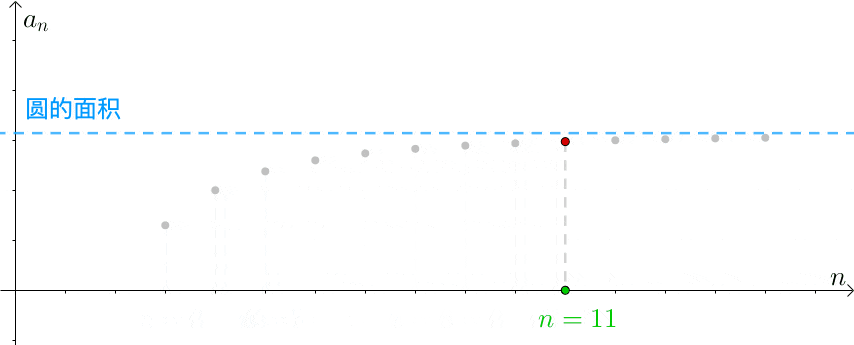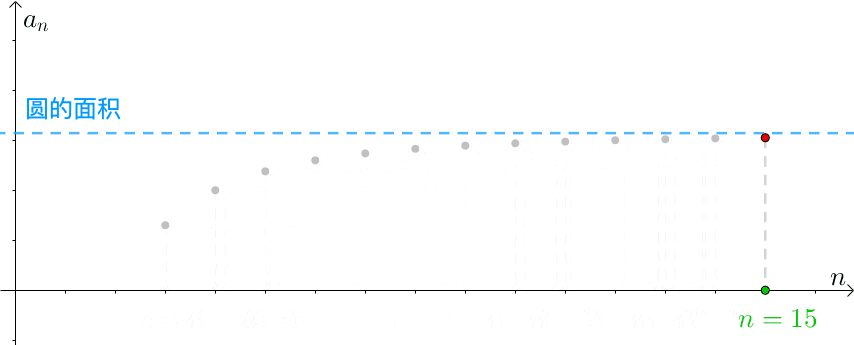
函数图像:随着边数 ![]() 的增加,数列逼近面积的误差越小:
的增加,数列逼近面积的误差越小:
用代数表示:
![]()
柯西成功的把逼近转为了严格的数学对象,数列。并且给出了数列的极限的定义:
柯西数列极限的定义:若某数列无限地趋向于某一实数,与该实数的差可以任意小,则该确定的实数称为此数列的极限。
 的极限 = ? ?
的极限 = ? ?
埃利亚学派古希腊哲学家巴尔尼德强调:"能被思想的就能存在" 存在本身的说法引起了很多人的批评与嘲笑。
芝诺为了替老师辩护,发展出一种特殊的哲学方法 --"归谬法"。
所谓的“归谬法”就是您跟别人在辩论的时候,您先暂时接受别人说的是对的,然后再通过举例、论证来说明,最后证明结论是荒谬的,这叫做“归谬法”。
双方辩论时,您证明自己的说法有时候更不容易,还不如先暂且接受对手是对的,然后再说他那个对的说法最后会得到荒谬的结论。
芝诺:既然我老师说没有变化,所以我就要告诉你们,你们以为有变化,是因为你们认为变化出现,变化代表很多东西存在,从这个变成那个,有多样性;同时变化一定在时间、空间里面展开,所以你们认为有时间、空间还有多元的东西。那我现在告诉你们,你们所认为的三点:有变化、有时间、有空间都是错误的。
为此,芝诺举了四十几个 "悖论",如著名的:
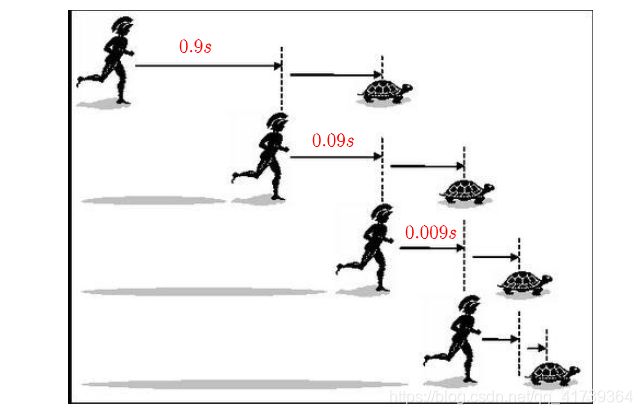
阿喀琉斯(Achilles)是有名的飞毛腿,跑得飞快的,但是他如果让乌龟先走一步,他就永远追不上乌龟了。
而我们学习的是,与之类似的问题......
证明 0.999··· = 1。
1 = 1,这个不用证明了,可以直接用。
- 1 = 1
将等式俩边同时除以 3 ,左边写成小数形式,右边写成分数形式,
- 0.333··· =

俩边同时 *3 ,得
- 0.999··· = 1
证毕,您觉得这样证明对不对呢 ? ? ?
其实有许多证法,这是不标准的证法之一,说不标准是因为证后还是让人不明所以,证明后更加混乱了。
我们可以把 0.999···999,组成一个无穷集合P。
那么 n 越大,就越接近 1,但 无论 n 多大,![]() 一定小于 1。
一定小于 1。
- 0.999···9 < 1
- 0.999··· = 1
想一想,这是为什么 ?
0.9,0.99,0.999,0.999···9, 一直延伸会无限的接近 1 --- 在一个数列中,0.999··· 就是 1 的书写形式。
- 0.999··· 表示 1
即使, 0.9,0.99,0.999,0.999···9一直延伸,1也是出不来的,0.999···表示的就是 这个出不来的 1。
所以,
所以, 0.999··· = 1, 证毕。 (您可以简单的理解为只是一种书写形式的变化,就好像表示某个数值,不一定只能用10进制)
如果使用一般化方法,把具体数 0.9,0.99,0.999,0.999···9 抽象为 ,把 1 抽象为 某个数 记为 ?,
n --> ∞ 时
--> ?
因此 , ![]() 的极限 = ? . ?是数列指向的目标,数列经过 无限操作 后依然不能达到的目标呢!
的极限 = ? . ?是数列指向的目标,数列经过 无限操作 后依然不能达到的目标呢!
得到了全世界,为什么就是得不到你 ! ! ! --- 虽然不能至,❤️ 向往之。
![]()
我们刚刚学习的极限“虽不能至,心向往之”就是解决 芝诺悖论 的必要条件。
芝诺悖论
在南意大利 有俩大学派,一个是毕达哥拉斯学派,另一个就是爱利亚派 ,巴门尼德则是其中的领袖。
巴门尼德说万物起源,不应该只关注质料,如 水、气、火,或是 关注 TA 的形式,如数学,而是应该关注那唯一的 “存在本身”。
如果有一样东西真的存在,TA一定能够被我们谈论,能被我们谈论,一定能被我们思想,因此,能被思想与存在是一起的,TA 就是永恒、唯一的。
巴门尼德的这句话启蒙了唯心论(柏拉图) 和 唯物论(德谟克利特),其中 "存在与思想一致性原则" 是巴门尼德的主要理论。
总的来说,赫拉克利特 认为一切都在变化之中,而巴门尼德认为万物没有任何变化,否定了 "时间"、"空间"、"变化"。
这说话当然引起了很多闲杂人等的批评和嘲笑,巴门尼德的弟子 --- 芝诺 看不过去就说一个著名的论证,也可说为悖论。
大佬出场了。
芝诺:阿喀琉斯(Achilles)是有名的飞毛腿,跑得飞快的,但是他如果让乌龟先走一步,他就永远追不上乌龟了。
无论是哲学家,还是数学家,在没有微积分之前,没有人能解决这个问题(虽然知道这是谬论)。
可我们学了微积分了啊,不妨令阿喀琉斯步行的速度为 ![]() ,乌龟爬行的速度为
,乌龟爬行的速度为 ![]() ,并且在比赛之前,阿喀琉斯让乌龟先爬
,并且在比赛之前,阿喀琉斯让乌龟先爬 ![]() ,在这种条件下,阿喀琉斯追赶乌龟所用的时间是多少呢 ?
,在这种条件下,阿喀琉斯追赶乌龟所用的时间是多少呢 ?
(2). 与此同时,乌龟又爬了, ![]() 。
。
(4). 乌龟又爬了, ![]() 。
。
这些数字按其先后,可以构成一个数列:![]() 。
。
极限:![]() 。
。
所以,阿喀琉斯 ![]() 就能追上乌龟。
就能追上乌龟。
芝诺说的其实就是无限级数求和,只不过他不知道,![]() 并不等于无限大,而是等于
并不等于无限大,而是等于 ![]() !
!
魏尔斯特拉斯的数列极限
柯西定义的数学极限:若某数列无限地趋向于某一实数,与该实数的差要多小就多小,则该确定的实数称为此数列的极限。
这个定义中有几个问题是含混的:
-
什么是“无限”?
-
什么是“无限地趋向于”?
-
什么是“任意小”?
虽然柯西的定义直观易懂,但还不严格呐。
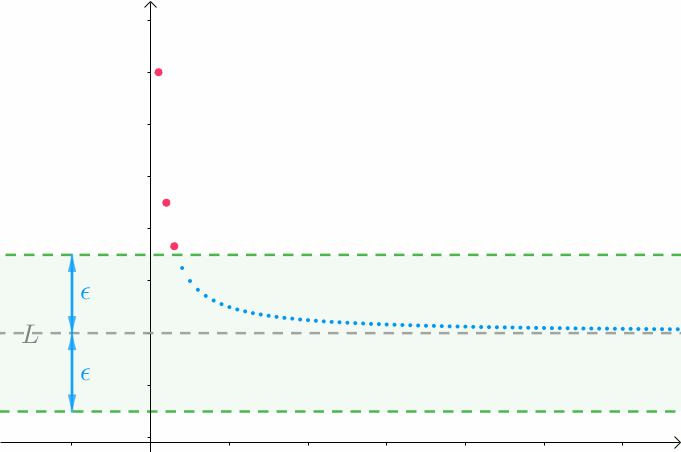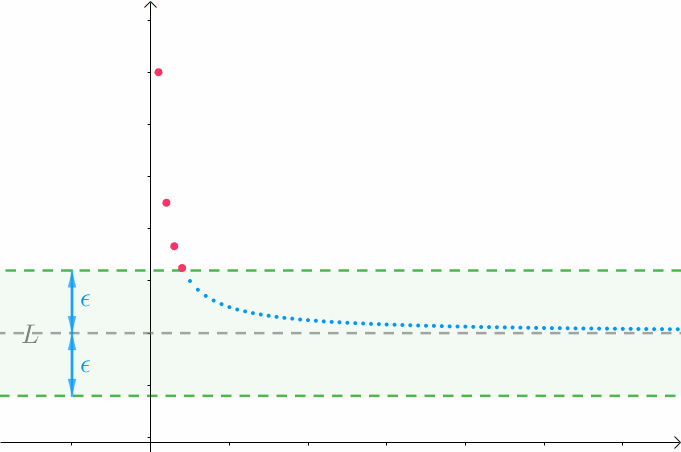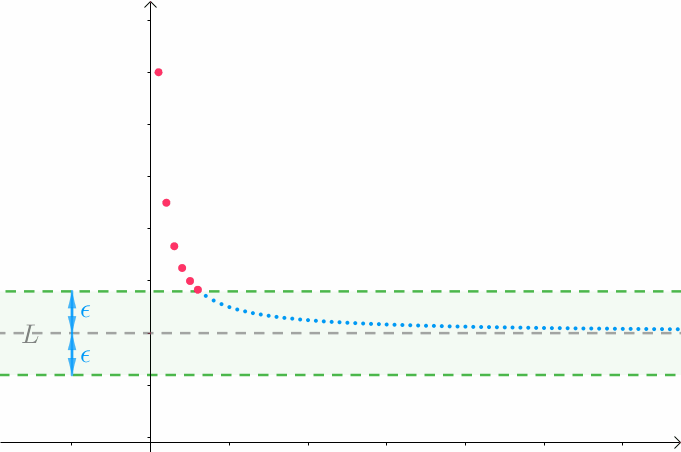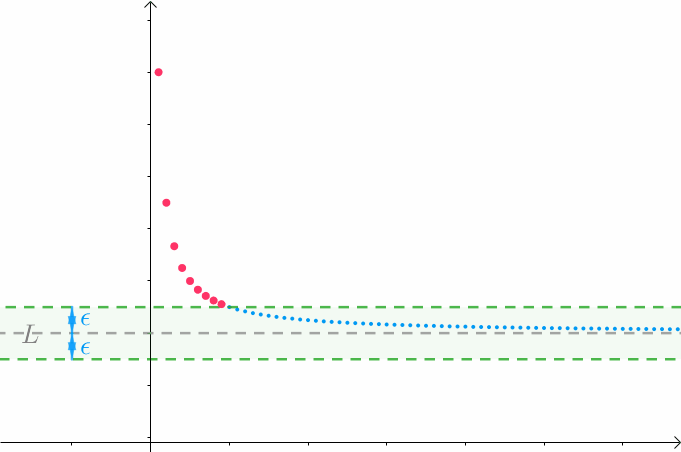
数列图像是趋于 ![]() ,但却是上下浮动。这到底 算不算“无限地趋向于0” ,到底算不算“与0的差可以要多小就多小”?
,但却是上下浮动。这到底 算不算“无限地趋向于0” ,到底算不算“与0的差可以要多小就多小”?
柯西的定义还比较局部,后来维尔斯特拉斯借助不等式,通过俩个变量之间的关系,定量的、具体的刻划了俩个“无限过程”之间的联系解决了柯西数列没有说清楚的定义。(简单来说,柯西用的是人的语言来描述微积分,而维尔斯特拉斯用的是数学语言来描述微积分)
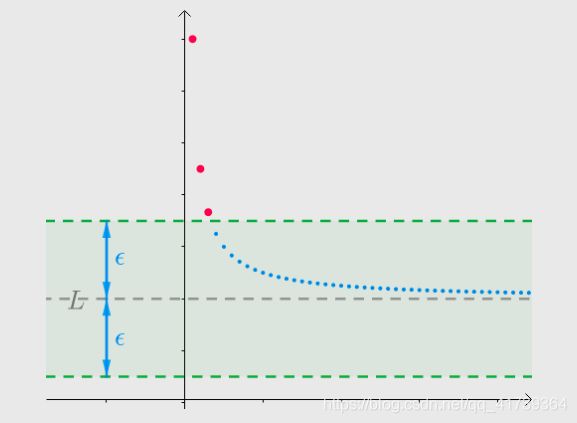
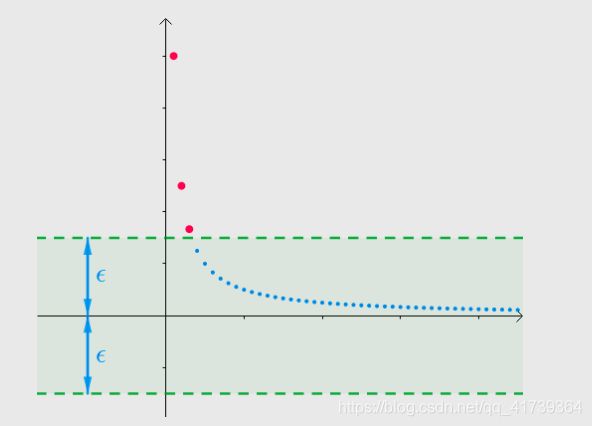
魏尔斯特拉斯大概是这么考虑的,假如有这样一个数列,猜猜某实数 ![]() 为数列的极限,再用一根平行
为数列的极限,再用一根平行 ![]() 轴的虚线表示:
轴的虚线表示:
任意给一个正实数 ![]() ,以
,以 ![]() 为中心做一个区间(绿色区间),此时有有限个点在此区间外(红点):
为中心做一个区间(绿色区间),此时有有限个点在此区间外(红点):
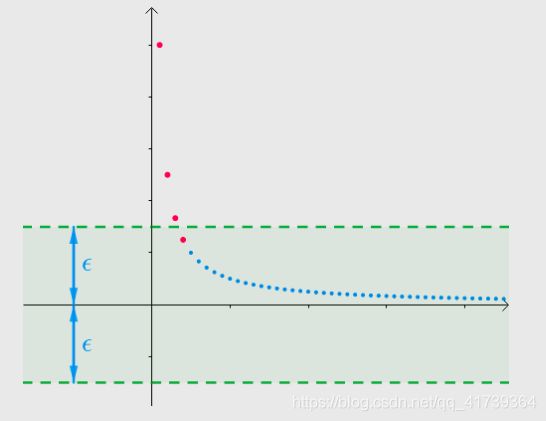
随着正实数 ![]() 的变小(越来越逼近
的变小(越来越逼近 ![]() ),始终只有【有限个点】在此区间外:
),始终只有【有限个点】在此区间外:
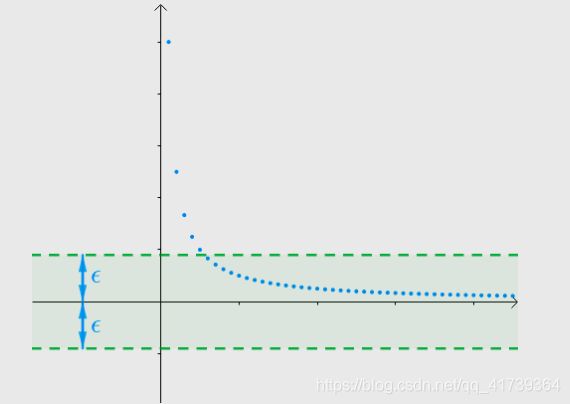
若是没猜对,随着正实数 ![]() 的缩小,会有无数个点在此区间外:
的缩小,会有无数个点在此区间外:
神马都是浮云,这种思路很独特:
- 极限
 是猜测的,具体的猜法待续;
是猜测的,具体的猜法待续; - 正实数
 是任取的,只要能逼近
是任取的,只要能逼近  。
。
魏尔斯特拉斯数列极限的定义
我们看看数学语言(涉及到一些高等数学的符号)是如何描述上面的思路:
![]() 代表任意,
代表任意,![]() 代表存在。
代表存在。
写成一句话就是:![]() 正整数
正整数 ![]() 当
当 ![]() 时,有
时,有 ![]() 。
。
或者是:![]() 。
。
或者是:![]() 。
。
只要理解了这句话,这篇文章基本不用看了,数列的极限都懂了,最多看一下证明。
理解复杂式子的方法
我们试着解读这样一个式子:![]() 。
。
这个式子有点复杂,拆分着读即可。
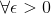
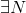
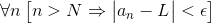
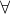 代表任意,
代表任意,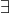 代表存在。
代表存在。
为了明确符号 ![]() 、
、![]() 的有效范围,我们加一些大括号。
的有效范围,我们加一些大括号。
![]()
从左开始:
![\forall \epsilon >0\left [ ~~ \right ]](http://img.e-com-net.com/image/info8/4e5e5b56e5954485a5f17ee4c55903d2.gif) 数学语言转自然语言:对于任意正数
数学语言转自然语言:对于任意正数 。
。![\forall \epsilon >0\left [ ~~\exists N ~~\left [ ~~\right ]\right~ ]](http://img.e-com-net.com/image/info8/a7688c5d26074319892576f6ac1f82bb.gif) 数学语言转自然语言:对于任意正数
数学语言转自然语言:对于任意正数 ,都存在某个自然数
,都存在某个自然数 。
。![\forall \epsilon >0\left [ ~~\exists N ~~\left [ ~~\forall n~~\left [ ~~ \right ]~\right ]\right~ ]](http://img.e-com-net.com/image/info8/8228db8f313c4cd8879beba391a2ff2c.gif) 数学语言转自然语言:对于任意正数
数学语言转自然语言:对于任意正数 ,都存在某个自然数
,都存在某个自然数 ,使得 ..... 对任意自然数
,使得 ..... 对任意自然数  都成立。
都成立。![\forall \epsilon >0\left [~~\exists N ~~\left [ ~~\forall n\begin{bmatrix} n>N\Rightarrow \begin{vmatrix} a_{n}-L \end{vmatrix}<\epsilon \end{bmatrix}~~ \right ]~\right ]\right~](http://img.e-com-net.com/image/info8/b472b324f7354c82bbac64caa4666870.gif) ,填上括号里面的内容。
,填上括号里面的内容。
数学语言转自然语言:对于任意正数![]() ,都存在某个自然数
,都存在某个自然数![]() ,使得 【
,使得 【 ![]() 】对任意自然数
】对任意自然数 ![]() 都成立。
都成立。
我们再润润色:若对于任意正数![]() ,给每个
,给每个![]() 都选定某个合适的自然数
都选定某个合适的自然数![]() ,则能使命题
,则能使命题 ![]() 对于任意自然数
对于任意自然数 ![]() 都成立。
都成立。
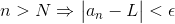 数学语言转自然语言:若
数学语言转自然语言:若  大于
大于  ,则点
,则点  与点
与点  的距离小于
的距离小于  。
。
如果换成“邻域”(类似区间的表示法)就是:若 ![]() 大于
大于 ![]() ,则点
,则点 ![]() 在点的
在点的 ![]() 邻域里。
邻域里。
![\forall \epsilon >0\left [~~\exists N ~~\left [ ~~\forall n\begin{bmatrix} n>N\Rightarrow \begin{vmatrix} a_{n}-L \end{vmatrix}<\epsilon \end{bmatrix}~~ \right ]~\right ]\right~](http://img.e-com-net.com/image/info8/b472b324f7354c82bbac64caa4666870.gif) 总结在一起:若对于任意正数
总结在一起:若对于任意正数 ,给每个
,给每个 都选定某个合适的自然数
都选定某个合适的自然数 ,则能使命题【若
,则能使命题【若  大于
大于  ,则点
,则点  在点
在点  的
的  邻域里】对于任意自然数
邻域里】对于任意自然数  都成立。
都成立。
用人话说:不管是多窄的 ![]() 邻域,只要根据
邻域,只要根据 ![]() 丢掉开头的前 N 项,就能把剩下的所有项一股脑的放进
丢掉开头的前 N 项,就能把剩下的所有项一股脑的放进 ![]() 的邻域里。
的邻域里。
练习
实战一下,大概就明白了。
求
,即
在电脑里画出数列的图像:
![]()
合理猜测数列的极限为 0,也就是假设:
接着验证这个假设是否正确,![]() 的意思是随意选一个
的意思是随意选一个 ![]() ,如
,如 ![]() ,以
,以 ![]() 为中心构建区间:
为中心构建区间:
只有三个点在区间外,再用极限定义计算下,区间内的点需要满足的条件是:
解不等式,可得以下条件满足时,上述不等式成立:
当 ![]() 时,此不等式不成立。
时,此不等式不成立。
所以,进一步假设 ![]() ,此时
,此时 ![]() 时,排除掉前四个点,从第五个点开始就全在区间内了:
时,排除掉前四个点,从第五个点开始就全在区间内了:
可见,多排除了一个点。不过不重要,我们关心的是否有无数点在区间内,多一个、少一个对判断没影响。
换成数学语言就是:![]() 时,
时,![]() 有
有 ![]() 。
。
再进一步减小,![]() 取
取 ![]() 又如何:
又如何:
如果任意选择正数 ![]() ,需要满足:
,需要满足:![]() 。
。
因此,只要选择 ![]() ,就
,就 ![]() 时有:
时有:![]() 。
。
数学语言和编程语言一样,多用就会了,因此:![]() 。
。
数列极限的证明
如何用数列的定义来证明数列的极限 ?
思路是:用
求
,
是可以确定的,通常我们就会假设
是某个值。
这个数列的极限就是 1:![]() 。
。
极限是 1,减去 1:![]() 。
。
要在这个等式成立的情况下,找出 N 证明就完成了。
如果数列的极限不是真的,是找不到 ![]() 的。
的。
数列极限的重要性质及证明
数列极限的重要性质及证明主要有 4 个:
- 极限唯一性:只有一个极限
- 有界
- 保号
- 子数列收敛于同数列
采用反证法,证明数列极限唯一性
假设数列有俩个不相等的极限 a、b,a < b。
根据极限定义:
,当
,当
,当
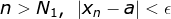
,当
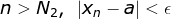
,当
,展开第一个式子:
接着算第二个极限是 b 的,算出
,和第一个极限是 a 的矛盾了。
所以说,数列如果收敛的,那TA的极限是唯一的。
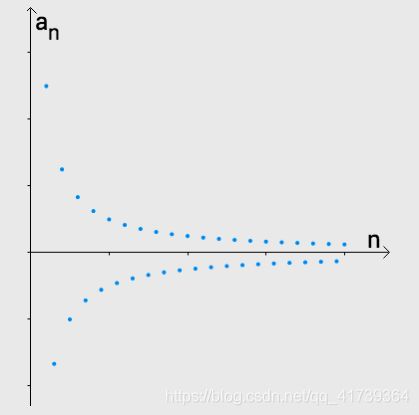
反例:证明
是发散的。