杭电3635————并查集的应用（路径压缩）

Dragon Balls

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3182    Accepted Submission(s): 1227

Problem Description

Five hundred years later, the number of dragon balls will increase unexpectedly, so it's too difficult for Monkey King(WuKong) to gather all of the dragon balls together. 

His country has N cities and there are exactly N dragon balls in the world. At first, for the ith dragon ball, the sacred dragon will puts it in the ith city. Through long years, some cities' dragon ball(s) would be transported to other cities. To save physical strength WuKong plans to take Flying Nimbus Cloud, a magical flying cloud to gather dragon balls. 
Every time WuKong will collect the information of one dragon ball, he will ask you the information of that ball. You must tell him which city the ball is located and how many dragon balls are there in that city, you also need to tell him how many times the ball has been transported so far.

 

Input

The first line of the input is a single positive integer T(0 < T <= 100). 
For each case, the first line contains two integers: N and Q (2 < N <= 10000 , 2 < Q <= 10000).
Each of the following Q lines contains either a fact or a question as the follow format:
  T A B : All the dragon balls which are in the same city with A have been transported to the city the Bth ball in. You can assume that the two cities are different.
  Q A : WuKong want to know X (the id of the city Ath ball is in), Y (the count of balls in Xth city) and Z (the tranporting times of the Ath ball). (1 <= A, B <= N)

 

Output

For each test case, output the test case number formated as sample output. Then for each query, output a line with three integers X Y Z saparated by a blank space.

 

Sample Input

2 3 3 T 1 2 T 3 2 Q 2 3 4 T 1 2 Q 1 T 1 3 Q 1

 

Sample Output

Case 1: 2 3 0 Case 2: 2 2 1 3 3 2

刚看到的时候不知道怎么做，后来发现时归类到并查集的题于是慢慢有了一点思路。

设定了三个数组。

1.ball[i] 表示龙珠i在哪个城市 初始化为ball[i] = i

2.city[i] 表示城市i一共有多少龙珠 初始化为city[i] = 1 因为开始的时候ith龙珠在ith城市

3.transport[i] 表示龙珠i移动了多少次 初始化为0

思想是这样的，就是读取 T x y 的语句时，Union(x,y) 建立x和y城市的联系，不断这样，最后生成的树就是龙珠在各个城市间的转移树。

在转移树中，i的根节点就是最后i龙珠所在的城市号。(如果不能理解的话试着画一画模拟一下并查集的Union——find过程就会清楚)

然后输出有三个：

1.龙珠i在哪个城市 解决：find_root(i)函数就可以找到i龙珠最后在哪个城市

2.城市find_root(i)中有多少个龙珠 解决：直接输出city[find_root(i)]即可

3.龙珠i转移了多少次 解决：？？

3就是最愁人的.....

一个非常合理的想法是：

当读取 T x y时，就是要把x中的所有龙珠转移到y城市当中，那么x城市当中的龙珠的transport都要+1，这就要求我们每次转移时都要搜索哪些龙珠在x城市中，虽然这个算法不难但是太耗时间了（据说会超时我没有尝试不过无疑这不是很“聪明”的策略）

于是学到了一个新的名词————路径压缩。

关于路径压缩，维基百科解释如下：

第二个优化，称为“路径压缩”，是一种在执行“查找”时扁平化树结构的方法。关键在于在路径上的每个节点都可以直接连接到根上；他们都有同样的表示方法。为了达到这样的效果，Find递归地经过树，改变每一个节点的引用到根节点。得到的树将更加扁平，为以后直接或者间接引用节点的操作加速

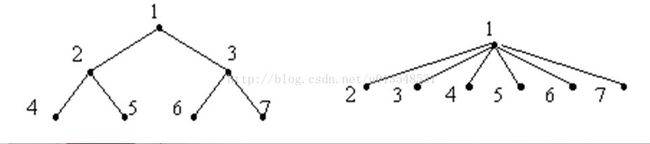
到底什么是扁平化呢？？其实就是下图的意思：

这样应该很明了了，极大的缩小了树的秩（深度），那么在寻找根节点时会很方便。

给出一段代码：

int getfather(int v)
{
    if (father[v]==v)
      return v;
    else
    {
        father[v]=getfather(father[v]);//路径压缩
        return father[v];
     }
}

或者简短的写

int getfather(int v)
{
	return (v == father[v]) ? v : getfather(father[v]);
}

上面这一段是递归实现的，给出非递归实现（防止栈溢出）

int find_root(int x)
{
	int root;    
	root = x;    
	while( root != father[root])            
		root = father[root];        
	return root;         
}

以上就是对路径压缩的一点浅显的介绍。

下面再回到题目上来：

对于问题3，龙珠转移了多少次，可以用这样的思想：

将要转移的龙珠所在城市的根结点的转移次数+1，等到以后路径压缩时，子结点自己移动的次数加上根结点移动的次数，就是这个结点总共的移动次数。可能有点绕，稍微从文字角度上说一下。

比如说要把城市i的龙珠转移到j，先让i所在树的根（这里的根其实就是i城市本来有的龙珠也就是i号龙珠）的转移次数为1（因为第一次转移）

然后从开始向根节点路径压缩。假设从i到顶点一共有四层（也就是说，目前i城市里边有4颗龙珠，根节点龙珠是i号）

根结点为1号龙珠（根节点），然后第二层2号龙珠，第三层3号龙珠，第四层4号龙珠.那么，第一层路径压缩过程中进入第二层，然后第三层，然后第四层，第四层也就是根，找到根结点，返回第三层，第三层+上第四层的转移次数，然后返回第二层，第二层转移次数加上第三层转移次数，返回第一层，第一层转移次数加上第二层转移次数，同时，在这个过程中也把下面3层的结点的父节点直接更新为和根结点，也就是1相连。

下附代码（687MS....很慢了我不知道怎么优化了）

#include 
#include 
#define maxn 10005

int transport[maxn];//transport[i]表示i球转移了多少次
int ball[maxn];//ball[i]表示i球在哪个城市,其实是并查集中的集合 
int city[maxn];//city[i]表示i号城市有几个球 
/*带权并查集*/
void initialize()
{
	for(int i = 0 ; i <= maxn - 1 ; ++i)
	{
		ball[i] = i;//初始i号球在i城市 
		city[i] = 1;//初始i城市只有一个球 
		transport[i] = 0;//初始i号球没有经过任何转移 
	}
}
int find_root(int x)
{	
    //ball[x]是x的父节点 
	if(x == ball[x])
		return x;
	int temp = ball[x]; 
	ball[x] = find_root(ball[x]);
	transport[x] += transport[temp];
	//注意这条语句和上条顺序不可颠倒，这一过程是在回溯时完成的 
	return ball[x];	
}
void Union(int x,int y)
{
	int root1 = find_root(x);
	int root2 = find_root(y);
	if(root1 != root2)
	{
		ball[root1] = root2;
		transport[root1] = 1;//第一次移动 
		city[root2] += city[root1]; 
		city[root1] = 0;//移动完毕后置0 
		//这里的city其实是并查集的树的高度。 
	}
}
int main()
{
	int Case;
	int balls,query;
	int from,to;
	char cmd[5];
	
	scanf("%d",&Case);
	int count = 0;
	while(Case--)
	{
		initialize();
		printf("Case %d:\n",++count);
		scanf("%d%d",&balls,&query);
		while(query--)
		{
			scanf("%s",cmd);
			if(cmd[0] == 'Q')
			{
				int k;
				scanf("%d",&k);
				int x = find_root(k);
				printf("%d %d %d\n",x,city[x],transport[k]);
			}
			if(cmd[0] == 'T')
			{
				scanf("%d%d",&from,&to);
				Union(from,to);
			}
		}
	}
	return 0;
}

转载于:https://www.cnblogs.com/sixdaycoder/p/4348377.html