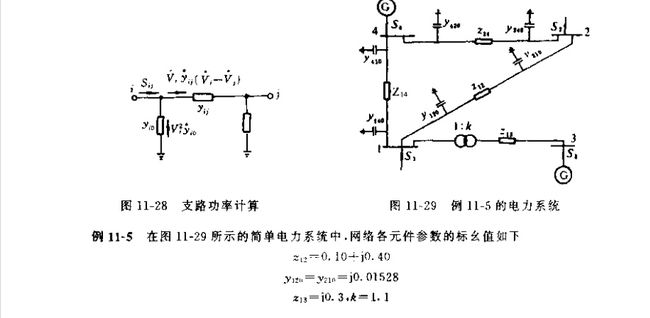
题目描述:
在图所示的电力系统中,网络各元件参数的标幺值如下.......试用牛顿法计算潮流分布。
程序代码
clc %清空command windows
clear all %清空workspace
N=4;
NPQ=2;
NPV=1;
K=1;
Kmax=1000 ;
s=10^(-5);
G=[1.042093 -0.588235 0 -0.453858;
-0.588235 1.069005 0 -0.480769;
0 0 0 0 ;
-0.453858 -0.480769 0 0.934627 ];
B=[ -8.242876 2.352941 3.666667 1.891074 ;
2.352941 -4.727377 0 2.403846 ;
3.666667 0 -3.3333333 0 ;
1.891074 2.403846 0 -4.261590 ];
Y=complex(G,B);
Pnode=[ -0.3 -0.55 0.5 ];
Qnode=[ -0.18 -0.13 0 ];
Vnode=[ 0 0 1.10 ];
e=[ 1.0 1.0 1.1 1.05 ];
f=[ 0 0 0 0 ];
%利用for循环来实现多次迭代。
for K=1:Kmax,
%计算△W。
for i=1:2, %PQ
dP(i)=Pnode(i);
dQ(i)=Qnode(i);
end
%不断地累减,得△P和△Q
for i=1:2,
for j=1:N,
dP(i)=dP(i)-e(i)*G(i,j)*e(j)+e(i)*B(i,j)*f(j)-f(i)*G(i,j)*f(j)-f(i)*B(i,j)*e(j);%△P
dQ(i)=dQ(i)-f(i)*G(i,j)*e(j)+f(i)*B(i,j)*f(j)+e(i)*G(i,j)*f(j)+e(i)*B(i,j)*e(j);%△Q
end
end
%计算NPV个PV节点的△P、(△V)^2 先初始化,再不断地累减
%初始化
for i=(NPQ+1):(N-1),
dP(i)=Pnode(i);
end
%不断地累减,得△P和(△V)^2 =dV2(i)
for i=(NPQ+1):(N-1),
for j=1:N,
dP(i)=dP(i)-e(i)*G(i,j)*e(j)+e(i)*B(i,j)*f(j)-f(i)*G(i,j)*f(j)-f(i)*B(i,j)*e(j);
dV2(i)=Vnode(i)^2-e(i)^2-f(i)^2;
end
end
a=1;
for i=1:(N-1),
dW(a)=dP(i);
a=a+2;
end
%将△Q间隔地赋入△W
a=2;
for i=1:NPQ,
dW(a)=dQ(i);
a=a+2;
end
%将△V^2间隔地赋入△W
a=NPQ*2+2;
for i=(NPQ+1):(NPQ+NPV),
dW(a)=dV2(i);
a=a+2;
end
%判断是否小于ε
if max(dW)
fprintf('\n 迭代是收敛的。第%d次迭代后终止迭代。\n',K-1);
break;
end
%计算雅克比矩阵各元素。 算法:先初始化,再不断地累减
J=zeros(N-1);
%初始化
for i=1:N-1,
for j=1:N-1,
if i<=NPQ %求雅克比矩阵中PQ节点的元素
if i==j
J(2*i-1,2*j-1) = -G(i,i)*e(i)-B(i,i)*f(i);
J(2*i-1,2*j ) = B(i,i)*e(i)-G(i,i)*f(i);
J(2*i ,2*j-1) = B(i,i)*e(i)-G(i,i)*f(i);
J(2*i ,2*j ) = G(i,i)*e(i)+B(i,i)*f(i);
for k=1:N,
J(2*i-1,2*i-1) = J(2*i-1,2*i-1)-G(i,k)*e(k)+B(i,k)*f(k);
J(2*i-1,2*i ) = J(2*i-1,2*i )-G(i,k)*f(k)-B(i,k)*e(k);
J(2*i ,2*i-1) = J(2*i ,2*i-1)+G(i,k)*f(k)+B(i,k)*e(k);
J(2*i ,2*i ) = J(2*i ,2*i )-G(i,k)*e(k)+B(i,k)*f(k);
end
elseif i~=j
J(2*i-1,2*j-1) = -G(i,j)*e(i)-B(i,j)*f(i);
J(2*i-1,2*j ) = B(i,j)*e(i)-G(i,j)*f(i);
J(2*i ,2*j-1) = B(i,j)*e(i)-G(i,j)*f(i);
J(2*i ,2*j ) = G(i,j)*e(i)+B(i,j)*f(i);
end
end
if i>NPQ %求雅克比矩阵中PV节点的元素
if i==j
J(2*i-1,2*j-1) = -G(i,i)*e(i)-B(i,i)*f(i);
J(2*i-1,2*j ) = B(i,i)*e(i)-G(i,i)*f(i);
J(2*i ,2*j-1) = -2*e(i);
J(2*i ,2*j ) = -2*f(i);
for k=1:N,
J(2*i-1,2*i-1) = J(2*i-1,2*i-1)-G(i,k)*e(k)+B(i,k)*f(k);
J(2*i-1,2*i ) = J(2*i-1,2*i )-G(i,k)*f(k)-B(i,k)*e(k);
end
elseif i~=j
J(2*i-1,2*j-1) = -G(i,j)*e(i)-B(i,j)*f(i);
J(2*i-1,2*j ) = B(i,j)*e(i)-G(i,j)*f(i);
J(2*i ,2*j-1) = 0;
J(2*i ,2*j ) = 0;
end
end
end
end
%根据△W=-J*△V, 得△V
dV=(-J)\dW';
%用dV对e、f进行修正,并得到复数表示的V
for i=1:(N-1),
e(i)=e(i)+dV(2*i-1);
f(i)=f(i)+dV(2*i );
V(i)=complex(e(i),f(i));
end
V(N)=complex(e(N),f(N));
format long g;
fprintf('\n 第%d次迭代',K);
V
dW
end
运行结果
第1次迭代
V =Columns 1 through 2
0.993514216814943 - 0.00882844639325065i 0.976339009868481 - 0.107817878429079i
Columns 3 through 4
1.1 + 0.126652332934368i 1.05 + 0i
dW =Columns 1 through 4
-0.2773071 -0.050973600000001 -0.52596255 0.0196023000000007
Columns 5 through 6
0.5 0
第2次迭代
V =Columns 1 through 2
0.984747556450846 - 0.00858486289103918i 0.959002712892889 - 0.108374041635935i
Columns 3 through 4
1.09244606907871 + 0.128933517085255i 1.05 + 0i
dW =Columns 1 through 4
-0.00133294595315923 -0.00277676438602947 -0.0135290080657811 -0.0547116718789575
Columns 5 through 6
0.00301194536855753 -0.0160408134377179
第3次迭代
V =Columns 1 through 2
0.984636349501068 - 0.00859560046446182i 0.958689612744677 - 0.108386929719187i
Columns 3 through 4
1.09241505000661 + 0.128954875586076i 1.05 + 0i
dW =Columns 1 through 4
-3.6002420694934e-05 -3.72031420685648e-05 -0.000253704312255243 -0.00105962549947103
Columns 5 through 6
6.65806363943644e-05 -6.22656734940892e-05