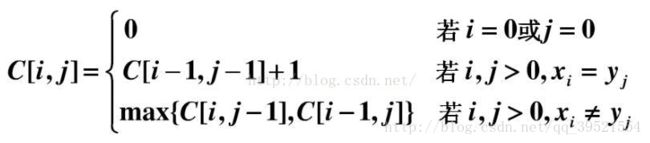动态规划C语言实现之最长公共子序列(LCS)

我的机器学习教程「美团」算法工程师带你入门机器学习   已经开始更新了，欢迎大家订阅~

任何关于算法、编程、AI行业知识或博客内容的问题，可以随时扫码关注公众号「图灵的猫」，加入”学习小组“，沙雕博主在线答疑~此外，公众号内还有更多AI、算法、编程和大数据知识分享，以及免费的SSR节点和学习资料。其他平台（知乎/B站）也是同名「图灵的猫」，不要迷路哦~

 

 

 

 

 

动态规划中，我曾对于01背包和硬币问题有过一些理解，今天参考了博客上其他同学的经验，完成了最长公共子序列LCS的代码实现。具体的算法内容请移步我的另一篇博文：动态规划入门之：最长公共字符串LCS

代码使用C实现，本质上依赖于算法的两个核心：
1.状态转移方程

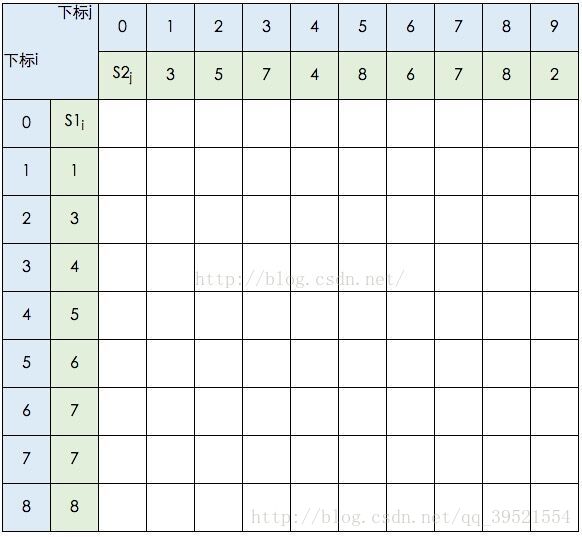
2.状态转移表（数组用来存放位置和长度）

上面都是摘自《算法导论》，如果熟悉这两个内容，那么实现起来就方便许多。代码如下：

 

/***最长公共子序列***/
/*动态规划*/

#include
#include
#include
#include

#ifndef size_c
#define size_c 200
#endif // 预定义字符串的长度

#define EQUAL   1   //EQUAL表示c[i][j]是由c[i-1][j-1]+1来的=此时两个序列有相同的字符
#define UP      2   //UP表示c[i][j]是由c[i-1][j]来的========此时两个序列没有相同的字符
#define LEFT    3   //LEFT表示c[i][j]是由[ci][j-1]来的======此时两个序列没有相同的字符

//int char1[size_c][size_c];  //定义两个二维数组存放字符串
//int char2[size_c][size_c];  //1存放位置，2存放路径

int max(int m, int n, int i, int j);
int print(int i, int j);

/***函数一、判断LCS长度***/
int Lcs_len(char *str1, char *str2, int **char1, int **char2)
{
    //int char1[size_c][size_c] = {0};
    //int char2[size_c][size_c] = {0};

    int m = strlen(str1);
    int n = strlen(str2);  //求出两个数组的边界长度

    int i, j;
    for (i = 0; i <=  m; i++)
    {
        char1[i][0] = 0;
    }

    for (j = 0; j <=  n; j++)  //初始化边界条件
    {
        char1[0][j] = 0;
    }

    for ( i = 1; i <= m; i++)
    {
        for ( j = 1; j <= n; j++)
        {
            if( str1[i-1] == str2[j-1] )
    // 这里使用i-1以及j-1是由于数组的下标从0开始
    //另一种实现方式是逆序实现，对于路径的确定更方便
            {
                char1[i][j] = char1[i-1][j-1] + 1;
                char2[i][j] = EQUAL;
            }
            else if (char1[i-1][j] >= char1[i][j-1])//在j循环时若字符串不等
                {                                // 则只用判断char中的元素
                char1[i][j] = char1[i-1][j];
                char2[i][j] = UP;
                }
            else
                {
                char1[i][j] = char1[i][j-1];
                char2[i][j] = LEFT;
                }
        }


    }
    return char1[m][n];  //递归的最终位存储的数字就是LCS长度
}

/***函数二、输出LCS***/

void Print_Lcs( char *str, int **b, int i, int j)
{
    if( i == 0 || j == 0)
        return;    //递归至边界则扫描完毕
    if( b[i][j] == EQUAL)
    {                     //对于相等的元素，其路径为左上方对角移动
        Print_Lcs(str, b, i - 1, j - 1);
        printf("%c ", str[i-1]);  //相等的话，原字符序列向前递归一位并打印出字符
    }
    else if ( b[i][j] == UP )  //不相等时判断方向：向上则数组向上位移
        Print_Lcs(str, b, i - 1, j);
    else
        Print_Lcs(str, b, i , j - 1); //否则数组下标向左位移一位

}

/***函数三、整合LCS函数***/
void Find_Lcs( char *str1, char *str2)
{
    int i,j,length;
    int len1 = strlen(str1),
        len2 = strlen(str2);
    //申请二维数组
    int **c = (int **)malloc(sizeof(int*) * (len1 + 1));
    int **b = (int **)malloc(sizeof(int*) * (len1 + 1));
    for( i = 0; i<= len1; i++ )  这个等号之前没加，导致内存泄漏
    {
        c[i] = (int *)malloc(sizeof(int) * (len2 + 1));
        b[i] = (int *)malloc(sizeof(int) * (len2 + 1));
    }

    //将c[len1][len2]和b[len1][len2]初始化为0
    for ( i = 0; i<= len1; i++)
        for( j = 0; j <= len2; j++)
        {
            c[i][j] = 0;
            b[i][j] = 0;
        }

    //计算LCS的长度
    length = Lcs_len(str1, str2, c, b);
    printf("The number of the Longest-Common-Subsequence is %d\n", length);

    //利用数组b输出最长子序列
    printf("The Longest-Common-Subsequence is: ");
    Print_Lcs(str1, b, len1, len2);
    printf("\n");

    //动态内存释放
    for ( i = 0; i <= len1; i++)
    {
        free(c[i]);
        free(b[i]);
    }
    free(c);
    free(b);
}

/***LCS测试输出***/

int main(int *argc, int *argv[])
{

    char X[size_c],Y[size_c];
    int len;
    printf("please enter your characters:");
    scanf("%s",X);
    while(strlen(X) > 200) //规定字符串序列的最大长度，此处为200
    {
        printf("what you input is too long, please try again");
        scanf("%s\n",X);//超出限制时提醒并重新输入
    }
    printf("please enter your characters:");
    scanf("%s",Y);
    while(strlen(Y) > 200)  //长度限制同上
    {
        printf("what you input is too long, please try again");
        scanf("%s",Y);
    }

    Find_Lcs(X,Y);  //使用LCS函数输出长度与子序列
    system("pause");
}

 

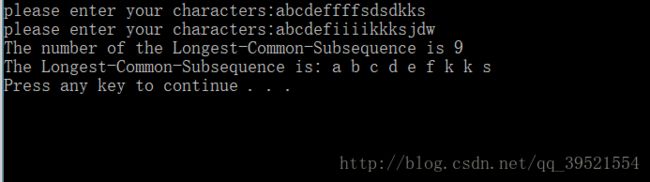
测试结果：