JZ DAY5总结

$昨天休息，搁了一天。$

$DAY5$

$T1$

$超级变变变$

经过一系列的游戏之后，你终于迎来了今天的作业，第一个作业是预习一个超级美好的函数$f(x)$,描述如下。

为了研究这个函数的性质，你决定定义一次变化为$x=f(x)$。若x就经过若干次变化为k，则你就会觉得这是一个k变变数。现在既然你已经这么觉得了，那就只好给定A,B,求有多少个$A<=x<=B$是k变变数了。
输入包含三行。
Input
第一行为一个整数k。
第二行为一个整数A。
第三行为一个整数B。
Output
输出仅一行，表示答案。
Sample Input 1
13
12345
67890123
Sample Output1
8387584
Sample Input2
1
234567
1234567
Sample Output2
1000001
Data Constraint
对于50%的数据，$0<=k,A,B<=10^6$
对于100%的数据，$0<=k,A,B<=10^{18}A<=B$

看完三道题后，马上先回来敲了第一题。前几天考场A过数论题，然我信心大增。怎么说这道题五十$pts$，是暴力随便拿。于是乎就先随手敲了一个暴力，然后开始找规律。
乍一看打出来的表仿佛没什么规律，于是乎便开始手推。其实很明显。
当$k$为偶数时，满足$k$变变数的序列为
$k,k+1,2k,2k+1,2k+2,2k+3,4k,4k+1,4k+2,4k+3\dots \dots +4k+7\dots \dots$
当$k$为奇数时，满足$k$变变数的序列为
$k,2k,2k+1,4k,4k+1,4k+2,4k+3+\dots \dots$
上述两个结论应该都很好想吧，那么且合法的区间为一段连续区间，然后长度以$2$倍增长，因此此题的时间复杂度是$log$级别的，可行。
AC Code:

#include 
#define ll long long
using namespace std;

ll k,a,b,answer,q1,q2;
bool pd;

ll ou(ll p)
{
   ll ans = 0,x,y,jl = 0x3f3f3f3f3f3f3f3f;;
   for (ll i = 1; i * k <= p; i *= 2)
   {
   	if (p <= (i * k + 2 * i - 1)) {x = i; y = p - k * i; pd = 1; break;}
   	if (p - (i * k + 2 * i - 1) < jl) jl = p - (i * k + 2 * i - 1),x = i,y = 2 * i - 1;
   }
   for (ll i = 1; i < x; i *= 2)
   	ans += i * 2;
   ans += y + 1;
   return ans;
}

ll ji(ll p)
{
   ll ans = 0,x,y,jl = 0x3f3f3f3f3f3f3f3f;
   for (int ll i = 1; i * k <= p; i *= 2)
   {
   	if (p <= (i * k + i - 1)) {x = i; y = p - k * i; pd = 1; break;}
   	if (p - (i * k + i - 1) < jl) jl = p - (i * k + i - 1),x = i,y = i - 1;
   }
   for (ll i = 1; i < x; i *= 2)
   	ans += i;
   ans += y + 1;
   return ans;
   
}

int main()
{
   scanf("%lld%lld%lld",&k,&a,&b);
   if (k == 0)
   {
   	printf("%lld",b - a + 1);
   	return 0;
   }
   if (k == 1) 
   {
   	if (a < 1) printf("%lld",b - a); else printf("%lld",b - a + 1);	
   	return 0;
   }
   if (k == 2)
   {
   	if (a <= 1) printf("%lld",b - 1); else printf("%lld",b - a + 1);
   	return 0;
   }
   if (k & 1)
   { 
   	if (b >= k) q1 = ji(b); else q1 = 0;
   	pd = 0;
   	if (a >= k) q2 = ji(a); else q2 = 0;
   	answer = q1 - q2;
   	if (pd) answer ++;
   	printf("%lld",answer);
   } else 
   {
   	if (b >= k) q1 = ou(b); else q1 = 0;
   	pd = 0;
   	if (a >= k) q2 = ou(a); else q2 = 0;
   	answer = q1 - q2;
   	if (pd) answer ++;
   	printf("%lld",answer);
   }
   return 0;
}

有个共性，考场打的代码普遍比较丑，其实有很多可优化的地方，人懒。

$T2$

$图的计数$

在观察完第一个作业之后你终于开始观察第二个作业了，第二个作业十分无聊，就只是一道题目。询问有多少个N个点，M条边的有向图，从1号点到达N号点需要经过至少N-1条边。该有向图中可以包含重边和自环。
Input
第一行两个整数N,M。
Output
仅一个整数表示答案 $mod(10^9+7)$。
Sample Input
2 2
Sample Output
4
Data Constraint
对于30%的数据 N<=5,M<=10
对于60%的数据 N<=80,M<=3000
对于100%的数据 1<=N<=10000 1<=M<=100000
第二题昨晚很晚才搞的一知半解，今天补上。其实上这题通过一个巧妙的转换就变成了一个插板问题。为什么呢，理由如下。
对于这道题，首先构建一条链，即一条从$1$到$N$的链，那么便保证了从1号点到N号点需要经过N - 1条边。对于剩下的$M-(N-1)$条边只要不是捷径其他方法可以随便连。总共的连法$N^2$种，其中捷径有$(N-1)\ast (N-2)/2$种，所以可以的连法只有$N^2-(N-1)\ast (N-2)/2$种，即把$(M-(N-1))$个球，放在$N^2-(N-1)\ast (N-2)/2$个箱子里。那么一共答案便是$C_{N^2-(N-1)\ast (N-2)/2+M-(N-1)-1}^{M-(N-1)}$。此处是一个插板问题的板子，因为由题意可知可以空着不妨所以，可以理解成现在每个盒子里都放上一个球那么就变成了将$N^2-(N-1)\ast (N-2)/2+M-(N-1)-1$个球放在$N^2-(N-1)\ast (N-2)/2+M-(N-1)-1$个盒子的问题。因为直接暴力求会超时，加上一个很显然的小优化即可。
AC Code

#include 
#include 
#define ll long long
using namespace std;

const int mo = 1e9 + 7;
int n,m;
ll ans,x;

ll ksm(ll a,int b)
{
	ll res = 1;
	a %= mo;
	while (b)
	{
		if (b & 1) res = (res * a) % mo;
		a = (a * a) % mo;
		b >>= 1;
	}
	return res;
}

int main()
{
	scanf("%d%d",&n,&m);
	x = 1ll * n * n - 1ll * (n - 1) * (n - 2) / 2 - 1;
	ans = 1;
	for (int i = 1; i <= m - n + 1; i ++)
		ans = (ans % mo * (x + 1ll * i) % mo * ksm(1ll * i,mo - 2) % mo) % mo;
	for (int i = 2; i <= n - 2; i ++) ans = (ans * i) % mo;
	printf("%lld",ans);
	return 0;
}

$T3$

$回家$

moreD城的城市轨道交通建设终于全部竣工，由于前期规划周密，建成后的轨道交通网络由 2n 条地铁线路构成，组成了一个 n 纵 n 横的交通网。如下图所示，这 2n 条线路每条线路都包含 n 个车站，而每个车站都在一组纵横线路的交汇处 。出于建设成本的考虑，并非每个车站都能够进行站内换乘，能够进行站内换乘的地铁站共有 m 个，在下图中，标上方块标记的车站为换乘车站。已知地铁运行 1 站需要 2 分钟，而站内换乘需要步行 1 分钟。 你的最后一个作业就是算出，在不中途出站的前提下，从学校回家最快需要多少时间（等车时间忽略不计）。

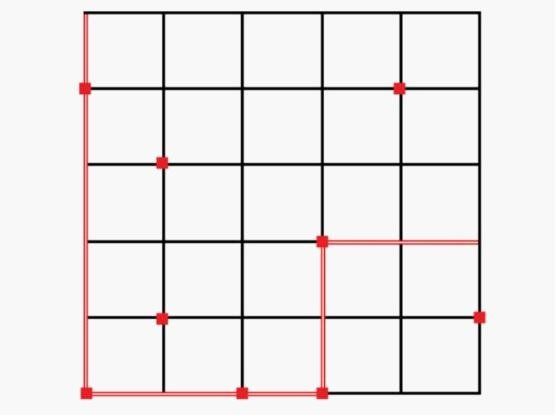
Input
第一行有两个整数 n, m。接下去 m 行每行两个整数 x, y，表示第 x 条横向线路与第 y 条纵向线路的交汇站是站内换乘站。接下去一行是四个整数 x1, y1, x2, y2。表示从学校回家时，在第 x1条横向线路与第 y1 条纵向线路的交汇站上车，在第 x2 条横向线路与第 y2 条纵向线路的交汇站下车。
Output
仅一个整数表示在合理选择线路的情况下，回家所需要的最少时间。如果无法在不出站换车的情况下回家则输出-1.
Sample Input 1
6 9
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
1 1 4 6
Sample Output 1
27

Sample Input 2
6 10
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
6 6
1 1 4 6
Sample Output 2
26

Sample Input 3
2 1
1 2
1 1 2 2
Sample Output 3
5

Data Constraint
对于10%的数据m=0
对于 30%的数据，n ≤ 50, m ≤ 1000；
对于 60%的数据，n ≤ 500, m ≤ 2000；
对于 100%的数据，n ≤ 20000, m ≤ 100000；

其实题目不难，考场一坨人AC，我也不知道为什么考场硬是没把怎么连边给想出来。于是乎，求稳打了个广搜骗分。
考场Code：

#include 
#include 
#include 
using namespace std;

const int maxn = 1e3 + 10;
const int fx[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};
struct Node{
	int x,y,sum,dx;
};
int n,m,w[maxn][maxn][4],x1,y1,x2,y2,ans;
bool v[maxn][maxn];
queue <Node> q;

int read()
{
	int x = 0,w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9') {if (ch == '-') w = -1;ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar();}
	return x * w;
}

int min(int a,int b) {return a < b ? a : b;}

int main()
{
	memset(w,0x3f,sizeof w);
	n = read(),m = read();
	for (int i = 1,x,y; i <= m; i ++)
		x = read(),y = read(),v[x][y] = 1;
	x1 = read(),y1 = read(),x2 = read(),y2 = read();
	q.push(Node{x1,y1,0,0}),q.push(Node{x1,y1,0,1});
	while (!q.empty())
	{
		Node u = q.front();
		q.pop();
		if (v[u.x][u.y])
		{
			for (int i = 0,xx,yy; i <= 3; i ++)
			{
				xx = u.x + fx[i][0];
				yy = u.y + fx[i][1];
				if (xx <= 0 || yy <= 0 || xx > n || yy > n) continue;
				if (i != u.dx && w[xx][yy][i] > u.sum + 3)
				{
					q.push(Node{xx,yy,u.sum + 3,i});
					w[xx][yy][i] = u.sum + 3;
				}
				if (i == u.dx && w[xx][yy][i] > u.sum + 2)
				{
					q.push(Node{xx,yy,u.sum + 2,i});
					w[xx][yy][i] = u.sum + 2;
				}
			}
		} else
		{
			int xx = u.x + fx[u.dx][0],yy = u.y + fx[u.dx][1];
			if (xx <= 0 || yy <= 0 || xx > n || yy > n) continue;
			if (w[xx][yy][u.dx] > u.sum + 2) 
			{
				q.push(Node{xx,yy,u.sum + 2,u.dx});
				w[xx][yy][u.dx] = u.sum + 2;
			}
		}
	}
	ans = min(min(w[x2][y2][0],w[x2][y2][1]),min(w[x2][y2][2],w[x2][y2][3]));
	if (ans == 0x3f3f3f3f) printf("%d",-1); else printf("%d",ans);
	return 0;
}

失败地骗到20分。
靠后经过某些指点，豁然开朗。将同行以和同列的换乘站分别连边，以及终点和起点也连边。然后跑一边Spfa，注意一下纵向和横向的转移时要加一即可。
AC Code

#include 
#include 
#include 
#include 
#define ll long long
using namespace std;

const int maxm = 1e5 + 50;
struct Node{
	int to,next,val,dx;
} f[maxm * 40];
struct Edge{
	int x,y,id;
} g[maxm * 4];
struct Sp{
	int id,dx;
};
int n,m,cnt,head[maxm * 4];
ll dis[maxm * 4][2],ans;
bool vis[maxm * 4][2];
queue <Sp> q;

int read()
{
	int x = 0,w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9') {if (ch == '-') w = -1;ch = getchar();}
	while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar();}
	return x * w;
}

bool cmp1(Edge a,Edge b) {return a.x == b.x ? a.y < b.y : a.x < b.x;}

bool cmp2(Edge a,Edge b) {return a.y == b.y ? a.x < b.x : a.y < b.y;}

ll min(ll a,ll b) {return a < b ? a : b;}

void add(int u,int v,int w,int dx)
{
	f[++ cnt].to = v;
	f[cnt].val = w;
	f[cnt].next = head[u];
	f[cnt].dx = dx;
	head[u] = cnt;
}

int main()
{
	n = read(),m = read();
	for (int i = 1; i <= m; i ++)
		g[i + 1].x = read(),g[i + 1].y = read(),g[i + 1].id = i + 1;
	g[1].x = read(),g[1].y = read(),g[1].id = 1;
	g[m + 2].x = read(),g[m + 2].y = read(),g[m + 2].id = m + 2;
	sort(g + 1,g + m + 3,cmp1);
	for (int i = 1; i <= m + 3; i ++) 
		if (g[i].x == g[i + 1].x) 
		{
			add(g[i].id,g[i + 1].id,2 * (g[i + 1].y - g[i].y),0);
			add(g[i + 1].id,g[i].id,2 * (g[i + 1].y - g[i].y),0);
		}
	sort(g + 1,g + m + 3,cmp2);
	for (int i = 1; i <= m + 3; i ++)
		if (g[i].y == g[i + 1].y) 
		{
			add(g[i].id,g[i + 1].id,2 * (g[i + 1].x - g[i].x),1);
			add(g[i + 1].id,g[i].id,2 * (g[i + 1].x - g[i].x),1);
		}
	q.push(Sp{1,0}),q.push(Sp{1,1});
	vis[1][0] = vis[1][1] = 1;
	memset(dis,0x3f,sizeof dis);
	dis[1][0] = dis[1][1] = 0;
	while (!q.empty())
	{
		Sp u = q.front();
		q.pop();
		vis[u.id][u.dx] = 0;
		for (int i = head[u.id],v; i; i = f[i].next)
		{
			v = f[i].to;
			if (dis[v][f[i].dx] > dis[u.id][u.dx] + 1ll * f[i].val + 1ll * (f[i].dx ^ u.dx))
			{
				dis[v][f[i].dx] = dis[u.id][u.dx] + 1ll * f[i].val + 1ll * (f[i].dx ^ u.dx);
				if (!vis[v][f[i].dx])
				{
					vis[v][f[i].dx] = 1;
					q.push(Sp{v,f[i].dx});
				}
			}
		}
	}
	ans = min(dis[m + 2][0],dis[m + 2][1]);
	if (ans == 0x3f3f3f3f3f3f3f3f) printf("%d",-1); else printf("%lld",ans);
	return 0;
}

总感觉靠后的代码总是好看一些。
$100+0+20$
排名偏低，有能力打$200$分的，以后还要加油， 积累经验。