决策论之朴素贝叶斯(NaiveBayes)
前言
相信学过概率论和数理统计的朋友们都不会对贝叶斯公式感到陌生,其作用可以说是描述了前验概率P(A)和后验概率P(A|B)的关系,又可以说是描述了在事件A发生的条件下发生事件B的概率P(B|A)和在事件B发生的条件下发生事件A的概率P(A|B)之间的关系,因此作用特别广泛。
贝叶斯原公式为:
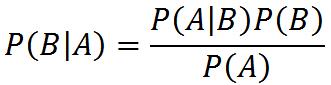
而后由此衍生而来的公式有:
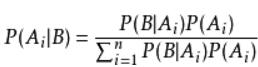 其中Ai (i={1、2、3…n})为一个完备集。
其中Ai (i={1、2、3…n})为一个完备集。
贝叶斯公式的魔力
有这么一个比较好的例子。话说重庆理工大学男女比例为3:2,即P(男)=0.6、P(女)=0.4。经过某领导统计后得知男生穿裙子的概率为0.1,女生穿裙子的概率为0.7,即P(穿裙子|男)=0.1,即P(穿裙子|女)=0.7。这时迎面走来一个穿着翩翩长裙的同学,由于小编眼瞎,只看得见裙子而看不清脸,分辨不出是男是女是否该去搭讪,那博主该如何判断其性别呢?
这时认真上过概率论的博主简单的在心里用贝叶斯公式掂量了一下:

这么一掂量啊,就知道了是男生的概率是0.176,而是女生的概率为0.824。因此博主依靠概率便大胆判断是个女同学,选择前去打望。
生活中不缺少这样的例子。。。
朴素贝叶斯精讲
问题阐述
假设有一个数据集:
每个个体都有特征向量f={f1,f2,f3…fn}
所有个体共有类别变量C={C1,C2,C3…Cm}
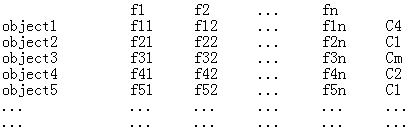
通过数据我们能够很容易的计算出:
每个类别变量的概率P(C1)、P(C2)、P(C3)…P(Cm)
每个特征在每个类别类别下的概率

我们再假设有个待分类的个体feature(x) = {fx1,fx2,fx3…fxn}
所以我们所求的目标应该是每个特征向量在每个类别下的概率P(C1|x)、P(C2|x)、P(C3|x)…P(Cm|x),选出拥有最大概率的类别为我们的预测值。
问题解决
这里就拿P(C1|x)为例子来讲述如何求解吧
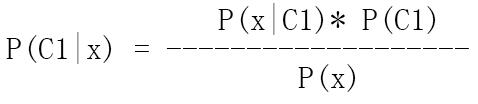
这个公式中P(C1)是已知的,接下来得解决P(x|C1)和P(x)。
这里特别提示!特别提示!特别提示!朴素贝叶斯之所以朴素,是因为他有一个非常重要的前提:假设特征间两两独立,请朋友们在心里默念3遍哦~所以有以下等式成立:


而在P(x)的等式中,我们该如何求解每个P(fxi) 呢?

所以最后综合起来就是

针对离散型的特征变量
针对连续型的特征变量
这里我们就得假设该连续型特征变量为正态分布了,然后我们用正态分布区拟合再通过函数去求x值所对于的y值。
影响算法准确率的因素探究
以下我们以训练集的数量为自变量探究探究训练集的数量对准确率的影响
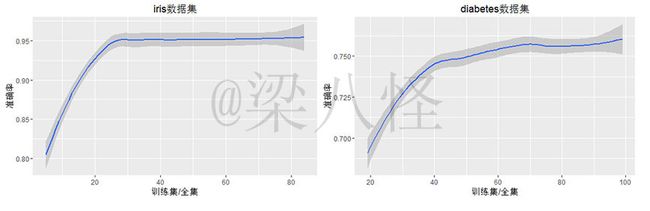
由图可知,当训练集较少时,准确率不高,但是随着训练集的增加,准确率越来越高,直到到达某值(最大值)后,准确率趋于稳定,不再随着训练集的增加而增加。
在图三有两个很重要的点
①准确率最大值Y0
②准确率达到最大时的训练集/全集值X0
那么影响X0和Y0的因素有哪些呢?
有待博主研究☺☺☺
代码
klaR包和e1071中都有自带的naiveBayes函数,大家可以用它建立贝叶斯规则后predict去决策分类。而以下则是博主自己写的代码,毕竟博主是计算机专业出生的嘛,有什么算法都想亲自写写。
naive_bayes<-function(train_data,test_data){#train_data为训练集,默认最后一列为类别项
p_category<-prop.table(table(train_data[,ncol(train_data)]))#每个类别变量概率
pro<-apply(test_data, 1, function(x){#针对每个训练集计算
tops<-buttoms<-c()#初始化分子分母序列
for (category in names(p_category)) {#针对每个类别计算
temp<-train_data[train_data[,ncol(train_data)]== category,]#过滤类别条件
top<-p_category[category]#初始化分子
buttom<-1#初始化分母
for (feature in 1:ncol(test_data)) {#针对每个特征
if (!is.na(x[feature])){#过滤NA值
if (class(train_data[,feature]) == 'numeric' || class(train_data[,feature]) == 'integer') {
top<-top * dnorm(x = as.numeric(x[feature]),mean = mean(temp[,feature],na.rm = T),sd = sd(temp[,feature],na.rm = T))#计算分子
sum<-0#计算分母
for (c in names(p_category)) {
t<-train_data[train_data[,ncol(train_data)]== c,]#过滤类别条件
sum<-sum + dnorm(x = as.numeric(x[feature]),mean = mean(t[,feature],na.rm = T),sd = sd(t[,feature],na.rm = T)) * p_category[c]
}
buttom<-buttom * sum
}else{
top<-top * prop.table(table(temp[,feature]))[x[feature]]#计算分子
sum<-0#计算分母
for (c in names(p_category)) {
t<-train_data[train_data[,ncol(train_data)]== c,]#过滤类别条件
sum<-sum + prop.table(table(t[,feature]))[as.character(x[feature])] * p_category[c]
}
buttom<-buttom * sum
}
}
}
tops<-c(tops,top)#加入分子队列
buttoms<-c(buttoms,buttom)#加入分母队列
}
return(tops/buttoms)
})
pro<-as.data.frame(t(pro))#转换为数据框
pro$category<-apply(X = pro,MARGIN = 1,FUN = function(x){
return(colnames(pro)[which(x == max(x))])
})
return(pro)
}