基于比较的三种稳定排序算法

本文主要介绍三种常见基于比较且稳定排序算法基本原理和实现 ，以及排序算法的性能分析。

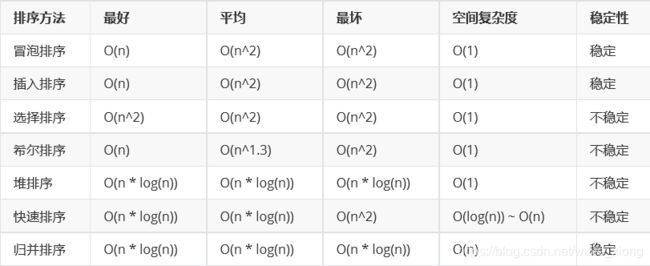
常见的基于比较的排序算法有如下七种

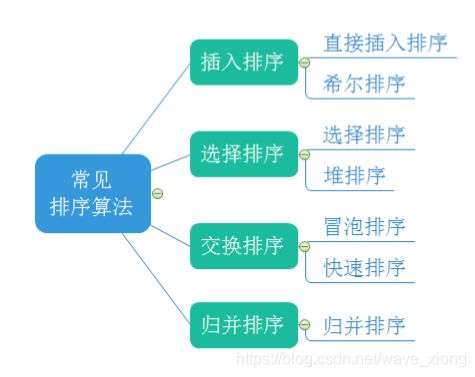
其中稳定的排序算法只有直接插入排序，冒泡排序和归并排序。其余5种都是不稳定排序。关于排序的稳定性，举个例子
一组数据排序排序前为
10，15， 5， 6（a），7 ，6（b）
排序后：
5 ，6(a)， 6(b).，7， 10， 15
对于相等的数据，如果经过排序后，排序算法总能保证其相对位置不发生变化，则我们称该算法是具备稳定性的排序算法。
如果一个排序算法是不稳定的，我们是无法将其优化为稳定排序的。

1.直接插入排序

将数组分为有序和无序两块，初始的有序区间为排序数组的第一个值，其后的为无序区间。
每次取无序区间的第一个值向前比较然后插入，插入位置以后的元素下标后移1。
最坏情况下： 时间复杂度为O(n^2) 无序的时候
最好情况下： 时间复杂度为O(n) 有序的时候
空间复杂的为O(1)
越有序越快。

public static void insertSort1(int[] array) {
     //直接插入排序
        for (int i = 1; i < array.length; i++) {
     
            int tmp = array[i];
            int j = i-1;
            for (; j >= 0 ; j--) {
     
                if(array[j] > tmp) {
     
                    array[j+1] = array[j];
                }else {
     
                    break;
                }
            }
            array[j+1] = tmp;
        }
    }

我们能发现直接插入排序在选择无序区间的一个元素后，是依次与之前的元素比较然后插入，当数组较大时，一个数在插入前可能需要比较很多次，这里我们是可以用二分查找的思路进行优化的，即每次选择与有序区间中间一个数比较，可以有效减少比较次数。有兴趣可以自己动手试试。

2.冒泡排序

冒泡排序的原理：依次比较相邻下标的两位的数值，然后进行排序，每一躺确定一个最大的数，将其放在数组最后。之前有写过一篇博文详细介绍冒泡的过程
冒泡排序https://blog.csdn.net/wave_xiong/article/details/102627782
最坏情况下： 时间复杂度为O(n^2) 无序的时候
最好情况下： 时间复杂度为O(n) 有序的时候
空间复杂的为O(1)
这里附上代码

public static void bubbleSort(int[] arr) {
     
for (int j = 0; j < arr.length-1; j++) {
     //控制趟数
boolean flag=false；
for (int i = 0; i < arr.length - j-1; i++) {
     //控制每趟次数
    if (arr[i] >= arr[i + 1]) {
     
        int tmp = arr[i];
        arr[i] = arr[i + 1];
        arr[i + 1] = tmp;
        flag = true;
 			}
		}
	if(!flg) {
     
    		break;
		}
	}
}

3.归并排序

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将两个有序表合并成一个有序表的过程称为二路归并
归并排序的排序过程为：
先将无序序列拆分成一个个小序列，然后在合并的过程中将其排序，最后的到一个有序的序列。
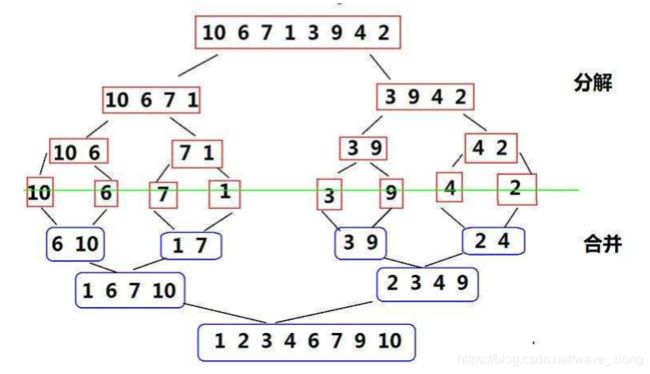
例如对于{10，6，7，1，3，9，4，2}这样一个序列，归并排序的过程如下图

要实现归并排序，我们需要解决几个问题
1.如何将序列拆分成一个个元素，
2.如何保证连接的两个有序序列最终有序

对于这种做重复操作的算法，一般都是用递归来实现
第一步，拆分序列

private static void mergeDivide(int[] array, int first, int last) {
     

        if (first == last) {
       		//递归的终止条件
            return;
        }

        int mid = (first + last) / 2;
        mergeDivide(array, first, mid);
        mergeDivide(array, mid + 1, last);
        //拆分完之后进行合并
        merge(array, first, mid, last);
    }

2.排序并合并函数merge

private static void merge(int[] array, int first, int mid, int last) {
     
        int s1 = first;//第一个区间的起始元素
        int s2 = mid + 1;//第二个的起始元素
        //数组长度
        int len = last - first+ 1;//数组长度
        
        int[] tmp = new int[len];//合并后元素存放的位置
       
        int k = 0;//tmp数组的下标
        while (s1 <= mid && s2 <= last) {
     //两个区间都有元素时
            //array[s1] < array[s2]就是不稳定的排序
            if (array[s1] <= array[s2]) {
     
                tmp[k] = array[s1];
                k++;
                s1++;
                //写成tmp[k++] = array[s1++]也行
            } else {
     
                tmp[k] = array[s2];
                k++;
                s2++;
            }
        }
        // 上面的循环结束之后, 两个区间至少有一个是遍历完了的.
        while (s1 <= mid) {
     //s2已大于last
            tmp[k] = array[s1];
            k++;
            s1++;
        }
        while (s2 <= last) {
     //s1已大于mid
            tmp[k] = array[s2];
            k++;
            s2++;
        }
        //合并，将临时数组的元素给原数组
		
        for (int j = 0; j < tmp.length; j++) {
     
            array[first + j] = tmp[j];
        }
    }

for (int j = 0; j < tmp.length; j++) {
array[first + j] = tmp[j];
}

这一句是归并排序的难点，由于递归的存在，各时段tmp数组的长度都不相同，如何才能保证排好序的元素放回原序列时，它的下标区间不变。

最后调用

 public static void mergeSort(int[] array){
     
        mergeDivide(array,0,array.length-1);
    }

时间复杂度为O(n*log2（n）)
时间复杂度为O(n)

数据结构排序的这部分，学习时必须要动手画图，明白排序时元素到底是如何移动以及怎样变有序的。只有这样才能理解代码，才能真正自己动手完成代码。

另附一张排序性能的汇总表