L1、L2 正则项详解 - 解空间、先验分布、最大似然估计 and 最大后验估计

• 引入

  在线性回归或其他模型中，我们经常使用正则项，例如：对普通线性回归添加 L₁ 正则项后就变为 Lasso 回归，对普通线性回归添加 L₂ 正则项后就变为 Ridge 回归。对于正则项，我们都知道 L₂ 正则项具有缩放型效应，可以让模型参数更加平滑；L₁ 正则项具有截断型效应，使得模型参数更加稀疏。那么本文就对这现象的背后原理进行讲解。

• 直观看

  首先对平滑与稀疏建立一个直观的概念，稀疏意味着使模型参数等于 0，从而在模型内部嵌入式地进行特征选择,；而平滑则会尽量使参数小，但不等于 0，从而嵌入式地对特征进行缩小。

  举一个不严谨但直观简单的例子，方便理解：设$f(x;w)$为经验损失，$L$ 代表正则项，$l(x;w)=f(x;w)+L$ 为结构损失。假设此时使用梯度下降更新参数，$\mu$ 为学习率，则梯度为 $\mu \frac{\partial f(w)}{\partial w_i}-\mu \ast \frac{\partial L}{\partial w_i}$，对于不同的正则项 $\mu \frac{\partial f(w)}{\partial w_i}$ 是相同的，我们暂时忽略，所以：

  1. 使用 L₁ 正则项，梯度为：$\mu \frac{\partial {\sum }_{i=1}^n|w_i|}{\partial w_i}=\mu \ast 1=\mu$， 梯度更新参数的表达式为：$w_i:=w_i-\mu \ast 1$，假设 $\mu =0.5$，则 $w_i:=w_i-0.5$，所以 L₁ 意味着在更新参数时相当于一直减去一个定值，那么终会有一时刻将 $w_i$ 减为 0，那么此时参数为 0，所以稀疏。
  2. 使用 L₂ 正则项，梯度为：$\frac{1}{2}\mu \frac{\partial {\sum }_{i=1}^n(w_i{)}^2}{\partial w_i}=\mu w_i$， 梯度更新参数的表达式为：$w_i:=w_i-\mu w_i$，假设 $\mu =0.5$，则 $w_i:=w_i-\frac{1}{2}{w}_i:=\frac{1}{2}{w}_i$，相当于每次的更新都是折半，则更新的图像为 ${\log }_2{w}_i$，所以只会趋近于 0，不会等于 0，趋于平滑。

  通过上面不正规的例子，我们对稀疏性与平滑型有了直观的理解，下面就开始正式的通过公式证明。

• 解空间

  在优化过程中，我们希望在优化经验损失 ${\sum }_{i=1}^n(y_i-w^T{x}_i{)}^2$ 的同时，还希望对模型的复杂度进行限制，约束参数的取值空间，从而达到防止过拟合的效果，那么我们可以为优化问题加上一个约束，即参数 $w$ 的范数不能大于 C：

  对于 L_β 范数：$\{\begin{array}{l}min{\sum }_{i=1}^n(y_i-w^T{x}_i{)}^2\\ s.t.||w|{|}_{\beta }-C\le 0，\beta =1,2\end{array}$

  为了求解带约束条件的凸优化问题，写出拉格朗日函数：

  $L(x,w,\lambda )={\sum }_{i=1}^n(y_i-w^T{x}_i{)}^2+\lambda (||w|{|}_{\beta }-C)$

  假设此时 $w^{\ast },{\lambda }^{\ast }$ 为原始问题与对偶问题的最优解，则根据 $KKT$ 条件，应分别满足：

  $\{\begin{array}{l}{\nabla }_{w}L(x^{\ast };w^{\ast };{\lambda }^{\ast })=0\\ {\nabla }_{\lambda }L(x^{\ast };w^{\ast };{\lambda }^{\ast })=0\\ \lambda (||w|{|}_{\beta }-C)=0\\ {\lambda }^{\ast }\ge 0\\ ||w|{|}_{\beta }-C\le 0\end{array}{}_{⟹}^{其中}\{\begin{array}{l}{\nabla }_w[{\sum }_{i=1}^n(y_i-{w^{\ast }}^T{x}_i^{\ast }{)}^2+{\lambda }^{\ast }(||w^{\ast }|{|}_{\beta }-C)]=0\\ {\lambda }^{\ast }\ge 0\end{array}$

  回头看，${\nabla }_w[{\sum }_{i=1}^n(y_i-{w^{\ast }}^T{x}_i^{\ast }{)}^2+{\lambda }^{\ast }(||w^{\ast }|{|}_{\beta }-C)]=0$ 表示的就是： $w^{\ast },{\lambda }^{\ast }$ 为带有正则项的优化问题的最优解的条件，且 ${\lambda }^{\ast }$ 为正则项前的正则参数。与我们通常使用的结构损失正好对应！

  对于正则项前的系数 $\lambda$，用来控制经验损失与正则项的相对重要性，$\lambda$ 值越大，表明正则项越严格，更倾向于获得稀疏模型。

  由以上我们可以得出：加入正则项就相当于对经验损失加上约束条件，从而变成约束优化问题。对应于解空间来讲，有下图：
  

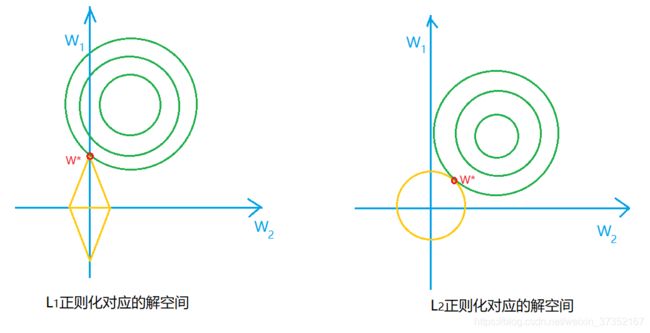
  对于解空间我们可以想象到 2 维的情景，假设在 $w_1,w_2$ 的解空间中，菱形与圆形分别对应 L₁ 与 L₂ 中 $w_1,w_2$ 取值范围，$w^{\ast }$ 为 $w$ 的最优解（L₁ 正则是绝对值之和，可以认为是一次函数类似 $a{w}_1+b{w}_2=0$ 围城的图形，所以是菱形；L₁ 正则是平方之和，可以认为是二次函数类似 $(w_1{)}^2+(w_2{)}^2=0$ 围城的图形，所以是圆形）。

  如果原问题目标函数的最优解不是恰好落在解空间内，那么约束条件下的最优解必然在解空间与约束空间的交点处。L₁ “棱角分明”的约束空间更容易与解空间在角点碰撞，且 L₁ 中两个参数值倾向于一个较大另一个为 0，L₂ 中两个参数倾向于均为非零的较小数（使用 L₂ 正则项时，只有当解空间的中心与 L₂ 约束空间的中心垂直或平行时才能得到一个参数为 0，另一个参数较大，而 L₁ 的约束空间则不然）。所以就有 L₁ 稀疏，L₂ 平滑的效果。

• 先验分布

  如果在概率估计的范畴，则可以通过先验分布解释 L₁ 与 L₂ 的稀疏性与平滑性。

  在从先验分布角度介绍 L₁，L₂ 之前，我们先了解一下最大似然估计与最大后验估计（参考链接）。

  1. 最大似然估计

     对于函数 $P(x|\theta )$，有两个输入，$x$ 表示已知数据，$\theta$ 表示条件参数，那么这个条件概率可以从两个方面理解：

     $\bullet$ 如果 $\theta$ 已知，$x$ 未知，这个函数称为概率函数，用于计算对于不同 $x$ 发生的概率；

     $\bullet$ 如果 $x$ 已知，$\theta$ 未知，这个函数称为似然函数，用来描述，当样本数据发生的经验概率（可从数据中统计）是已知，计算使它产生这样经验概率的参数是多少（似然，可以认为是接近真实，近似它自然拥有的参数）。

     最大似然估计的计算过程：

     例：此时抛硬币10次，其中正面 7 次，反面 3 次，设 硬币正面出现的概率为 $\theta$， 请估计硬币正面出现的概率。

     ① 写出 似然函数：$f(x)={\theta }^7(1-\theta {)}^3$

     ② 转换成 对数似然函数：$\ln f(x)=\ln ({\theta }^7(1-\theta {)}^3)=7\ln \theta +3\ln (1-\theta )$

     ③ 对 $\theta$ 求导，并令导数等于 0：$\frac{7}{\theta }-\frac{3}{1-\theta }=0$，解得 $\theta =0.7$

     （④ 对于更加复杂的函数形式可使用梯度下降）

  2. 最大后验估计

     最大后验估计运用贝叶斯公式：$P(w|X)=\frac{P(X|w)P(w)}{P(X)}$，是在最大似然估计的基础上加入了先验概率。

     其中 $X$ 作为已知的训练数据出现，最大似然估计的目的是最大化 $P(w|X)$，即在已知数据的基础上既最大化似然函数 $P(X|w)$，又要最大化 $P(w)$。意味着要考虑先验概率 $P(w)$ 。与之前文章讲的贝叶斯公式（机器学习 - 朴素贝叶斯（上）- 概率论基础）可视为一样的：我们先对参数 $w$ 计算先验概率，而后通过数据计算条件概率 $P(X|w)$ 对先验概率进行修正。

  现在我们可以根据最大后验估计对 L₁ 与 L₂ 的稀疏与平滑进行解释了。

  对于机器学习模型，我们都是已知数据对参数进行学习，相当于对 $w$ 进行估计，此过程可用最大后验估计表示，其中 $X,Y$ 为数据及其标签：

  $P(w|X,Y)=\frac{P(X,Y|w)P(w)}{P(X,Y)}$

  根据最大后验估计，我们的目标是最大化 $P(X,Y|w)$ 以及 $P(w)$，而对于同一个任务，所使用的数据是不变的，所以 $P(X,Y)$ 可以视为常数忽略，此时最大后验估计可表示为：

  $P(w|X,Y)=P(X,Y|w)P(w)$

  同样取对数，得对数后验函数：

  $f(x)=\log (P(X,Y|w)P(w))=\log P(X,Y|w)+\log P(w)$

  从中可以发现：对数后验函数是在对数似然函数的基础上增加了 $\log P(w)$，其中 $P(w)$ 的意义是对参数 $w$ 的概率分布做出的先验假设，在收集到训练数据 $X,Y$ 后，则可根据 $w$ 在 $X,Y$ 下的条件概率对 $w$ 进行修正，从而做出对 $w$ 进行更好地估计。

  $\bullet$ 若假设 $w_j$ 的先验分布为 0均值 的高斯分布，即：$w_j\sim N(0,{\sigma }^2)$

  $\log P(w)=\log {\prod }_{j}P(w_j)=\log {\prod }_j[-\frac{1}{\sqrt{2\pi }{\sigma }^2}{e}^{-\frac{(w_j{)}^2}{2{\sigma }^2}}]=-\frac{1}{2{\sigma }^2}{\sum }_j{w}_j^2+C^{\prime }$

  很巧，在高斯分布下，$\log P(w)$ 具有 ${\sum }_j{w}_j^2$ 项 ，与 L₂ 正则项是效果等价的。

  所以使用 L₂ 正则项相当于对模型参数 $w$ 引入了高斯先验。

  $\bullet$ 若假设 $w_j$ 服从 均值为0，参数为 $a$ 的拉普拉斯分布，即：$P(w_j)=\frac{1}{\sqrt{2a}}{e}^{\frac{-|w_j|}{a}}$

  $\log P(w)=\log {\prod }_{j}P(w_j)=\log {\prod }_j\frac{1}{\sqrt{2a}}{e}^{\frac{-|w_j|}{a}}=-\frac{1}{a}{\sum }_j|w_j|+C^{\prime }$

  很巧，在拉普拉斯分布下，$\log P(w)$ 具有 ${\sum }_j|w_j|$ 项 ，与 L₁ 正则项是效果等价的。

  所以使用 L₁ 正则项相当于对模型参数 $w$ 引入了拉普拉斯先验。

  但是高斯先验为什么会使参数更平滑而拉普拉斯为什么会使参数更稀疏呢？

  首先来看阿门两个分布函数的图像：
  
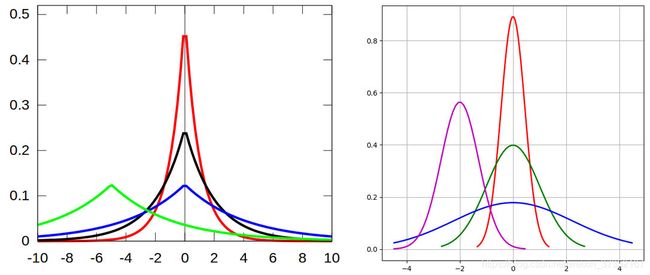
  （左图为拉普拉斯分布，右图为高斯分布，图片来自网络。）

  对于拉普拉斯分布，大部分概率分布都聚集在 0 附近，而对于值较大的概率较小，所以获得 $w=0$ 的概率更高，从而更倾向于稀疏；而对于高斯分布，其中取值较大的概率的分布相比拉普拉斯分布更大，而在 0 附近的概率分布较小，所以对于 $w=0$ 的概率更小，所以更倾向于平滑。