《Adaptive Graph Convolutional Neural Networks》论文理解
1.AGCN模型框架
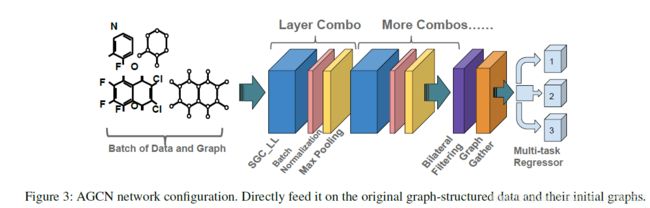
AGCN由多个连续层组合而成,其核心层为SGC-LL层。层组合包括一个SGC-LL层,一个批处理归一层和一个图最大池化层。在每个SGC-LL层训练残差图Laplacian,并在接着一层图池层。在下一个SGC-LL层之前,自适应图(固有+残差图)一直被重用,因为SGC-LL会变换特征,所以下一个SGC-LL需要重新训练一个新的残差图。
在进过上述组合层(SGC-LL层,批处理归一层,图最大池化层)后,批处理的图形结构将被更新,而图形大小保持不变。由于任何图像粗化或特征平均都将破坏信息性局部结构的完备性。所以,最大池化的时候不跳过任何顶点。如果对网络进行图预测任务,图聚合层是将是最后一层。
2.SGC-LL Layer
SGC-LL Layer是这篇论文的主要工作,它对《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》 中的ChebNet模型进行了改善。作者认为,图的拓扑结构是固有的,它仅仅表示物理连接,不能充分表达出针对特定任务的所有有意义的拓扑结构,但是,原始的拉普拉斯矩阵依然包含了大量有用的图结构信息;所以设计出可学习的残差图拉普拉斯矩阵来调整原始的拉普拉斯矩阵,使得新的拉普拉斯矩阵包含那些无法直接在原始的图上学习到的由虚拟顶点连接组成的子结构。残差图拉普拉斯矩阵表示的子结构如下图中AGCN的虚线所示:

公式标号按照论文《Adaptive Graph Convolutional Neural Networks》中一样,所以标号有跳跃。
归一化拉普拉斯矩阵:
L = I − D − 1 / 2 A D − 1 / 2 (2) L=I-D^{-1/2}AD^{-1/2}\tag2 L=I−D−1/2AD−1/2(2)
C h e b N e t ChebNet ChebNet中的图卷积公式:
y = g θ ( L ) X g θ ( L ) ≈ ∑ k = 0 K − 1 θ k T k ( L ~ ) L ~ = 2 L / λ m a x − I n (3) \begin{aligned} &y=g_{\theta}(L)X\\ &g_{\theta}(L)\approx\sum_{k=0}^{K-1}\theta_{k}T_{k}(\tilde{L})\\ &\tilde{L}=2L/\lambda_{max}-I_{n} \end{aligned}\tag3 y=gθ(L)Xgθ(L)≈k=0∑K−1θkTk(L~)L~=2L/λmax−In(3)
对于图结构数据,连通节点之间的相似度可能低于未连通节点,所以欧氏距离已不再是度量顶点相似性的好的度量指标。
作着利用泛化的马氏距离作为相似性度量指标:
D ( x i , x j ) = ( x i − x j ) T M ( x i − x j ) (6) D(x_i,x_j)=\sqrt{(x_i-x_j)^TM(x_i-x_j)}\tag6 D(xi,xj)=(xi−xj)TM(xi−xj)(6)
其中 M M M为对称的半正定矩阵,对称矩阵都可以分解成矩阵和矩阵转置的乘积,即 M = W d W d T M=W_dW_d^T M=WdWdT,所以 W d ∈ R d × d W_d\in R^{d\times d} Wd∈Rd×d为SGC-LL Layer的训练参数。然后利用该距离计算高斯核:
G x i , x j = e x p ( − D ( x i , x j ) / ( 2 σ 2 ) ) (7) G_{x_i,x_j}=exp(-D(x_i,x_j)/(2\sigma^2))\tag7 Gxi,xj=exp(−D(xi,xj)/(2σ2))(7)
将矩阵 G G G归一化后就得到了残差图拉普拉斯矩阵对应的邻接矩阵 A ^ \hat A A^。将其带入公式(1)可以得到归一化残差图拉普拉斯矩阵 L ^ \hat L L^。
虽然直接利用 L ^ \hat L L^带入公式(2)实现图卷积,由于原始的拉普拉斯矩阵依然包含了大量有用的图结构信息,并且为了加速训练和提高学习到的拓扑结构的稳定性,所以使得 L ^ \hat L L^作为残差图拉普拉斯矩阵以加权系数的方式与原始的拉普拉斯矩阵 L L L相加,得到新的拉普拉斯矩阵 L ^ \hat L L^。
L ^ = L + α L r e s (9) \hat L=L+\alpha L_{res}\tag9 L^=L+αLres(9)
其中 L r e s L_{res} Lres表示归一化残差图拉普拉斯矩阵。
在利用 L ^ \hat L L^带入公式(2)计算图卷积后,作者认为在图卷积是不同顶点的同一特征创建和训练单独的拓扑结构,在经典的CNN网络中,卷积层的输出特征是最后一层的所有特征图的和,这些特征图是由独立的滤波器计算出来的,所以新特性不仅建立在相邻的顶点上,而且还依赖于顶点内特征。为了构造顶点内和顶点间特征的映射,在图卷积后加上了一层全连接层:
Y = ( g θ ( L ^ ) X ) W + b (8) Y=(g_{\theta}(\hat L)X)W+b\tag8 Y=(gθ(L^)X)W+b(8)
3.Graph Max Pooling
图最大池化是按特征进行的,取该节点和它邻域节点特征的最大值来更新节点的特征值:
x ^ v ( j ) = m a x ( x v ( j ) , x i ( j ) , ∀ i ∈ N ( v ) ) \hat x_v(j)=max({x_v(j),x_i(j),\forall i\in N(v)}) x^v(j)=max(xv(j),xi(j),∀i∈N(v))
4.Graph Gather
图聚合层逐节点对所有的顶点特征向量求和作为图数据的表示。聚合层的输出向量将用于图级预测。没有图形收集层,AGCN也可以训练和用于顶点的预测任务,给定的标签上的顶点。顶点方面的预测包括社交网络等方面的许多预测。
5.Bilateral Filter
在AGCN中使用双边滤波器层的目的是防止过度拟合。 残差图Laplacian肯定会适应模型以更好地适合训练任务,但是存在过度拟合的风险。 为了减轻过度拟合,我们引入了经过修正的双边滤波层,通过增加拉普拉斯矩阵L的空间局部性来规范SGC-LL层的激活,同时引入了批量归一化层以加快训练速度。
