汉诺塔问题(递归写法)
汉诺塔问题是一个很经典的题目

哈哈,其实就是我们都已经很熟悉游戏规则了,在此我就在啰嗦一遍题目。

题目描述:
给定一个由n个圆盘组成的塔,这些圆盘按照大小递减的方式套在第一根柱上。现要将整个塔移动到第三根柱上,每次只能移动一个圆盘,且较大的圆盘在移动过程中不能放置在较小的圆盘上面。
输入:
输入只有一个正整数n
输出:
接下来每一行输出一步移动步骤。
在此,我们讨论比较一种简单而且很好理解的做法——递归做法,既然递归,我们只要想好递归函数,其它的就交给函数吧。

好了,正经了,我们可以想象除了一个圆盘外最简单的一种情况——两个圆盘(哈哈),这种我们当然都知道了。
第一步:只要把上面的1号从A移动到B。
第二步:把2号从A移动到C。
第三步:再把1号从B移动到C就可以了。
(ps:手绘的图,大家就忍受下吧[委屈])
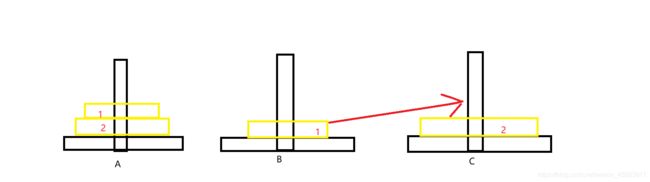
此时,我们想想,我们刚才的步骤是不是就是将两个圆盘从A借助B移动到了C。在我们将1号从A移动到B的时候我们也可以理解成把1号这个圆盘从A借助C移动到B(但是事实我们并没有借助)。这时我们就可以想象了,把那个1号圆盘当做成除了最下面那个圆盘外的(n-1)个圆盘,这时,是不是就豁然开朗了,对于n个圆盘我们一样可以分为三步走[嘻嘻]。
第一步:将(n-1)个圆盘从A借助C移动到B
第二步:将第n个圆盘从A移动到C
第三步:将(n-1)个圆盘从B借助A移动到C
![]()
代码实现下:
void hanoi(int n,char A,char B,char C)
{
if(n==0)
return ;
hanoi(n-1,A,C,B);
step(n,A,C);
hanoi(n-1,B,A,C);
}
另外为了观察,我们还需要写一个打印移动步骤的函数。把id号圆盘从a位置移动到b位置。
上代码:
void step(int id,char a,char b) // 把id号圆盘从a位置移动到b位置
{
cout<<"第"<<cnt++<<"步: 把 "<<id<<"号 从 "<<a<<" 移动到 "<<b<<endl;
}
输出结果:
至于输出的结果当然就是输出:将n个圆盘从A借助B移动到C的步数,也就是 hanoi(n,‘A’,‘B’,‘C’)。
完整代码:
#include共同努力!
Keafmd
