信号转换 | 将对称方波转换成倍频PWM波形
在 信号转换的解题思路 中,提到为了能够使得输出信号的占空比不随着输入信号的频率改变而改变,使用了一种 信号转换| 如何使用模拟电路完成对方波信号倍频PWM转换? 博文中的方式,但是该方式在调试过程中的结果出现了些不太如意的地方。
- 生成的锯齿波的幅值变化范围之后工作电源(+5V)的一半,这也限制了对输入信号频率允许的范围;
- 输出的锯齿波由于诱导肖特基二极管整流的影响,使得顶部出现了平滑,限制 PWM的变化范围;
- 电路过于复杂;
- 输出信号由于受到LMV358的带宽影响,上下沿变化比较缓慢。
本文在前面的基础上,对工作电路进行了改变,特别是采用模拟门来对积分电路电容进行放电,完成锯齿波的转换。
01电路设计1
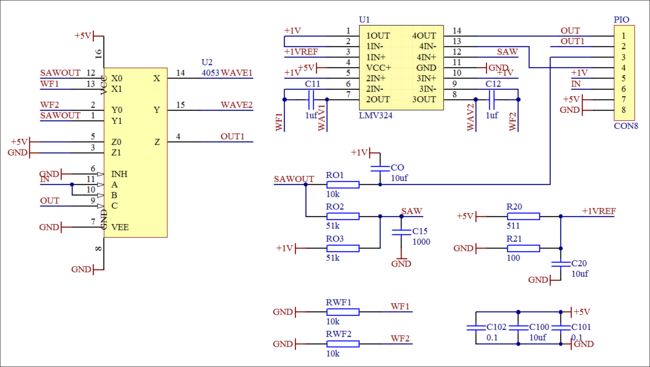
实验电路的原理图如下图所示。
▲ 实验电路的原理图
设计错误:
在最初设计的过程中,原理图中遗漏了RWF1,RWF2两个对于积分电路放电的电阻。需要在后期的调试电路板上进行跳线焊接。
▲ 实验电路PCB
02电路板的调试
1.电路静态参数
- 工作电路 9mA
- 内部参考电压(+1V):0.834V
板内参考电压实际是由 R 20 = 510 Ω R20 = 510\Omega R20=510Ω, R 21 = 100 Ω R21 = 100\Omega R21=100Ω组成分压电阻,所得到的参考电压为: V + 1 V = 100 100 + 510 × 5 V = 0.820 V V_{ + 1V} = { {100} \over {100 + 510}} \times 5V = 0.820V V+1V=100+510100×5V=0.820V
2.动态调试
(1)信号源:
由信号源引入1000Hz的方波信号进入In端口。
▲ 信号源提供的1000Hz的调试方波信号
(2)修正电路中存在的错误
检查运放输出没有波形,发现 设计错误:
在原理图中的WAV1, WAV2被表示成了WAVE1,WAVE2。所以没有实际引线。
修正错误: 手工将WAV1,2连接上。
(3)测量电路中的波形
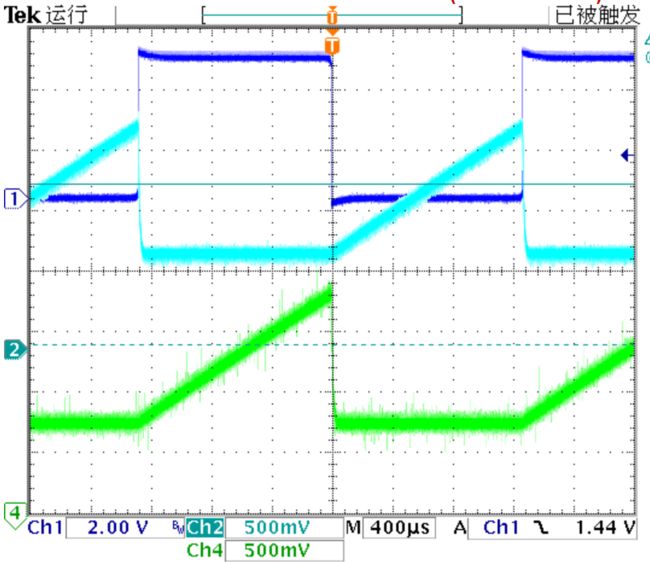
▲ 输入方波信号与积分器的输出
此时输入信号的频率: f i n = 392 H z f_{in} = 392Hz fin=392Hz,半个周期的时间为: T i n 2 = 1 f i n × 1 2 = 1.276 m s T_{in2} = {1 \over {f_{in} }} \times {1 \over 2} = 1.276ms Tin2=fin1×21=1.276ms。
积分器的输入电压,就是班内的参考电压: V + 1 V = 0.820 V V_{ + 1V} = 0.820V V+1V=0.820V。
积分器的输入电阻: R i n = 10 k Ω R_{in} = 10k\Omega Rin=10kΩ,积分电容: C i n t = 0.1 n F C_{ {\mathop{\rm int}} } = 0.1nF Cint=0.1nF。那么在半个周期内的锯齿波的电压峰值为:
V s a w − p = T i n 2 × V + 1 V R i n C i n t = 1.276 × 1 0 − 3 × 0.82 10 × 1 0 3 0.1 × 1 0 − 6 = 1.046 V V_{saw - p} = { {T_{in2} \times { {V_{ + 1V} } \over {R_{in} }}} \over {C_{ {\mathop{\rm int}} } }} = { {1.276 \times 10^{ - 3} \times { {0.82} \over {10 \times 10^3 }}} \over {0.1 \times 10^{ - 6} }} = 1.046V Vsaw−p=CintTin2×RinV+1V=0.1×10−61.276×10−3×10×1030.82=1.046V
实际测量锯齿波的峰值为1.06V,与上面理论计算值相符合。
(4)测量输出合成的锯齿波:
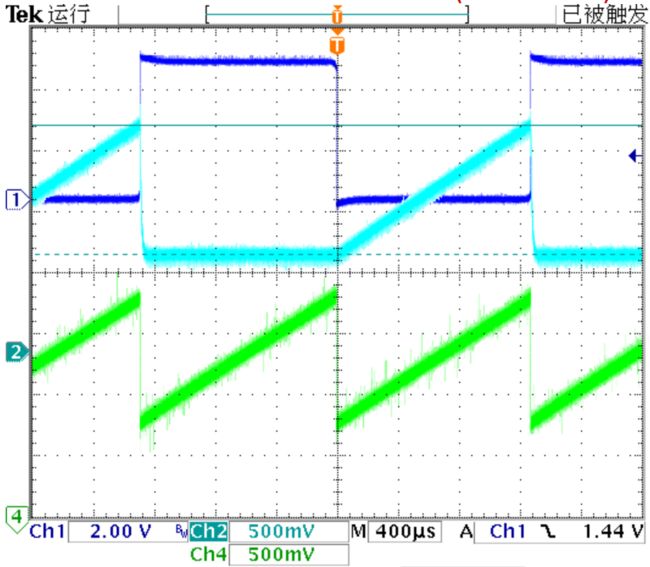
电路中SAWOUT的锯齿波的波形如下:
▲ SAWOUT输出锯齿波信号
将模拟门合成的锯齿波分压一半送到LMV324 OPAM进行比较,对应的波形如下。
▲ SAW(Cyan), SAWOUT(Green)电压波形
(5)输出参考电压
输出的参考电压是由SAWOUT低通滤波之后的数值。
- 测量值为:1.38V
- Vref = 0.823V
幅值为 1.38-0.823=0.557V。这个幅度基本上等于锯齿波的峰值电压的一半。这正是三角锯齿波的平均值与峰值之间的关系。
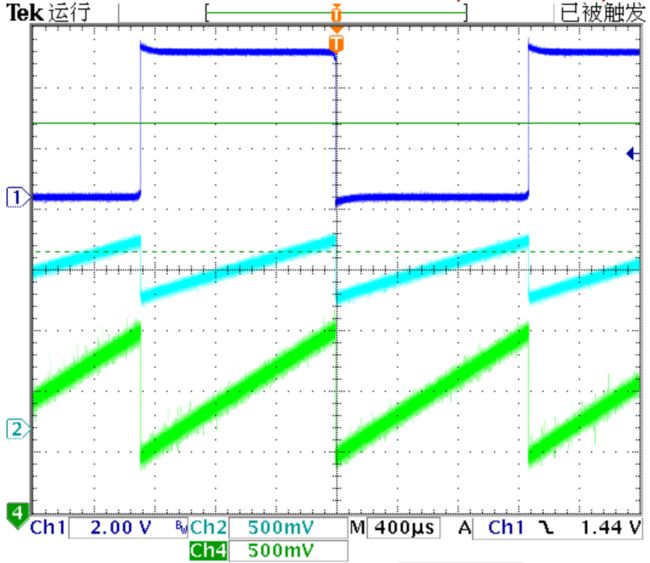
(6)输出PWM波形:
使用一个330k欧姆的电位器,连接在PIO的3,4,5之间,这为最后一级的比较器(运放工作在比较器状态)提供一个参考电压。它的幅值在Vref到SAWOUT的低通滤波器输出的参考电压之间。
下面是最后一级运放输出电压(Cyan)以及它驱动电路中模拟门的Z通道输出的波形(Green)。
▲ 输出PWM波形
03性能测试
下面对该电路的波形变化的性能进行测试。
1.输出PWM的范围
改变外部设定PWM的电位器,可以控制输出波形的PWM占空比。改变占空比的范围在0~100%之间。
▲ 输出PWM波形占空比的范围
2.输出占空比与输入信号频率之间的关系
调节输入信号的频率,观察到输出信号的的占空比变化的情况。
▲ 改变输入信号的频率与输出信号的占空比之间的关系
随着输入信号的频率改变,输出信号的的高电平和低电平在同时改变。
在一定范围内,占空比保持恒定值。但是随着输入频率更大,输出信号的占空比还是发生了一定的改变。
影响输出占空比的原因有两个:
-
如果频率过高,那么内部产生的锯齿波的幅值就过小,那么由最后一级运放比较器的偏执电压,参考电压分压电路的误差等原因,就会造成输出脉冲的占空比的误差增加。
-
如果输入信号的频率过低,使得内部锯齿波出现了饱和,这样也会使得输出波形的占空比出现恨大的误差。
下面显示了输入信号的频率从50Hz~250Hz变化过程中,内部的锯齿波以及输出PWM波形变化的情况。
▲ 频率变化与内部锯齿波波形变化情况
3. 测量输入频率变化对输出占空比的影响
通过测量输出PWM的平均电压,可以测定输出的占空比。
▲ 对电路进行测试
输入频率范围100~1000Hz。
第一个测量是在100Hz的时候设置PWM占空比大约为50%左右,下图显示了随着频率增加,输出PWM的平均电压的变化。
▲ 输入频率与输出PWM平均电压之间的关系
下面是对应的输入、输出信号的变化的情况。
▲ 改变输入信号的频率,测量输出PWM的占空比
▲ 输入信号的频率对输出PWM平均电压的影响
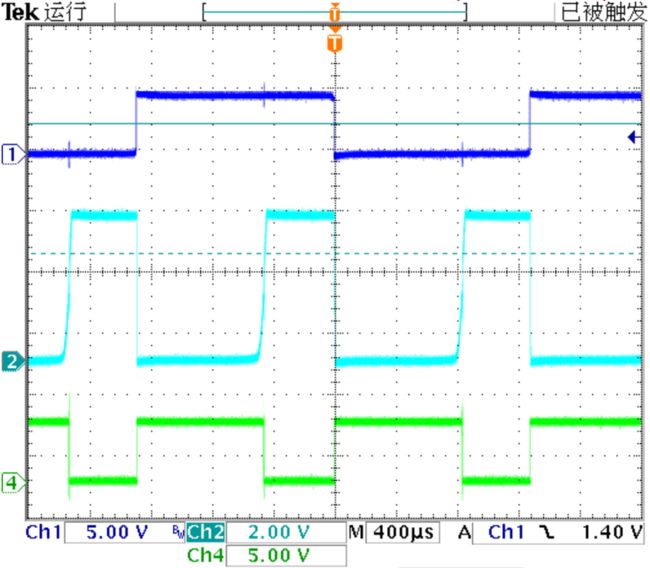
▲ 输入信号频率变化对输出PWM波形的影响
▲ 输入信号的频率对输出PWM的平均电压的影响
▲ 输入信号的频率对于输出PWM波形的影响
将前面三个测量的PWM输出电压随着输入信号频率变化绘制在一张图中进行对比,可以看到输入信号的频率对于PWM的占空比的影响在不同的占空比下的情况还是有区别的。但在输入信号频率在100~1000Hz变化内,PWM信号占空比变化幅度都在5%之内。
![]()
▲ 三种不同PWM占空比的情况下,输入信号的频率对于输出PWM的平均电压的影响
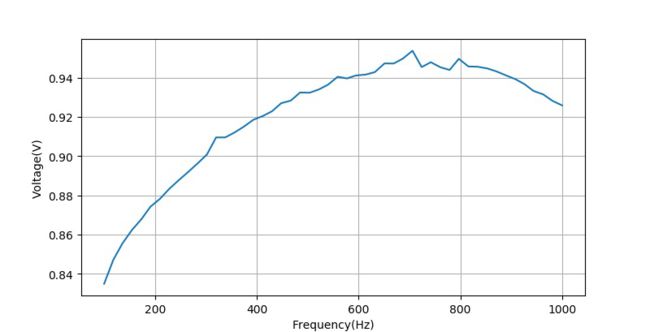
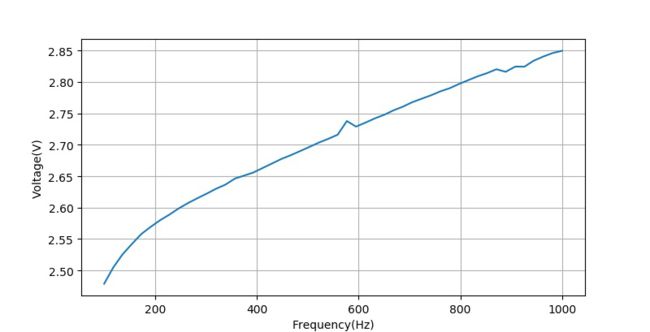
测量不同频率下的输出PWM信号平均电压的数据如下:
f=[100.00,118.00,136.00,155.00,173.00,191.00,210.00,228.00,246.00,265.00,283.00,302.00,320.00,338.00,357.00,375.00,393.00,412.00,430.00,448.00,467.00,485.00,504.00,522.00,540.00,559.00,577.00,595.00,614.00,632.00,651.00,669.00,687.00,706.00,724.00,742.00,761.00,779.00,797.00,816.00,834.00,853.00,871.00,889.00,908.00,926.00,944.00,963.00,981.00,1000.00]
d=[2.48,2.50,2.53,2.54,2.56,2.57,2.58,2.59,2.60,2.61,2.61,2.62,2.63,2.64,2.65,2.65,2.66,2.66,2.67,2.68,2.68,2.69,2.70,2.70,2.71,2.72,2.74,2.73,2.74,2.74,2.75,2.75,2.76,2.77,2.77,2.78,2.79,2.79,2.80,2.80,2.81,2.81,2.82,2.82,2.82,2.82,2.83,2.84,2.85,2.85]
f=[100.00,118.00,136.00,155.00,173.00,191.00,210.00,228.00,246.00,265.00,283.00,302.00,320.00,338.00,357.00,375.00,393.00,412.00,430.00,448.00,467.00,485.00,504.00,522.00,540.00,559.00,577.00,595.00,614.00,632.00,651.00,669.00,687.00,706.00,724.00,742.00,761.00,779.00,797.00,816.00,834.00,853.00,871.00,889.00,908.00,926.00,944.00,963.00,981.00,1000.00]
d=[4.28,4.26,4.23,4.22,4.21,4.21,4.21,4.20,4.21,4.21,4.21,4.21,4.21,4.22,4.22,4.22,4.23,4.23,4.24,4.24,4.24,4.25,4.25,4.26,4.26,4.26,4.27,4.27,4.27,4.28,4.28,4.28,4.29,4.30,4.30,4.30,4.28,4.31,4.32,4.32,4.32,4.33,4.33,4.34,4.34,4.34,4.34,4.36,4.36,4.36]
f=[100.00,118.00,136.00,155.00,173.00,191.00,210.00,228.00,246.00,265.00,283.00,302.00,320.00,338.00,357.00,375.00,393.00,412.00,430.00,448.00,467.00,485.00,504.00,522.00,540.00,559.00,577.00,595.00,614.00,632.00,651.00,669.00,687.00,706.00,724.00,742.00,761.00,779.00,797.00,816.00,834.00,853.00,871.00,889.00,908.00,926.00,944.00,963.00,981.00,1000.00]
d=[0.83,0.85,0.86,0.86,0.87,0.87,0.88,0.88,0.89,0.89,0.90,0.90,0.91,0.91,0.91,0.92,0.92,0.92,0.92,0.93,0.93,0.93,0.93,0.93,0.94,0.94,0.94,0.94,0.94,0.94,0.95,0.95,0.95,0.95,0.95,0.95,0.95,0.94,0.95,0.95,0.95,0.94,0.94,0.94,0.94,0.94,0.93,0.93,0.93,0.93]
实验所使用的Python程序如下:
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST11.PY -- by Dr. ZhuoQing 2020-05-23
#
# Note:
#============================================================
from headm import *
from tsmodule.tsvisa import *
from tsmodule.tshardware import *
from tsmodule.tsstm32 import *
from tsmodule.tsdraw import *
#------------------------------------------------------------
ds6104open()
#------------------------------------------------------------
pltgif = PlotGIF()
setf = linspace(100, 1000, 50)
fdim = []
dutydim = []
for f in setf:
zbcmd(bytes('ad9833setfrequency %d'%int(f), 'utf-8'))
time.sleep(1)
meter = meterval()
printf(meter)
fdim.append(int(f))
dutydim.append(meter[0])
x,y1,y2,y3 = ds6104readcal(1,2,3)
plt.clf()
plt.plot(x, y1, label='Input')
plt.plot(x, y2, label='PWM')
plt.plot(x, y3, label='Saw Wave')
plt.xlabel('Time(s)')
plt.ylabel('Wave')
plt.grid(True)
plt.legend(loc='upper right')
plt.draw()
plt.pause(.1)
pltgif.append(plt)
pltgif.save(r'd:\temp\1.gif')
printf("\a")
tspsavenew('data', f=fdim, d=dutydim)
plt.clf()
plt.plot(fdim, dutydim)
plt.xlabel('Frequency(Hz)')
plt.ylabel('Voltage(V)')
plt.grid(True)
plt.show()
#------------------------------------------------------------
# END OF FILE : TEST11.PY
#============================================================
04结论
本文验证了如下两部分的内容:
- 使用模拟门电路可以有效的从输入方波中产生锯齿波信号。其中应用到了模拟门对积分电容进行放电的过程;
- 使用了锯齿波的平均值电压作为占空比控制的参考电压,它可以随着输入信号的频率的变化而变化,进而保证了输出PWM的占空比不随着输入信号频率的变化而改变。在输入信号频率从100Hz改变到1000Hz的过程中,输入PWM占空比的变化不超过5%。
电路的性能还依赖于所使用的器件的性能。本实验中使用了LMV324,主要是看中了在单电源(+5V)工作的简便性。如果想进一步提高电路的性能,可以采用带宽和精度更高的运放完成电路的设计。
实验电路AD工程文件:AD\Teaching\2020\SignalChange\DoublePWM.PcbDoc ↩︎