哈夫曼树和哈夫曼编码应用之图片压缩编码c++实现
本人正在学习数据结构,在前几天做了压缩图片的项目,感觉到有必要分享给大家。因此今天我就分享给大家c语言数据结构有关哈夫曼树压缩图片的项目实现。
一:下面先介绍有关的知识:
1.背景
压缩软件是用特定算法压缩数据的工具,压缩后的文件称为压缩包,可以对其进行解压。那么为什么要用到压缩软件呢?我们都知道,文件是用编码进行存储的,编码要用到字节,而不可避免的一个文件中会出现很多重复的字节,用压缩软件可以减少重复的字节,方便在互联网上实现更快的传输,也可以减少文件在磁盘上的占用空间,常见的压缩软件有rar,zip等。
压缩可以分为无损压缩和有损压缩两种,无损压缩后的文件,经过解压后可以完全恢复到之前的文件,rar,zip等格式都是无损压缩格式,而图片文件jpg,音乐文件mp3都是有损压缩格式。
2.编码介绍
计算机文件是由一个个字节组成的,一个字节有8位二进制编码构成,共有0-255种可能的情况。由于文件中的字节可能会重复出现,可以对不同的字节设计长度不等的编码,让出现次数较多的字节,采用较短的编码,这样可以使文件编码的总长度减少。
3.哈夫曼树和哈夫曼编码
(1)哈夫曼树
有关二叉树的知识这里就不讲解了,大家可以自行学习。这里我们统计文件中256种字节重复的次数作为权值,构造一棵有256个叶节点的二叉树,如果带权路径长度最小,我们称为这样的二叉树为最有二叉树,也叫哈夫曼(Huffman)树。
(2)哈夫曼编码
哈夫曼树从根结点到每个叶子结点都有一条路径,对路径上的分支,约定指向左子树的为0,指向右子树的为1,从根到每个叶子结点路径上的0和1构成的序列就是这个叶节点的哈夫曼编码。
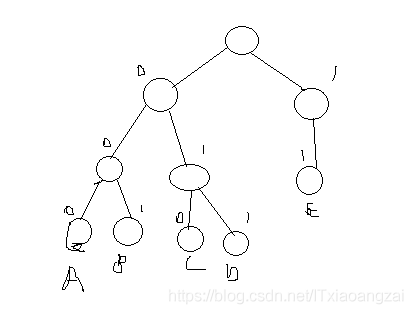
如图所示:
这时编码就是:
A:000 B:001 C:010 D:011 E:11
使用哈夫曼编码给每个字节重新编码,重复次数较多的字节,哈夫曼编码较短,这样就比以前的二进制编码短了许多,因此可以实现压缩。
这里我们实现把一个bmp格式的图片进行压缩编码。
二:过程和代码实现与分析
1.流程简述:
(1)读取文件
先读取文件,生成一棵带权二叉树。树在程序中可以使用顺序结构,链式结构两种方式实现,由于这棵带权二叉树的叶子节点有256个,存储空间是固定的,则这里可以使用顺序结构来表示二叉树。
(2)定义二叉树结构
定义一个结构体HaffNode来表示二叉树的叶子节点,记录每个结点的权值,标记,父结点,左孩子和右孩子。创建一个结构体数组来存储这棵带权二叉树的每个叶子结点的信息。
(3)生成哈夫曼编码
其次,生成Huffman树后,要生成哈夫曼编码,就要先遍历这棵二叉树,这里我用的是先序遍历方法,定义一个字符串数组Code来存储每个叶子结点的哈夫曼编码。
(4)字符串转字节实现压缩
)由于哈夫曼编码是以字符串数组的形式保存的,重新编码后的数据将是一个很长的字符串。定义Str2byte函数,将字符串转化为字节,才能转化为最终的编码,将其保存到*.huf中,则实现了文件压缩。
(5)解压缩
最后,为了保证压缩后的数据能够被正常解压,除了保存压缩的数据,还应保存原文件的长度和256种字节重复出现的次数。这时就需要定义一个文件头,用于保存这些信息,再保存压缩文件时,同时向文件中写入文件头和压缩数据,保证文件能够被还原。
2.代码实现与分析
(1)打开Microsoft Visual Studio 2010,创建一个解决方案,名字为"HuffmanSLN",在HuffmanSLN解决方案下面新建一个空的win32控制台工程,名字为"HfmCompressCPro"。
(2)打开文件
在源文件(Source Files)中新建"main.cpp"文件,作为程序运行的入口函数。
导入
代码如下:
#include
#include
using namespace std;
int main()
{
cout<<"--------------Huffman文件压缩编码---------------"<>filename;
return 0;
} (3)读取原文件
以二进制流的方式,只读打开文件,一个个地逐个读取字节数据,统计文件中256种字节重复出现的次数,保存到一个数组中
int weight[256]中,然后将扫描的结果在控制台打印下来。
代码如下:
#include
#include
using namespace std;
int main()
{
cout<<"--------------Huffman文件压缩编码---------------"<>filename;
char ch;
int weight[256]={0};
//以二进制流的方式打开文件
FILE* in = fopen(filename,"rb");
if(in == NULL)
{
printf("打开文件失败");
return 0;
}
//扫描文件,获得权重
while(ch = getc(in) != EOF)
{
weight[ch]++;
}
//关闭文件
fclose(in);
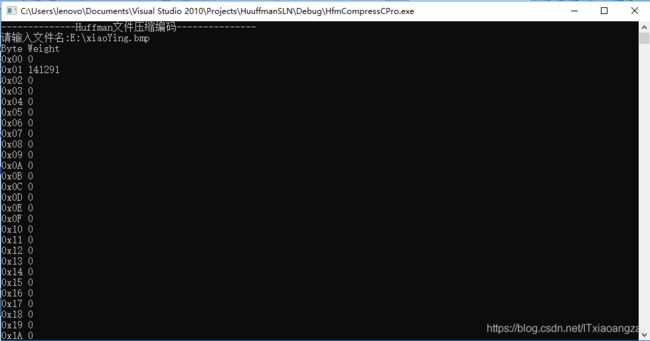
//显示256个字节出现的次数
cout<<"Byte "<<"Weight"< 这里我们的图片在E盘的根目录下:
即下面的一张图:
运行结果如下:
(4)生成哈夫曼树
在Haffman.h文件中,定义一个存储哈夫曼树结点信息的结构体,有权值,标记(若当前结点未加入结构体,flag=0;若当前结点加入结构体,flag=1),双亲结点下标,左孩子结点下标,右孩子结节下标。
在Haffman.cpp文件中创建构造哈夫曼树的函数,在Haffman.h文件中声明。
Haffman.h文件
typedef struct
{
int weight; //权值
int flag; //标记
int parent; //双亲结点下标
int leftChild; //左孩子下标
int rightChild; //右孩子下标
}HaffNode;
//创建叶结点个数为n,权值数组为weight的哈夫曼树haffTree
void Haffman(int weight[],int n,HaffNode haffTree[]);Haffman.cpp文件
#include "Huffman.h"
#define MaxValue 10000
//创建叶结点个数为n,权值数组为weight的哈夫曼树haffTree
void Haffman(int weight[],int n,HaffNode haffTree[])
{
int i,j,m1,m2,x1,x2;
//哈夫曼树haffTree初始化,n个叶结点的二叉树共有2n-1结点
for(i = 0;i < 2 * n - 1;i++)
{
if(i < n) //如果是小于n的结点(叶子结点),则把每个字节的重复次数作为权值赋给这些该结点
haffTree[i].weight = weight[i];
else
haffTree[i].weight = 0; //其他非叶子结点权值设为0
haffTree[i].parent = -1;
haffTree[i].flag = 0;
haffTree[i].leftChild = -1;
haffTree[i].rightChild = -1;
}
//构造哈夫曼树haffTree的n-1个非叶结点
for(i = 0;i < n - 1;i++)
{
//这里假设先进行一次循环,i=0,后面的代码注释方便大家理解
m1=m2=MaxValue;
x1=x2=0;
//找到权值最小和次小的子树,就是找到权值最小的两个结点
for(j = 0;j < n + i;j++) //这里先让i=0;则对于n个叶子结点,按权值最小和次小的顺序连接结点生成哈夫曼树
{
//这里比较每个结点的权值,如果小于上一个结点(已查找的最小权值结点)权值且该结点没有被访问
if(haffTree[j].weight < m1 && haffTree[j].flag == 0)
{
m2 = m1; //令m2为上一个结点(非最小结点的前面的权值)的下标
x2 = x1; //x2为上一个结点(非最小结点的前面的权值)下标
m1 = haffTree[j].weight; //m1记录该结点的权值
x1 = j; //x1为该结点的下标
}
//这里比较每个结点的权值,如果小于非最小结点的前面的结点权值且该结点没有被访问
else if(haffTree[j].weight < m2 && haffTree[j].flag == 0)
{
m2 = haffTree[j].weight; //m2记录该结点的权值
x2 = j; //x2记录该结点的下标
}
//比较完所有的结点后,x1就为最小权值结点的下标,x2就为次小权值结点的下标
}
//将找出的两棵权值最小和次小的子树合并为一棵子树
haffTree[x1].parent = n + i; //x1就为最小权值结点的下标
haffTree[x2].parent = n + i; //x2就为次小权值结点的下标
haffTree[x1].flag = 1; //x1被访问
haffTree[x2].flag = 1; //x2被访问
haffTree[n+i].weight = haffTree[x1].weight + haffTree[x2].weight;
haffTree[n+i].leftChild = x1; //左孩子存储结点x1
haffTree[n+i].rightChild = x2; //右孩子存储结点x2
}
}在main.cpp中编测试一下,改为如下形式:
#include
#include
#include "Haffman.h"
#define MaxValue 10000
using namespace std;
int main(){
cout<<"--------------Huffman文件压缩编码---------------"<>filename;
char ch;
int i;
int n = 256;
int weight[256]={0};
//以二进制流的方式打开文件
FILE* in = fopen(filename,"rb");
if(in == NULL)
{
printf("打开文件失败");
return 0;
}
//扫描文件,获得权重
while(ch = getc(in) != EOF)
{
weight[ch]++;
}
//关闭文件
fclose(in);
//测试哈夫曼树构造函数
HaffNode *myHaffNode = (HaffNode *)malloc(sizeof(HaffNode)*(2*n-1));
if(n >MaxValue)
{
printf("给出的n越界,修改MaxValue");
exit(1);
}
Haffman(weight,n,myHaffNode);
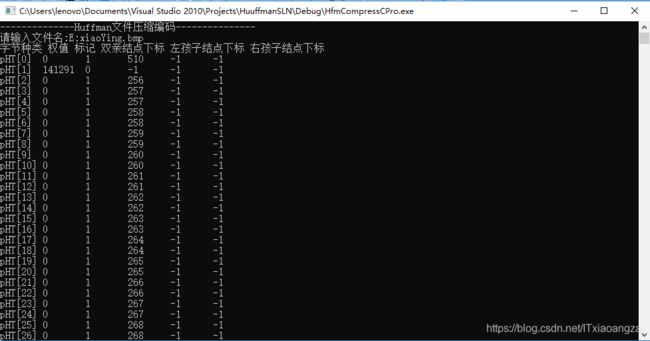
printf("字节种类 权值 标记 双亲结点下标 左孩子结点下标 右孩子结点下标\n");
for(i = 0;i < n;i++)
{
printf("pHT[%d]\t%d\t%d\t%d\t%d\t%d\n",i,myHaffNode[i].weight,myHaffNode[i].flag,myHaffNode[i].parent,myHaffNode[i].leftChild,myHaffNode[i].rightChild);
}
system("pause");
return 0;
} (5)生成哈夫曼编码
按照先序遍历的算法对上面生成的哈夫曼树进行遍历,生成哈夫曼编码。
在Haffman.h文件中创建结构体哈夫曼数组,用于存储编码的起始下表和权值。
在Haffman.cpp文件中创建构造哈夫曼树编码的函数,在Haffman.h文件中声明。
Haffman.h文件
typedef struct
{
int weight; //权值
int flag; //标记
int parent; //双亲结点下标
int leftChild; //左孩子下标
int rightChild; //右孩子下标
}HaffNode;
typedef struct
{
int bit[10000]; //数组
int start; //编码的起始下标
int weight; //字符的权值
}Code;
//创建叶结点个数为n,权值数组为weight的哈夫曼树haffTree
void Haffman(int weight[],int n,HaffNode haffTree[]);
//有n个结点的哈夫曼树haffTree构造哈夫曼编码haffCode
void HaffmanCode(HaffNode haffTree[],int n,Code haffNode[]);Haffman.cpp文件
//有n个结点的哈夫曼树haffTree构造哈夫曼编码haffCode
void HaffmanCode(HaffNode haffTree[],int n,Code haffCode[])
{
Code *cd = (Code *)malloc(sizeof(Code));
int i,j,child,parent;
//求n个叶结点的哈夫曼编码
for(int i = 0;i < n;i++)
{
cd->start = n-1; //不等长编码的最后一位为n-1
cd->weight = haffTree[i].weight; //取得编码对应的权值
child = i;
parent = haffTree[child].weight;
//由叶结点向上直到根节点
while(parent != -1)
{
if(haffTree[parent].leftChild == child) //判断左孩子是否存在
cd->bit[cd->start] = 0;
else //判断右孩子是否存在
cd->bit[cd->start] = 1;
cd->start--;
child = parent;
parent = haffTree[child].parent;
}
for(j = cd->start+1;j < n;j++)
haffCode[j].bit[j] = cd->bit[j];
haffCode[i].start = cd->start + 1;
haffCode[i].weight = cd->weight;
}
}现在在主函数中测试一下:
#include
#include
#include "Haffman.h"
using namespace std;
#define MaxValue 10000
int main(){
cout<<"--------------Huffman文件压缩编码---------------"<>filename;
char ch;
int i,j;
int n = 256;
int weight[256]={0};
//以二进制流的方式打开文件
FILE* in = fopen(filename,"rb");
if(in == NULL)
{
printf("打开文件失败");
fclose(in);
return 0;
}
//扫描文件,获得权重
while(ch = fgetc(in) != EOF)
{
weight[ch]++;
}
//关闭文件
fclose(in);
//显示256个字节出现的次数
cout<<"Byte "<<"Weight"<MaxValue)
{
printf("给出的n越界,修改MaxValue");
exit(1);
}
//测试哈夫曼树构造函数
Haffman(weight,n,myHaffNode);
//测试哈夫曼编码函数
HaffmanCode(myHaffNode,n,myHaffCode);
//输出每个字节叶结点的哈夫曼编码
printf("编码信息为:");
for(i = 0;i < n;i++)
{
//printf("0x%02X ",i);
printf("Weight = %d,Code = ",myHaffCode[i].weight);
for(j = myHaffCode[i].start;j < n;j++)
printf("%d",myHaffCode[i].bit[j]);
printf("\n");
}
system("pause");
return 0;
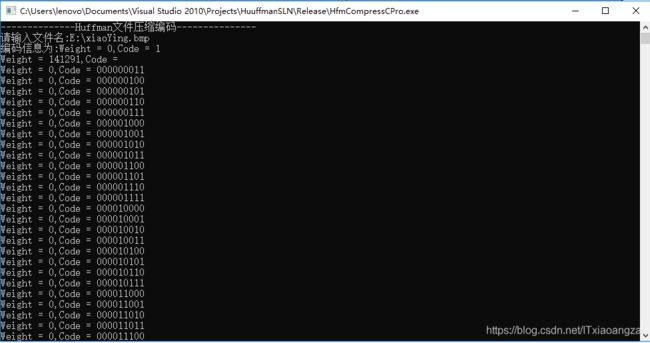
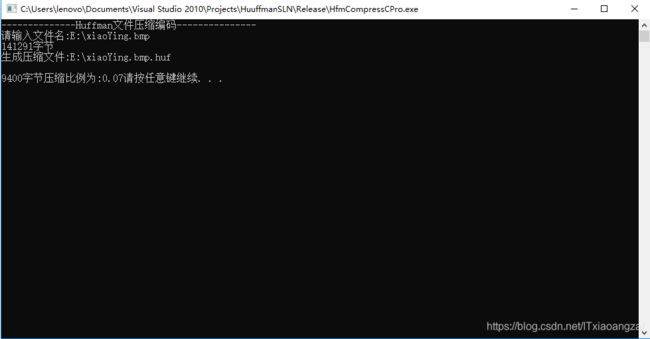
} 运行结果如下:
这里我们发现权值为141291的字节没有显示编码,原因是这个编码个数太长了,在这里显示不出来。
(6)压缩源文件
创建Compress.h和Compress,cpp文件,定义Compress函数用于压缩原文件。
由于编码是以字符数组的形式保存的,重新编码后的数据将是一个很长的字符串,先计算需要的空间,然后把编码按位进行存放到字符数组中,或者直接存放,这里采用直接存放的方式。
int k,ji=0;
int jiShu[1000];
//输出每个字节叶结点的哈夫曼编码
printf("编码信息为:");
for(i = 0;i < n;i++)
{
for(j = myHaffCode[i].start;j < n;j++)
for(k = 0;k < myHaffCode[k].weight+1;k++)
{
printf("%d",myHaffCode[i].bit[j]);
jiShu[ji] = myHaffCode[i].bit[j];
ji++;
}
} 建立一个新文件,文件名为"原文件名字+.huf",将压缩后的数据写入文件。
为了保证压缩后的数据能够被正确解压,必须把相关的解压缩规则写进去,就是把权值信息写入进去,还有文件类型,长度,权值。
在Huffman.h中定义一个文件头结构和InitHead函数声明,在Huffman.cpp中写入函数。
代码如下:
Huffman.h文件
struct HEAD
{
char type[4]; //文件类型
int length; //原文件长度
int weight[256]; //权值数组
}Huffman.cpp文件
//记录文件信息
int initHead(char pFileName[256],HEAD &sHead)
{
int i;
//初始化文件头
strcpy(sHead.type,"bmp");
sHead.length = 0; //原文件长度
for(i = 0;i<256;i++)
{
sHead.weight[i] = 0;
}
//以二进制流的方式打开文件
FILE* in = fopen(pFileName,"rb");
if(in == NULL)
{
printf("打开文件失败");
fclose(in);
return 0;
}
char ch;
//扫描文件,获得权重
while(ch = fgetc(in) != EOF)
{
sHead.weight[ch]++;
sHead.length++;
}
//关闭文件
fclose(in);
in = NULL;
return 0;
}现在我们得到文件的信息和编码,就可以得到压缩后的文件,直接在主函数中写代码:
#include
#include
#include
#include "Haffman.h"
//#include "Compress.h"
using namespace std;
#define MaxValue 10000
int main(){
cout<<"--------------Huffman文件压缩编码---------------"<>filename;
char ch;
int i,j;
int n = 256;
int weight[256]={0};
//以二进制流的方式打开文件
FILE* in = fopen(filename,"rb");
int fn = _fileno(in); /*取得文件指针的底层流式文件号*/
int sz = _filelength(fn);/*根据文件号取得文件大小*/
printf("%d字节\n",sz);
if(in == NULL)
{
printf("打开文件失败");
fclose(in);
return 0;
}
//扫描文件,获得权重
while(ch = fgetc(in) != EOF)
{
weight[ch]++;
}
//关闭文件
fclose(in);
/*
//显示256个字节出现的次数
cout<<"Byte "<<"Weight"<MaxValue)
{
printf("给出的n越界,修改MaxValue");
exit(1);
}
//测试哈夫曼树构造函数
Haffman(weight,n,myHaffNode);
//测试哈夫曼编码函数
HaffmanCode(myHaffNode,n,myHaffCode);
/*
printf("字节种类 权值 标记 双亲结点下标 左孩子结点下标 右孩子结点下标\n");
for(i = 0;i < n;i++)
{
printf("pHT[%d]\t%d\t%d\t%d\t%d\t%d\n",i,myHaffNode[i].weight,myHaffNode[i].flag,myHaffNode[i].parent,myHaffNode[i].leftChild,myHaffNode[i].rightChild);
}
*/
HEAD sHead;
initHead(filename,sHead);
int cc=0;
//生成文件名
char newFileName[256] = {0};
strcpy(newFileName,filename);
strcat(newFileName,".huf");
//以二进制流的方式打开文件
FILE* out = fopen(newFileName,"wb");
//写文件头
//fwrite(&sHead,sizeof(HEAD),1,out);
//int k,ji=0;
//int jiShu[1000];
//输出每个字节叶结点的哈夫曼编码
//printf("编码信息为:");
for(i = 0;i < n;i++)
{
for(j = myHaffCode[i].start;j < n;j++)
{
//printf("%d",myHaffCode[i].bit[j]);
//写压缩后的编码
cc+=sizeof(myHaffCode[i].bit[j]);
}
}
fclose(out);
out = NULL;
cout << "生成压缩文件:" << newFileName <
需要详细代码请私信我:
qq:1657264184
微信:liang71471494741