CodeForces 833B 详细题解(貌似是四边形优化)
833B - The Bakery
B. The Bakery
time limit per test2.5 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard outputSome time ago Slastyona the Sweetmaid decided to open her own bakery! She bought required ingredients and a wonder-oven which can bake several types of cakes, and opened the bakery.
Soon the expenses started to overcome the income, so Slastyona decided to study the sweets market. She learned it’s profitable to pack cakes in boxes, and that the more distinct cake types a box contains (let’s denote this number as the value of the box), the higher price it has.
She needs to change the production technology! The problem is that the oven chooses the cake types on its own and Slastyona can’t affect it. However, she knows the types and order of n cakes the oven is going to bake today. Slastyona has to pack exactly k boxes with cakes today, and she has to put in each box several (at least one) cakes the oven produced one right after another (in other words, she has to put in a box a continuous segment of cakes).
Slastyona wants to maximize the total value of all boxes with cakes. Help her determine this maximum possible total value.
Input
The first line contains two integers n and k (1 ≤ n ≤ 35000, 1 ≤ k ≤ min(n, 50)) – the number of cakes and the number of boxes, respectively.
The second line contains n integers a1, a2, …, an (1 ≤ ai ≤ n) – the types of cakes in the order the oven bakes them.
Output
Print the only integer – the maximum total value of all boxes with cakes.
题目 m个包裹, n个蛋糕,连续划分,每个包裹的价值为这个包裹内蛋糕的种类数,相同数字的蛋糕为同一种蛋糕。求最大总价值。
O(nnnk)
顺序:从左往右,从上往下
for k = 1 to m
for i = k to n
for j = k-1 to i-1
dp[k][i] = max(dp[k][i], dp[k-1][j]+val(j+1, i) );状态数:nk
状态转移复杂度:枚举k O(n), val(j+1, i)的计算O(n)。
总复杂度O(nnnk)
O(nnk)
顺序:从左往右,从上往下
均摊复杂度优化。
val值从(k , i)~( i , i ) 在第三层循环中都会用到,所以,可以在第三层之间先枚举出来,这样就是O(nk*2n)
逆序遍历,记录出现的种类,可以用set。
for k = 1 to m
for i = k to n
for j = i to k
set.insert(a[j])
val[j] = set.size
for j = k-1 to i-1
dp[k][i] = max(dp[k][i], dp[k-1][j]+val[j+1] );O(nk)
类似于隔板法的思想。orz V8老师。
一段k个数字的数列,分割成n份,价值为n份价值总和。这样的问题,自然是在k个数字间插n-1个隔板。
直接用的定理,V8老师说可以反证法证明,但是很长。。。我也还没找。
1. 尽量平均会使价值更大
2. 相同n份,k越大,最后一个隔板越靠后,保持平均嘛。
3. 相同k个,n越大,最后一个隔板越靠后,保持平均嘛。
在这题中,n个蛋糕,分到k个包裹里,满足上面的形式,所以,可以记录转移位置,缩小最后枚举的范围。
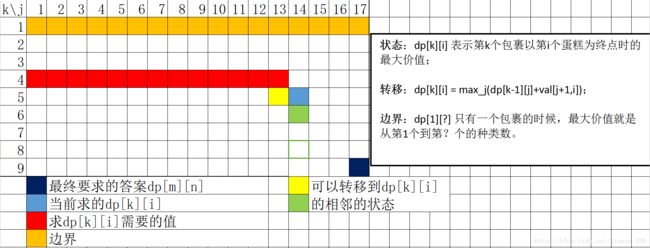
范围,自然一左一右,也就是找转移位置的左边界和右边界。根据上面的定理,[k, i]的左边界不会小于[k,i-1]也不会小于[k-1,i], 右边界不会大于[k+1,i]也不会大于[k,i+1],依次在[k,i]的左、上、下、右,任意选两个。这里我选了左和下,如果想要左和下来推出当前位置,那么,就需要更改计算顺序,以提前求出左和下的值。
顺序:从下往上从左往右
因为以前计算val是O(n)的,n方是过不了的,在这里可以优化为O(1),这样复杂度就为O(nk),优化方法如下:
因为是从下往上从左往右,所以说,就是一列一列的刷表,每递增一列,比如从 i -> i+1,需要的val只是从(?,i )到了( ? , i+1),假设已知到第i列的val,在第i+1列中,当算到一个具体的区间时,我们只要看一下a[i+1](当前位置的值)在不在这个区间内,在的话,不变,不在的话,加一,如何快速知道在不在这个区间呢?可以预处理出于在当前位置的左边,与 当前位置的值 相同的元素的位置在哪。这样,只需要看与它相同的前一个值在不再这个区间内,在的话,就不变,不在的话,就加一,实现了O(1)更新val。
貌似这是平行四边形法则优化?不懂这法则,要有了解的前辈,请不吝赐教。orz。
表述的并不是很清楚,若哪里有疑问,请及时提出。orz V8老师。
可以用滚动数组优化空间,懒得优化了,反正不会爆。
贴代码:
O(nk)的解法
#include 1);
}
if(dp[k][i] < dp[k-1][j]+val[j+1]) {
dp[k][i] = dp[k-1][j]+val[j+1];
tran[k][i] = j; // 记录转移位置
}
}
}
}
printf("%d", dp[m][n]);
return 0;
} O(nnk)的解法
void onnk() { // 复杂度为O(nnk)
memset(dp, 0, sizeof(dp));
for(int k = 1; k <= m; k++) { // 枚举第k个包裹
for(int i = k; i <= n; i++) { // 枚举第k个包裹的结束位置
// 逆序计算val值,均摊复杂度
set<int> mark;
for(int j = i; j >= k; j--) {
mark.insert(a[j]);
val[j] = mark.size();
}
// 边界
if(k == 1) {
dp[k][i] = val[1]; continue;
}
// 状态转移
for(int j = k-1; j < i; j++) {
// dp[k][i] = max(dp[k][i], dp[k-1][j]+val[j+1]);
if(dp[k-1][j]+val[j+1] > dp[k][i]) {
dp[k][i] = max(dp[k][i], dp[k-1][j]+val[j+1]);
tran[k][i] = j;
}
}
}
}
} 打印tran 和dp数组,自己摸索规律,可以理清思路。