动态规化刷题
文章目录
-
- [1143. 最长公共子序列]
- [5. 最长回文子串]
- [647. 回文子串]
- [300. 最长上升子序列]
- [72. 编辑距离]
- Acwing-02-01背包问题
- [416. 分割等和子集]
- [121. 买卖股票的最佳时机]
- [122. 买卖股票的最佳时机 II]
- [123. 买卖股票的最佳时机 III ]
- [309. 最佳买卖股票时机含冷冻期]
- [714. 买卖股票的最佳时机含手续费]
- Acwing-03-完全背包问题
- [322. 零钱兑换]
- [518. 零钱兑换 II]
[1143. 最长公共子序列]
https://leetcode-cn.com/problems/longest-common-subsequence/solution/1143-zui-chang-gong-gong-zi-xu-lie-by-ming-zhi-sha/
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length();
int n = text2.length();
//dp[i][j]代表text1的前i个字符和text2的前j个字符的最长子序列
int[][] dp = new int[m+1][n+1];
for(int i=0;i<m;i++){
for(int j =0;j<n;j++){
if(text1.charAt(i)==text2.charAt(j)){
//因为状态是从0开始的,因此不能写成: dp[i][j] = dp[i-1][j-1]+1;
dp[i+1][j+1] = dp[i][j]+1;
}else {
dp[i+1][j+1] = Math.max(dp[i+1][j],dp[i][j+1]);
}
}
}
return dp[m][n];
}
}
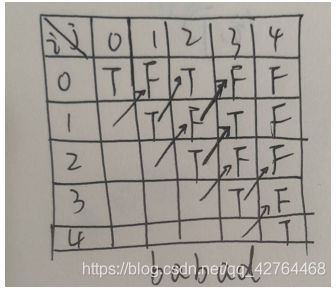
[5. 最长回文子串]
填表的时候,每当计算新 dp 值的时候,都一定会参考「左下角」的 dp 值,即 dp[i + 1][j - 1](i + 1 表示在下边,j - 1 表示在左边)。
边界条件是:表达式 [i + 1, j - 1] 不构成区间,即长度严格小于 2,即 j - 1 - (i + 1) + 1 < 2 ,整理得 j - i < 3。
class Solution {
public String longestPalindrome(String s) {
boolean[][] dp = new boolean[s.length()][s.length()];
int max =0;
String res = "";
for(int j = 0;j<s.length();j++){
for(int i=0;i<=j;i++){
dp[i][j] = s.charAt(i)==s.charAt(j) && (j-i<=2 || dp[i+1][j-1]);
if(dp[i][j] && j-i+1>max){
max = j-i+1;
res = s.substring(i,j+1);
}
}
}
return res;
}
}
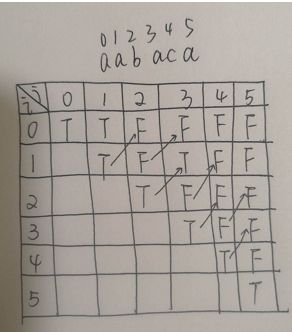
[647. 回文子串]
暴力解法:
class Solution {
public int countSubstrings(String s) {
if(s==null || s.length()==0) return 0;
int count=0;
for(int i=0;i<s.length();i++){
for(int j = i;j<s.length();j++){
if(HuiWen(s,i,j)){
count++;
}
}
}
return count;
}
private boolean HuiWen(String s,int i, int j) {
while (i<j){
if(s.charAt(i)!=s.charAt(j)) return false;
i++;
j--;
}
return true;
}
}
动态规划:
class Solution {
public int countSubstrings(String s) {
if(s.length()==0) return 0;
int count = 0;
boolean[][] dp = new boolean[s.length()][s.length()];
for(int j=0;j<s.length();j++){
for(int i=0;i<=j;j++){
dp[i][j] = (s.charAt(i)==s.charAt(j) && (j-i>=2 || dp[i+1][j-1]));
if(dp[i][j]){
count++;
}
}
}
return count;
}
}
[300. 最长上升子序列]
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length==0) return 0;
//定义dp[i]:前i个字符的最长上升子序列
int[] dp = new int[nums.length];
int res = 0;
for(int i=0;i<nums.length;i++){
dp[i] = 1;
for(int j=0;j<i;j++){
if(nums[i]>nums[j]){
dp[i] = Math.max(dp[j]+1,dp[i]);
}
}
//最终结果应该为dp的最大值:10 9 2 5 6 3 7 21
// 1 1 1 2 3 2 4 5 1
//注意:必须放到for循环外面,求出dp[i]后和res比较取最大值
res = Math.max(res,dp[i]);
}
return res;
}
}
[72. 编辑距离]
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int[][] dp = new int[m+1][n+1];
//因为添加了空字符串,需要时刻注意数组越界的情况
for(int i=0;i<=m;i++){
dp[i][0] = i;
}
for(int i = 0;i<=n;i++){
dp[0][i] = i;
}
for(int i=1;i<=m;i++){
for(int j = 1;j<=n;j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
//对角线位置搬下来
dp[i][j] = dp[i-1][j-1];
}else{
//三者中最小的数加1
dp[i][j] = Math.min(Math.min(dp[i-1][j-1],dp[i][j-1]),dp[i-1][j])+1;
}
}
}
return dp[m][n];
}
}
写法2:
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int[][] dp = new int[m+1][n+1];
for(int i=0;i<=m;i++){
dp[i][0] = i;
}
for(int i = 0;i<=n;i++){
dp[0][i] = i;
}
//当i=0,j=0时对应dp[1][1],dp[0][i]和dp[i][0]填充的是空串
for(int i=0;i<m;i++){
for(int j = 0;j<n;j++){
if(word1.charAt(i)==word2.charAt(j)){
dp[i+1][j+1] = dp[i][j];
}else{
dp[i+1][j+1] = Math.min(Math.min(dp[i][j],dp[i][j+1]),dp[i+1][j])+1;
}
}
}
return dp[m][n];
}
}
Acwing-02-01背包问题
有N件物品和一个容量为V的背包。第i件物品的费用是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
https://www.acwing.com/problem/content/2/
https://www.cnblogs.com/jbelial/articles/2116074.html
注意填表的顺序是从上到下,从左到右填写:
状态转移方程:定义f[i][j]:前i个物品,背包容量j下的最优解
1)当前背包容量不够(j < w[i]),为前i-1个物品最优解:f[i][j] = f[i-1][j]
2)当前背包容量够,判断选与不选第i个物品 选:f[i][j] = f[i-1][j-w[i]] + v[i] 不选:f[i][j] = f[i-1][j]
// 第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
// 接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
// 4 5
// 1 2
// 2 4
// 3 4
// 4 5
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()){
int n = sc.nextInt();
int m = sc.nextInt();
//存放物品的体积(可以多创建一个大小,这样不用考虑后面数组越界的情况)
int[] v = new int[n+1];
//存放物品的价值
int[] w = new int[n+1];
//遍历每一行数据(0的位置不放数据默认为0,数据从1的位置开始存放,这样和dp表就是相同的)
for(int i=1;i<=n;i++){
//这一行的第一个数据是体积
v[i] = sc.nextInt();
//这一行的第二个数据是价值
w[i] = sc.nextInt();
}
//因为我们引入了空行空列
int[][] dp = new int[n+1][m+1];
//base case,这题可以省略,因为数组初始化后本身默认每个元素为0
for(int i=0;i<=n;i++){
dp[i][0] = 0;
}
for(int i=0;i<=m;i++){
dp[0][i] = 0;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(j<v[i]){
dp[i][j] = dp[i-1][j];
}else{
dp[i][j] = Math.max(dp[i-1][j-v[i]]+w[i],dp[i-1][j]);
}
}
}
System.out.println(dp[n][m]);
}
}
}
压缩空间:降低为一维
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()){
int n = sc.nextInt();
int m = sc.nextInt();
//存放物品的体积(可以多创建一个大小,这样不用考虑后面数组越界的情况)
int[] v = new int[n+1];
//存放物品的价值
int[] w = new int[n+1];
//遍历每一行数据(0的位置不放数据默认为0,数据从1的位置开始存放,这样和dp表就是相同的)
for(int i=1;i<=n;i++){
//这一行的第一个数据是体积
v[i] = sc.nextInt();
//这一行的第二个数据是价值
w[i] = sc.nextInt();
}
//因为我们引入了空行空列
int[] dp = new int[m+1];
for(int i=1;i<=n;i++){
for(int j=m;j>=1;j--){
if(j>=v[i]){
dp[j] = Math.max(dp[j-v[i]]+w[i],dp[j]);
}
}
}
System.out.println(dp[m]);
}
}
}
[416. 分割等和子集]
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
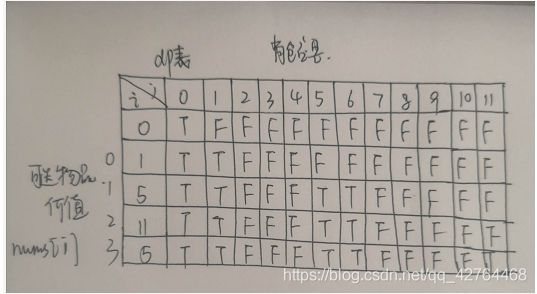
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int i=0;i<nums.length;i++){
sum += nums[i];
}
if(sum%2==1) return false;
int m = sum/2;
boolean[][] dp = new boolean[nums.length+1][m+1];
//如果背包容量为0,那么一定是满的
for(int i=0;i<=nums.length;i++){
dp[i][0] = true;
}
//因为dp数组和nums数组不对应,dp的1代表nums的0,因此遇到nums时,需要减1
for(int i=1;i<=nums.length;i++){
for(int j=1;j<=m;j++){
if(j<nums[i-1]){
dp[i][j] = dp[i-1][j];
}else{
dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];
}
}
}
return dp[nums.length][m];
}
}
[121. 买卖股票的最佳时机]
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
0、暴力算法:
class Solution {
public int maxProfit(int[] prices) {
if(prices==null || prices.length==0) return 0;
int profit = 0;
for(int i=0;i<prices.length;i++){
for(int j=i+1;j<prices.length;j++){
if(prices[i]<prices[j]){
profit = Math.max(profit,prices[j]-prices[i]);
}
}
}
return profit;
}
}
1、动态规划:
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0 || prices==null) return 0;
//dp[i][j]表示第i天是否持有股票,j=0代表不持有(卖出后的不持有,不包括未买入的不持有),j=1代表持有
// dp[i][0]: 卖出后不持有股票
// dp[i][1]: 买入股票
int[][] dp = new int[prices.length][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i=1;i<prices.length;i++){
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
//不能由dp[i-1][0]-prices[i]得到,因为dp[i-1][0]是卖出后的买入,不符合条件
//这个买入只能是第一次买入股票,因为只支持一次买入,不支持卖出后再买入。
dp[i][1] = Math.max(dp[i-1][1],-prices[i]);
}
//不持有这张股票时才能获得最大利润
return dp[prices.length-1][0];
}
}
2、贪心算法:维持一个股票价格的最小值,然后将当前股票价格额最小值做差值求利润
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0 || prices==null) return 0;
int minPrice = prices[0];
int profit = 0;
//如果你最多只允许完成一笔交易(即买入和卖出一支股票一次)
//在股票最低价格的时候买入,利润最高的时候卖出
for(int i=1;i<prices.length;i++){
if(prices[i]<minPrice){
minPrice = prices[i];
}
profit = Math.max(profit,prices[i]-minPrice);
}
return profit;
}
}
[122. 买卖股票的最佳时机 II]
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
1、动态规划:注意这一题和上一题的区别,支持多次买入和多次卖出
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0 || prices==null) return 0;
//dp[i][j]: 第i天是否持有股票,0表示不持有,1表示持有
int[][] dp = new int[prices.length][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i=1;i<prices.length;i++){
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
//不同点在于这儿,持有股票可以是因为上次卖出后又买入可以多次买入卖出
//所以支持多次买入和卖出可以直接写成dp[i-1][0]-prices[i]
//也可以分开写成:第一次买入后持有,卖出后买入持有,上一次就持有
//dp[i][1] = Math.max((Math.max(dp[i-1][1],dp[i-1][0]-prices[i])),-prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
return dp[prices.length-1][0];
}
}
2、贪心算法:
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0) return 0;
int profit = 0;
int price = prices[0];
// res = (prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])
// = prices[3] - prices[0]
// 你可以尽可能地完成更多的交易(多次买卖一支股票)。今天卖出后可以再买入
for(int i=1;i<prices.length;i++){
int tmp = prices[i]-prices[i-1];
if(tmp>0){
profit = profit+tmp;
}
}
return profit;
}
}
[123. 买卖股票的最佳时机 III ]
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0 || prices==null) return 0;
// dp[i][j]:在第i天持股状态为j时的最大利润
// j=0:代表第一次买入股票
// j=1:代表第一次卖出股票
// j=2:代表第二次买入股票
// j=4:代表第二次卖出股票
int[][] dp = new int[prices.length][4];
dp[0][0] = -prices[0];
//第二次买入股票时,只有在之前的状态有被赋值的时候,才可能有当前状态
//因此需要赋值一个不能能的数,当到达该状态时会更新
for (int i = 0; i < prices.length; i++) {
dp[i][2] = Integer.MIN_VALUE;
}
for(int i=1;i<prices.length;i++){
dp[i][0] = Math.max(dp[i-1][0],-prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]-prices[i]);
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]+prices[i]);
}
//当卖出股票的时候会获得最大利润
return Math.max(dp[prices.length-1][1],dp[prices.length-1][3]);
}
}
[309. 最佳买卖股票时机含冷冻期]
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0) return 0;
//dp[i][j]:在第i天持股状态为j时的最大利润
//j=0:持股:第一次买入持股,卖出后又买入持股(支持多次买入和卖出),上一次就持股
//j=1:冷冻:持股卖出后变成冷冻
//j=2:不持股:冷冻时不持股,上一个状态就不持股(注意:持股卖出后不会变成不持股)
int[][] dp = new int[prices.length][3];
dp[0][0] = -prices[0];
for(int i=1;i<prices.length;i++){
dp[i][0] = Math.max(Math.max(-prices[i],dp[i-1][2]-prices[i]),dp[i-1][0]);
dp[i][1] = dp[i-1][0]+prices[i];
dp[i][2] = Math.max(dp[i-1][1],dp[i-1][2]);
}
return Math.max(dp[prices.length-1][1],dp[prices.length-1][2]);
}
}
[714. 买卖股票的最佳时机含手续费]
class Solution {
public int maxProfit(int[] prices, int fee) {
if(prices.length==0) return 0;
//dp[i][j]:在第i天持股状态为j时的最大收益(这个收益需要在一笔交易时减去手续费)
//假如我们规定在卖出时扣除手续费
// j=0(不持股):上一天就不持股,上一天持股卖出后不持股
// j=1(持股):上一天不持股买入后持股:第一次买入后持股和卖出后买入持股,上一天就持股
int[][] dp = new int[prices.length][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i=1;i<prices.length;i++){
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]-fee);
dp[i][1] = Math.max(Math.max(dp[i-1][0]-prices[i],-prices[i]),dp[i-1][1]);
}
return dp[prices.length-1][0];
}
}
Acwing-03-完全背包问题
/**
* 第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
*
* 接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
*
* 4 5
* 1 2
* 2 4
* 3 4
* 4 5
*/
public class Main{
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()){
//物品的数量
int n = scanner.nextInt();
//背包的体积
int m = scanner.nextInt();
//每件物品的体积
int[] v = new int[n+1];
//每件物品的价值
int[] w = new int[n+1];
for(int i=1;i<=n;i++){
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
//前i个物品恰好放入容量为j的背包时获取到的最大价值
int[][] dp = new int[n+1][m+1];
/**
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=0;k*v[i]<=j;k++){
if(j
dp[i][j] = Math.max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
}
}
}
}
**/
//优化复杂度:优化后和0-1别抱相同,但是0-1背包是逆序,完全背包是倒叙
//下面这个公式推导得出的
int[] dp = new int[m+1];
for(int i=1;i<=n;i++){
for(int j=v[i];j<=m;j++){
dp[j] = Math.max(dp[j],dp[j-v[i]]+w[i]);
}
}
System.out.println(dp[n][m]);
}
}
}
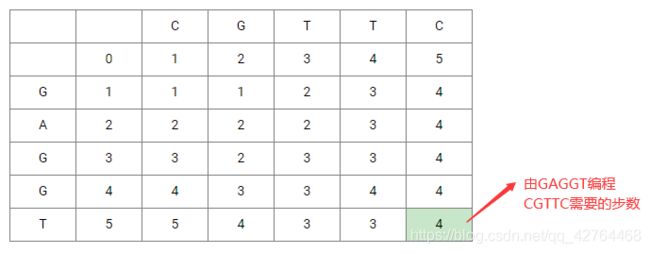
[322. 零钱兑换]
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
class Solution {
public int coinChange(int[] coins, int amount) {
if(coins.length==0 || coins==null) return 0;
int[] dp = new int[amount+1];
dp[0] = 0;
for(int i=1;i<=amount;i++){
dp[i] = amount+1;
for(int j=0;j<coins.length;j++){
if(i>=coins[j]){
dp[i] = Math.min(dp[i-coins[j]]+1,dp[i]);
}
}
}
return dp[amount] == amount+1 ? -1 :dp[amount];
}
}
[518. 零钱兑换 II]
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
最原始的安全背包做法:
class Solution {
public int change(int amount, int[] coins) {
//dp[i][j]:前i个硬币组成金额为j的组合数
int[][] dp = new int[coins.length + 1][amount + 1];
dp[0][0] = 1;
for (int i = 1; i <= coins.length; i++) {
for (int j = 0; j <= amount; j++) {
for (int k=0; k*coins[i-1]<=j; k++) {
//完全背包问题:选择0个、1个、2个、....k个
dp[i][j] += dp[i-1][j-k*coins[i-1]];
}
}
}
return dp[coins.length][amount];
}
}
优化时间和空间复杂度:
状态定义:
dp[i][j] 使用前i种硬币计算j分的表示法种数
推导状态转移方程:
dp[i][j] = dp[i-1][j] + dp[i-1][j-coins[i]] + dp[i-1][j-2*coins[i]] + ... dp[i-1][j-k*coins[i]] (其中,j >= k*coins[i]) - 式1
把j替换成j-coins[i]:
dp[i][j-coins[i]] = dp[i-1][j-coins[i]] + dp[i-1][j-2*coins[i]] + ... dp[i-1][j-k*coins[i]] -式2
(注意dp[i-1][j-(k+1)*coins[i]]取不到,因为不满足k是满足j >= k*coins[i])的最大值,舍去)
式2代入式1:
dp[i][j] - dp[i][j-coins[i]] = dp[i-1][j]
最终得到:
dp[i][j] = dp[i][j-coins[i]] + dp[i-1][j]
优化时间和空间复杂度之后:
class Solution {
public int change(int amount, int[] coins) {
//dp[i][j]:前i个硬币组成金额为j的组合数
int[] dp = new int[amount + 1];
//没有时候,不选任何,可以组成金额为0,只有这么一种组合,dp[0]等价于dp[0][0]
dp[0] = 1;
for (int i = 1; i <= coins.length; i++) {
for (int j = coins[i-1]; j <= amount; j++) {
dp[j] = dp[j]+dp[j-coins[i-1]];
}
}
return dp[amount];
}
}