【数据结构与算法】->算法->分治算法->MapReduce的基本思想
分治算法
-
- Ⅰ 前言
- Ⅱ 分治算法的理解
- Ⅲ 分治算法的应用
- Ⅳ 分治思想在海量数据处理中的应用
- Ⅴ MapReduce 的基本思想
Ⅰ 前言
MapReduce 是 Google 大数据处理的三驾马车之一,另外两个是 GFS 和 Bigtable,它在倒排索引、PageRank 计算、网页分析等搜索引擎相关的技术中都有大量的应用。
尽管开发一个 MapReduce 看起来很高深,和我们遥不可及,但是万变不离其宗,它的本质就是我们这篇文章要讲的这种算法思想——分治算法。
Ⅱ 分治算法的理解
分治算法(divide and conquer) 的核心思想其实就是四个字:分而治之,也就是将原问题划分成 n 个规模较小,并且结构与原问题相似的子问题,递归地解决这些子问题 ,然后再合并其结果,就得到原问题的解。
这个定义看起来很像是递归的定义,其实,总结地说就是:分治算法是一种处理问题的思想,递归是一种编程技巧。 实际上,分治算法一般都比较适合用递归来实现。分治算法一般都比较适合用递归来实现。
在分治算法的递归实现中,每一层递归都会涉及这样三个操作:
- 分解: 将原问题分解成一系列子问题;
- 解决: 递归地求解各个子问题,若子问题足够小,则直接求解;
- 合并: 将子问题的结果合并成原问题。
分治算法能解决的问题,一般需要满足下面这几个条件:
- 原问题分解成的小问题具有相同的模式;
- 原问题分解成的子问题可以独立求解,子问题之间没有相关性,这一点是分治算法跟动态规划的明显区别。
- 具有分解终止条件,也就是说,当问题足够小时,可以直接求解;
- 可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果。
Ⅲ 分治算法的应用
理解分治算法的原理并不难,但是要想灵活应用并不容易。所以接下来,我们就来看看分治算法在解决排序时涉及到的一个问题。
在排序中,有一个逆序度、有序度的概念,我在我的一篇文章中讲过。
【数据结构与算法】->算法->排序(一)->冒泡排序&插入排序&选择排序
这里我直接将那篇文章里的概念搬过来。
有序度是数组中具有有序关系的元素对的个数。有序元素对用数学表达式表示就是这样:
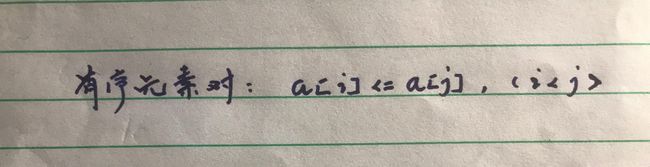

同理,对于一个倒序排列的数组,比如 6, 5, 4, 3, 2, 1,有序度就是 0;对于一个完全有序的数组,比如 1, 2, 3, 4, 5, 6,有序度就是 n * (n - 1) / 2,也就是15。我们把这种完全有序的数组的有序度叫作 满有序度。
逆序度的定义正好跟有序度相反,(默认从小到大为有序)。
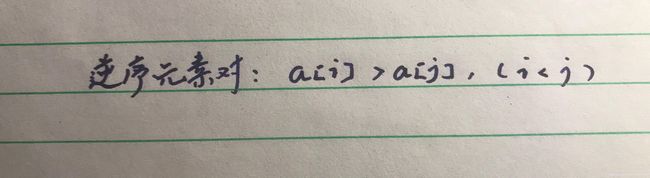
假设我们有 n 个数据,我们期望数从小到大排列,那完全有序的数据的有序度就是 n(n-1)/2,逆序度等于 0;相反,倒序排列的数据的有序度就是 0;逆序度是 n(n-1)/2。除了这两种极端情况外,我们通过计算有序或者逆序对的个数,来表示数据的有序度或逆序度。
现在的问题是,如何变成求出一组数据的有序对个数或者逆序度个数呢?因为有序对个数和逆序对个数的求解方法是类似的,所以我们可以只思考逆序对个数的求解方法。
最笨的方法是,拿每个数字跟它后面的数字比较,看有几个比它小的。我们把比它小的数字个数记作 k,通过这样的方式,把每个数字都考察一遍之后,然后对每个数字对应的 k 值求和,最后得到的总和就是逆序对的个数。不过这样的操作的时间复杂度是 O(n2)。那有没有更加高效的处理方法呢?
我们可以用分治算法的思想来考虑。套用分治的思想来求数组 A 的逆序对个数,我们可以将数组分成前后两半 A1 和 A2,分别计算 A1 与 A2 的逆序对个数 K1 和 K2,然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1 + K2 + K3。
我们前面说了,使用分治算法其中一个要求是,子问题合并的代价不能太大,否则就起不了降低时间复杂度的效果了。那回到这个问题,我们要怎么快速计算出两个子问题 A1 与 A2 之间的逆序对个数呢?
这里就要借助归并排序算法了。如果你对归并排序还不清楚,可以看我下面这篇文章
【数据结构与算法】->算法->排序(二)->归并排序&快速排序
归并排序中有一个非常关键的操作,就是将两个有序的小数组,合并成一个有序的数组。实际上,在合并的过程中,我们就可以计算这两个小数组的逆序对个数了。每次合并操作,我们都计算逆序对个数,把这些计算出来的逆序对个数求和,就是这个数组的逆序对个数了。
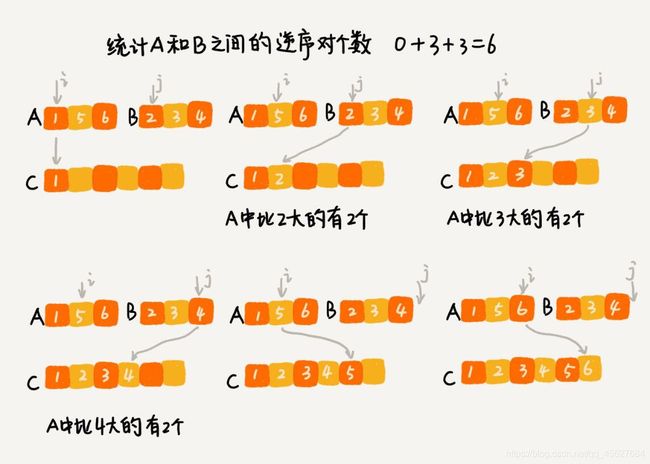
比如我们第一次,先比较的是 A 数组中的 1 和 B 数组中的 2,发现1 比 2 小,将 1放入 C 中,将 i 向后移,j 不动。第二次比较,这时候 我们先看 A 数组中有几个元素比 B 数组中下标为 j 的元素大,发现是 2 个,我们做一个记录,然后比较两个元素大小做排序。以此类推。
实现的代码如下,大家可以对照着讲解做一个参考
package com.tyz.about_sort.core;
/**
* 分治算法,借助归并排序计算数组的逆序度
* @author Tong
*/
public class MergeSortCounting {
private int num;
public MergeSortCounting() {
}
/**
* 利用归并排序统计数组的逆序度
* @param arr 数组
* @return 数组的逆序度
*/
public int count(int[] arr) {
num = 0;
mergeSortCounting(arr, 0, arr.length - 1);
return num;
}
private void mergeSortCounting(int[] arr, int start, int end) {
if (start >= end) {
return;
}
int middle = (start + end) / 2;
mergeSortCounting(arr, start, middle);
mergeSortCounting(arr, middle + 1, end);
mergeSort(arr, start, middle, end);
}
private void mergeSort(int[] arr, int start, int middle, int end) {
int i = start;
int j = middle + 1;
int k = 0;
int[] tmp = new int[middle-start+1];
while (i <= middle && j <= end) {
if (arr[i] <= arr[j]) {
tmp[k++] = arr[i++];
} else {
num += (middle - i + 1); //统计start~middle之间,比arr[j]大的元素个数
}
}
//处理剩下的元素
while (i <= middle) {
tmp[k++] = arr[i++];
}
while (j <= end) {
tmp[k++] = arr[j++];
}
for (i = 0; i <= end-middle; i++) {
arr[start+i] = tmp[i]; //将排序好的元素拷贝到原数组中
}
}
}
关于分治算法,还有两道很经典的题,大家有兴趣可以看看,在之后我会把这两道题的源码补充上来。
- 二维平面上有 n 个点,如何快速计算出两个距离最近的点对?
- 有两个 n*n 的矩阵 A,B,如何快速求解这两个矩阵的乘积 C = A * B?
Ⅳ 分治思想在海量数据处理中的应用
分治算法思想的应用是非常广泛的,并不仅限于指导编程和算法设计。它还经常用在海量数据处理的场景中。一般的基础的数据结构和算法,都是基于内存存储和单机处理。但是,如果要处理的数据量非常大,没法一次性放到内存中,这个时候,这些数据结构和算法就无法工作了。
比如,给 10GB 的订单文件按照金额排序这样一个需求,看似是一个很简单的排序问题,但是因为数据量大,有 10GB,而我们的机器的内存可能只有 2、3GB,无法一次性加载到内存,也就无法通过单纯地使用快排、归并等基础算法来解决了。
要解决这种数据量大到内存装不下的问题,我们就可以利用分治的思想,将海量的数据集合根据某种方法,划分为几个小的数据集合,每个小的数据集合单独加载到内存中来解决,然后再将小数据集合合并成大数据集合。实际上,利用这种分治的处理思想,不仅能克服内存的限制,还能利用多线程或者多机处理,加快处理的速度。
比如这个订单排序的例子,给 10GB 的订单排序,我们就可以先扫描一遍订单,将 10GB 划分成几个金额区间。比如订单金额为 1 到 100 元的放到一个小文件,101 到 200 之间的放到一个小文件,以此类推,这样每个小文件都可以单独加载到内存排序,最后将这些有序的小文件合并,就是最终有序的 10GB 订单数据了。
如果订单数据存储在类似 GFS 这样的分布式系统上,当 10GB 的订单被划分成多个小文件的时候,每个文件可以并行加载到多台机器上处理,最后再将结果合并到一起,这样并行处理的速度也加快了很多。不过,这里还有一个点要注意,就是数据的存储与计算所在的机器是同一个或者在网络中靠得很近(比如一个局域网内,数据存取速度很快),否则就会因为数据访问的速度,导致整个处理过程不但不会变快,反而有可能变慢。
Ⅴ MapReduce 的基本思想
我们前面举的例子,数据有 10GB 大小,可能你觉得没什么,那如果我们要处理的数据是 1T、10T、100T 这么多呢?那一台机器处理的效率肯定是非常低了。而对于谷歌搜索引擎来说,网页爬取、清洗、分析、分词、计算权重、倒排索引等等各个环节中,都会面对如此海量的数据(比如网页)。所以,利用集群并行处理显然是大势所趋。
一台机器过于低效,那我们把任务拆分到多台机器上来处理,如果拆分之后的小任务之间互不干扰,独立计算,最后再将结果合并,这不就是分治思想吗?
实际上,MapReduce 框架只是一个任务调度器,底层依赖 GFS 来存储数据,依赖 Borg 管理机器。它从 GFS 中拿数据,交给 Borg 中的机器执行,并且时刻监控机器执行的进度,一旦出现机器宕机、进度卡壳等,就重新从 Borg 中调度一台机器执行。
尽管 MapReduce 的模型非常简单,但是在 Google 内部应用非常广泛,它除了可以用来处理这种数据与数据之间存在关系的任务,比如 MapReduce 的经典例子,统计文件中单词出现的频率,除此之外,它还可以用来处理数据与数据之间没有关系的任务,比如对网页分析、分词等,每个网页可以独立的分析、分词,而这两个网页之间没有关系。网页几十亿、上百亿,如果单机处理,效率低下,我们就可以利用 MapReduce 提供的高可靠、高性能、高容错的并行计算框架,并行地处理这几十亿、上百亿的网页。
另,这篇文章的主要内容来源于极客时间王争的《数据结构与算法之美》。