借助BM算法思想来理解KMP算法思想

上一章节我们说了BM算法，可以说，BM算法是一种很复杂的算法，高性能的同时也带有着很麻烦的处理，需要考虑到诸多因素，用代码来实现也是很复杂的。不过BM算法似乎也不是被我们所常用的算法，很多时候，我们提到字符串匹配，最先想到的就是KMP算法。

尽管在实际的开发中，我们不太可能亲手去实现KMP算法。但是，学习这个算法的思想，作为让你开拓眼界、锻炼下逻辑思维，也是极好的，所以我觉得有必要说一说，但也很难。

实际上KMP算法跟BM算法的本质是一样的。上次我们说了好后缀和坏字符规则，今天就来看一下，如何借助BM算法的讲解思路，更好的理解KMP算法 。

KMP算法基本思想

KMP算法的核心思想，和上一节讲的BM算法非常相近。我们假设主串是a，模式串是b。在模式串与主串匹配的过程中，当遇到不可匹配的字符的时候，我们希望找到一些规律，可以将模式串往后多滑动几位，跳过那些肯定不会匹配的情况。

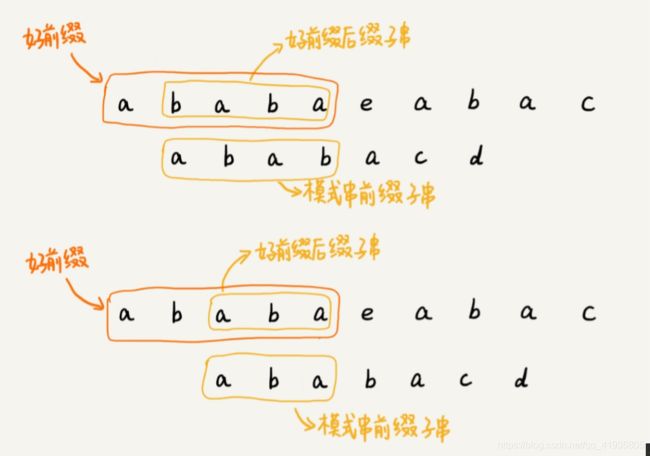
我们可以类比一下好后缀和坏字符，在模式串和主串匹配的过程中，把能匹配的那个字符仍然叫做坏字符，把已经匹配的那段字符串叫做好后缀。

当遇到坏字符的时候，我们就要把模式串往后滑动，在滑动的过程中，只要模式串和好前缀有上下重合，前面几个字符的比较，就相当于拿好前缀的后缀子串，跟模式串的前缀子串在比较。

这样是否能在比较的过程中更加高效了呢？可以不用一个字符一个字符比较了吗？

KMP算法就是在试图寻找一种规律：在模式串和主串匹配的过程中，当遇到坏字符后，对于已经比对过的好前缀，能否找到一种规律，将模式串一次性滑动很多位。

我们只需要那好前缀本身，在他的后缀子串中，查找最长的那个可以跟好前缀的前缀子串匹配的。假设最长的可匹配的那部分前缀子串是{v}，长度是k。我们把模式串一次性往后滑动j-k位，相当于，每次遇到坏字符的时候，我们把j更新为k，i不变，然后继续比较。

为了表述起来方便，我把好前缀的所有子串中，最长可匹配前缀子串的那个后缀子串，叫做最长可匹配后缀子串，对应的前缀子串，叫做最长可匹配前缀子串。

如何求好前缀的最长可匹配前缀 和 后缀子串 呢？我发现，这个问题其实不涉及主串，只需要通过模式串本身就能求解。所以，就可以考虑一下是不是能预先处理好之后再来拿来与主串去对比。

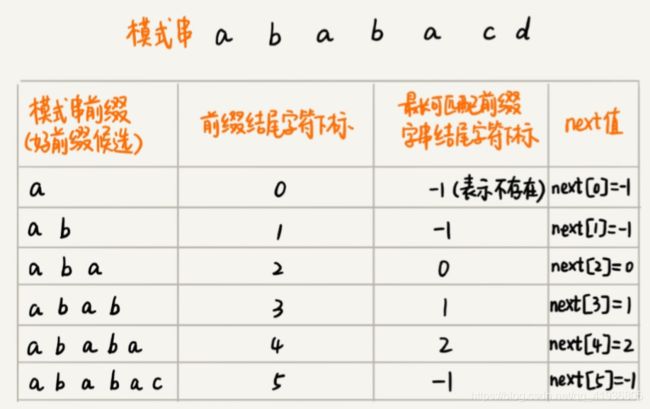
类似BM算法中的bc，suffix，prefix数组，KMP算法也可以提前构建一个数组，用来存储模式串中每个前缀（这些前缀都有可能是好前缀）的最长可匹配前缀子串的结尾字符下标。我们把这个数组定义为next数组，很多书中还给这个数组起了一个名字，叫做失效函数(failure function)。

数组的下标是每个前缀结尾字符下标，数组的值是这个前缀的最长可以匹配的前缀子串的结尾字符下标。这句话有点拗口，可以看下图：

有个next数组，就可以很容易实现KMP算法了。先假设next数组已经计算好了，然后可以看看KMP算法的框架代码。

//b表示模式串，a表示模式串的长度
    private static int[] getNexts(char[] b, int m) {
     
        int[] next = new int[m];
        next[0] = -1;
        int k = -1;
        for (int i = 1; i < m; i++) {
     
            while (k != -1 && b[k + 1] != b[i]) {
     
                k = next[k];
            }
            if (b[k + 1] == b[i]) {
     
                ++k;
            }
            next[i] = k;
        }
        return next;
    }

KMP 算法复杂度分析

KMP算法的原理和实现就算是说完了，现在来分析一下KMP的算法的时间、空间复杂度是多少？

空间复杂度很容易分析，KMP算法只需要一个额外的next数组，数组的大小跟模式串相同。所以空间复杂度O(m)，m表示模式串的长度。

KMP算法包含两部分，第一部分是构建next数组，第二部分才是借助next数组匹配。所以，关于时间复杂度，我们要分别从这两部分来分析。

• 第一部分的时间复杂度

计算next数组的代码中，第一层for循环中i从1到m-1，也就是说，内部的代码被执行了m-1次。for循环内部代码有一个while循环，如果我们能知道每次for循环、while循环平均执行的次数，假设是k，那时间复杂度就是O(k*m)。但是，while循环执行的次数不怎么好统计，所以我们放弃这种分析方法。
、
我们可以找一些参照变量，i和k。i从1开始一直增加到m，而k并不是每次for循环都会增加，所以，k累积增 加的值肯定小于m。而while循环里k=next[k]，实际上是在减小k的值，k累积都没有增加超过m，所以while 循环里面k=next[k]总的执行次数也不可能超过m。因此，next数组计算的时间复杂度是O(m)。

我们再来分析第二部分的时间复杂度。分析的方法是类似的。

i从0循环增长到n-1，j的增长量不可能超过i，所以肯定小于n。而while循环中的那条语句j=next[j-1]+1，不 会让j增长的，那有没有可能让j不变呢？也没有可能。因为next[j-1]的值肯定小于j-1，所以while循环中的这 条语句实际上也是在让j的值减少。而j总共增长的量都不会超过n，那减少的量也不可能超过n，所以while 循环中的这条语句总的执行次数也不会超过n，所以这部分的时间复杂度是O(n)。

所以，综合两部分的时间复杂度，KMP算法的时间复杂度就是O(m+n)。