八皇后问题
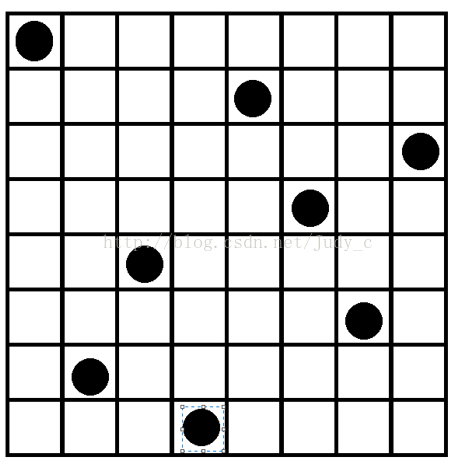
八皇后问题是经典的递归问题,题目的要求是这样的:在国际象棋中,皇后是最强大的棋子,它可以吃掉任何跟自己同行,同列,或同一斜线上的棋子。求如何排列皇后,使得每一行都有一个皇后又让每一个皇后都不能互相攻击,给出所有的排列可能。
首先我们做一些基础工作:
1、 用一个二维数组来表示棋盘,“0”代表该位置无棋子,“1”代表有皇后;
2、 我们要能够判断一个位置是否能够放置皇后(即检测该点同行,同列或同一斜线上有无皇后);
3、 要能够输出一个棋盘;
根据以上的要求,我们先编写进行非核心段却又必不可少的代码:
(1)判断一个位置能否放置皇后的代码:
int isSafe(int (* chess)[EIGHT], int row, int col) {
int i;
int j;
for (i = row - 1; i >= 0; i--) {
if (chess[i][col] == 1) {
return 0;
}
}
for (i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (chess[i][j] == 1) {
return 0;
}
}
for (i = row - 1, j = col + 1; i >= 0 && j < EIGHT; i--, j++) {
if (chess[i][j] == 1) {
return 0;
}
}
return 1;
}
(2)输出棋盘
void showChess(int(*chess)[EIGHT]) {
int i;
int j;
printf("\n");
for (i = 0; i < EIGHT; i++) {
for (j = 0; j < EIGHT; j++) {
printf("%d", chess[i][j]);
}
printf("\n");
}
}
接下来我们就开始着手解决如何找出所有可能性的八皇后排列问题:
八皇后问题最关键的问题是如何能够遍历所有的情况,国际象棋的棋盘有八行八列,也就是说要尝试8^8种情况,如果用循环实现的话,效果可想而知。
我们既然想要用递归的方式实现八皇后问题,就要找到每一次函数调用的普适性规律,只有保证每一步都是相同的操作,才能够使用递归调用函数。通过观察我们发现,要解决八皇后问题,每一行都应该放置且只放置一个皇后,而每一个位置都应该尝试去放一个皇后,再进行判断这样放置是否合理。如果一个位置可以放置皇后了,我们又要看下一行能否放置皇后且不冲突,当判断完该行某一位置能够放置皇后了,就应该继续尝试下一行,当之后的所有行都尝试完毕了,再进行该行的下一个点的尝试。
总结以上的内容可以得出这样的结论:
1、 处理八皇后问题应该是以行为单位逐行测试的;
2、 每一行的处理都应该是相同的;
3、 每一个位置的检测都应该是:放置一个皇后-判断是否可以放置皇后-进行下一行的测试,看当前的排列方式能否构成一种解决方案;
4、 当测试到第八行的时候,如果存在可以放置的皇后,则输出当前的棋盘(当前函数的结束条件,说明找到了一种解决方案,可以进行下一种解决方案的尝试了);
5、 当某一行测试到第八个位置的时候,依然没有位置可以放置皇后,则放回上一行进行下一个点的尝试(这一点在实际编程中不用考虑,因为根据递归调用的性质,每一行的每一个位置的测试都包括该行的之后所有行所有的位置的测试,测试完一整行就代表这一行以下的所有行都已经测试完毕),当然应该返回上一层进行下一个点的测试。
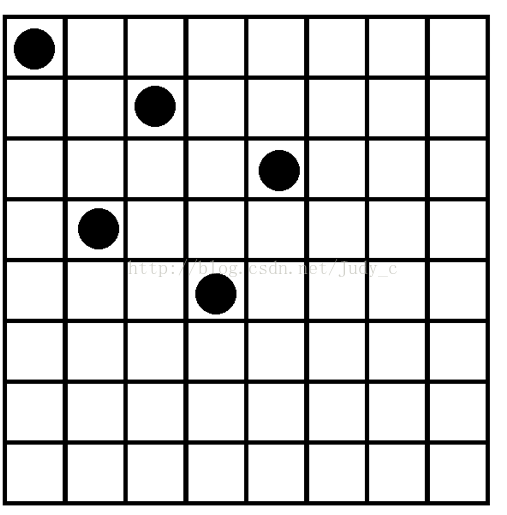
例如该图的第六行所有位置都无法放置皇后,自然第七八行也没必要测试了,因此对于这种排列情况的测试已经完毕,需要做的就是改变第五行的皇后的位置继续测试。
有了以上的分析我们就可以编写八皇后问题的相关代码了:
void eightQueen(int(*chess)[EIGHT], int row) {
int col;
if (row >= EIGHT) {
showChess(chess);
return;
}
for (col = 0; col < EIGHT; col++) {
if (isSafe(chess, row, col)) {
chess[row][col] = 1;
eightQueen(chess, row + 1);
chess[row][col] = 0;
}
}
}
通过以上的比喻,可以更加清晰地看出八皇后问题的本质,以及递归函数在编写时简单却又不容易想到的编程思路。