显式积分，隐式积分和弹簧质点系统（详细公式推导和太极源码）

本人初学者，零基础入门（大二数学基础），因此本教程还算比较舒适，但是也免不了有错误，还请批评指正。

---

数值积分

数值积分，是用于求定积分的近似值的一种方法。在数学分析中，有很多计算给定函数的定积分是不可行的，而数值积分是利用黎曼积分等数学定义，用数值逼近的方法近似计算给定的定积分值。借助计算机和编程，数值积分可以快速而有效地计算复杂的积分。

---

欧拉方法

欧拉方法是一种数值积分方法，又称为欧拉折线法，是用折线来逼近曲线的一种方法。

例如$\frac{dy}{dx}=f(x,y)$，可以转化为$y_{n+1}-y_n=f(x_n,y_n)h$，其中h则为折线的步长。

由泰勒公式$y(x+h)=y(x)+y^{{}^{\prime }}(x)h+o(h)$，可以看出欧拉公式实际上是泰勒公式的离散形式。很显然，h越小，欧拉方法的结果越精确，h越大，结果越不精确。

但是h较大时，除了不精确之外，还会导致使用欧拉方法得到的值不收敛，即不稳定。

欧拉方法分为显式积分和隐式积分两种形式，其中显式积分条件稳定，隐式积分无条件稳定：

---

弹簧质点系统

在清楚了数值积分的解决方法之后，我们使用它来解决一个最简单的物理模拟问题——弹簧质点系统。

弹簧质点系统中主要有弹力和阻力。


总结弹力和阻力的计算公式如下：

$$\{\begin{array}{c}f(x_a{)}_s=-k_s\frac{x_a-x_b}{||x_a-x_b||}(||x_a-x_b||-l)\\ \\ f(x_a{)}_d=-k_d\frac{x_a-x_b}{||x_a-x_b||}(x_a^{{}^{\prime }}-x_b^{{}^{\prime }})\cdot \frac{x_a-x_b}{||x_a-x_b||}\end{array}$$

显式方法

$$\{\begin{array}{c}{f}_t={\sum }_{b=0}^{n}f(x_a{)}_s+{\sum }_{b=0}^{n}f(x_a{)}_d\\ \\ v_{t+dt}=v_t+dt\ast \frac{f_t}{m}\\ \\ x_{t+dt}=x_t+dt\ast v_t\end{array}$$

显式方法直接实现即可。

半隐式方法

$$\{\begin{array}{c}{v}_{t+dt}=v_t+dt\ast \frac{f_t}{m}\\ \\ x_{t+dt}=x_t+dt\ast v_{t+dt}\end{array}$$

可以直接实现，求速度时使用显式，求位移时使用隐式。

隐式方法

$$\{\begin{array}{c}{v}_{t+dt}=v_t+dt\ast \frac{f_{t+dt}}{m}\\ \\ x_{t+dt}=x_t+dt\ast v_{t+dt}\end{array}$$

隐式方法需要进行特殊的推导。

由泰勒公式的一阶展开，可以得到f的近似：

$f_{t+dt}=f_t+\frac{\partial f}{\partial x}△x+\frac{\partial f}{\partial v}△v$

代入上式，可以求得△v的表示形式为：

$△v=v_{t+dt}-v_t=dt\ast \frac{f_{t+dt}}{m}$

$△v=\frac{dt}{m}\ast (f_t+\frac{\partial f}{\partial x}△x+\frac{\partial f}{\partial v}△v)$

将△x也表示为△v的式子：

$△x=x_{t+dt}-x_t=dt\ast v_{t+dt}=dt\ast (v_t+△v)$

代入上式，消去△x：

$△v=\frac{dt}{m}\ast (f_t+dt\ast \frac{\partial f}{\partial x}(v_t+△v)+\frac{\partial f}{\partial v}△v)$

展开括号：

$△v=\frac{dt}{m}\ast f_t+\frac{d{t}^2}{m}\frac{\partial f}{\partial x}{v}_t+\frac{d{t}^2}{m}\frac{\partial f}{\partial x}△v+\frac{dt}{m}\frac{\partial f}{\partial v}△v$

移项：

$△v-\frac{d{t}^2}{m}\frac{\partial f}{\partial x}△v-\frac{dt}{m}\frac{\partial f}{\partial v}△v=\frac{dt}{m}\ast f_t+\frac{d{t}^2}{m}\frac{\partial f}{\partial x}{v}_t$

整理：

$(1-\frac{d{t}^2}{m}\frac{\partial f}{\partial x}-\frac{dt}{m}\frac{\partial f}{\partial v})△v=\frac{dt}{m}(f_t+dt\ast \frac{\partial f}{\partial x}{v}_t)$

别忘了我们操作的是一个矩阵：

$(I-\frac{d{t}^2}{M}\frac{\partial f}{\partial x}-\frac{dt}{M}\frac{\partial f}{\partial v})△v=\frac{dt}{M}(f_t+dt\ast \frac{\partial f}{\partial x}{v}_t)$

两边乘以M：

$(M-d{t}^2\frac{\partial f}{\partial x}-dt\frac{\partial f}{\partial v})△v=dt(f_t+dt\ast \frac{\partial f}{\partial x}{v}_t)$

解隐式积分需要求解上述的线性方程组，并解出△v。

其中$\frac{\partial f}{\partial x}$和$\frac{\partial f}{\partial v}$的计算方法在参考文献中写的很清楚，这里直接给出结果：

---

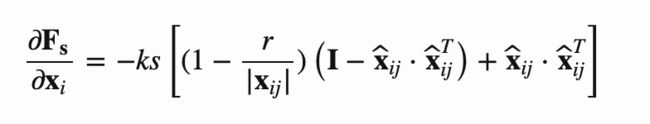
雅克比迭代

在隐式方法中，最终需要求解的线性方程组往往是一个巨大的稀疏矩阵，因此很难通过矩阵求逆的方式求解，这里介绍最简单的迭代求解线性方程组的方法——雅克比迭代。

---

实例代码

弹簧质点系统的显式方法

弹簧质点系统的隐式方法

代码由python语言以及taichi框架编写而成。

单击鼠标添加质点，相邻质点自动添加弹簧，其中红色弹簧表示伸长中，绿色弹簧表示收缩中。

---

公式和求导部分参考
隐式方法推导部分参考
雅克比迭代部分参考