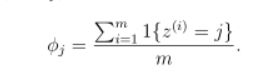朴素贝叶斯.Laplace平滑.多项式事件模型

《Andrew Ng 机器学习笔记》这一系列文章文章是我再观看Andrew Ng的Stanford公开课之后自己整理的一些笔记，除了整理出课件中的主要知识点，另外还有一些自己对课件内容的理解。同时也参考了很多优秀博文，希望大家共同讨论，共同进步。

 

网易公开课地址：http://open.163.com/special/opencourse/machinelearning.html

参考博文：http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html（朴素贝叶斯分类）

               http://blog.sina.com.cn/s/blog_8a951ceb0102wbbv.html

 

 

本篇博文涉及课程五：朴素贝叶斯算法

 

本课主要内容有：

（1）朴素贝叶斯算法

（2）Laplace平滑

（3）多项式事件模型

朴素贝叶斯算法（NB）

 

在GDA模型中，特征向量x是连续的实数向量，当x是离散值时，我们就需要采用朴素贝叶斯算法。

朴素贝叶斯的思想：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

朴素贝叶斯算法的应用，最常见的是文本分类问题，例如邮件是否为垃圾邮件。

对于文本分类问题来说，使用向量空间模型（vector space model,VSM）来表示文本。

什么是向量空间模型？

首先，我们需要有一个词典，词典的来源可以是现有的词典，也可以是从数据中统计出来的词典，对于每个文本，我们用长度等于词典大小的向量表示，如果文本包含某个词，该词在词典中的索引为index，则表示文本的向量的index出设为1，否则为0。

下面以垃圾邮件分类问题为例进行说明：

将邮件作为输入特征，与已有的词典进行比对，如果出现了该词，则把向量的xi=1,否则xi=0,例如： 
                                                                          
我们要对p(x|y)建模，但是假设我们的词典有50000个词，那么，如果采用多项式建模的方式，会有个参数，参数太多了。因此，为了对p(x|y)建模，我们做一个假设，称为朴素贝叶斯假设，由朴素贝叶斯假设推导出的分类器叫做朴素贝叶斯分类器。朴素贝叶斯假设是：假设给定分类y后，特征向量中的各个分量xi是条件独立(conditionally independent）的。也就是说，朴素贝叶斯假设在文本分类问题上是说，文本中出现的某个单词时不会影响其它单词在文本中出现的概率。

因此有： 
                                                         

模型参数包括：

极大似然函数的对数函数为： 
                                                                
得到参数的最大似然估计值： 
                                                              

对于新样本，我们就可以按照如下公式计算其概率值：

                                         

Laplace平滑

朴素贝叶斯存在的问题： 
假设在一封邮件中出现了一个以前邮件从来没有出现的词，在词典的位置是35000，那么得出的最大似然估计为： 

 
                                                 

也就是说，如果一个单词在之前的垃圾邮件和非垃圾邮件中都部曾出现过，那么，朴素贝叶斯模型认为这个词在任何一封邮件出现的概率为0. 
如果，这封邮件是一封垃圾邮件，但通过公式得到的是：
                                          

这样得到的结果并不是很合理，因为我们不能因为某个事件过去没有出现过，就判断该事件出现的概率为0,。

拉普拉斯平滑（Laplace Smoothing）又被称为加1平滑，是比较常用的平滑方法。平滑方法的存在是为了解决零概率问题。、

 

Laplace的解决方法是：

对于一个随机变量z，它的取值范围是{1,2,3...,k}，对于m次试验的观测结果{z(1),z(2),...z(m))}，极大似然估计按照下式计算：

                                                    

使用了Laplace之后：

                                                                     

即在分子上+1，在分母上+变量能取到的个数。

因此，在朴素贝叶斯问题，通过laplace平滑修正后： 

                                                                 

多项式事件分布

上面的这种基本的朴素贝叶斯模型叫做多元伯努利事件模型，该模型有多种扩展，一种是每个分量的多值化，即将p(xi|y)由伯努利分布扩展到多项式分布；还有一种是将连续变量值离散化。例如以房屋面积为例：

                                

 

还有一种，与多元伯努利有较大区别的朴素贝叶斯模型，就是多项式事件模型。

 

多项式事件模型改变了特征向量的表示方法：

在多元伯努利模型中，特征向量的每个分量代表词典中该index上的词语是否在文本中出现过，其取值范围为{0,1}，特征向量的长度为词典的大小。

而在多项式事件模型中，特征向量中的每个分量的值是文本中处于该分量位置的单词在词典中的索引，其取值范围是{1,2,...,|V|}，|V|是词典的大小，特征向量的长度为文本中单词的数量。

例如：在多元伯努利模型下，一篇文本的特征向量可能如下：

                                                                          

在多项式事件模型下，这篇文本的特征向量为：

                                                                      

一篇文本产生的过程是：

1、确定文本类别

2、以相同的多项式分布在各个位置上生成词语。

例如：x1是由服从p(x1|y)的多项式分布产生的，x2是独立与x1的并且来自于同一个多项式分布，同样的，产生x3,x4，一直到xn。

因此，所有的这个信息的概率是. 

模型的参数为： 
                                                                                         
                                                                                        
                                                                                        

 

参数在训练集上的极大似然函数： 
                                                      

参数的最大似然估计为： 
                                                      

应用laplace平滑，分子加1，分母加|V|，得到： 
                                                    

对于式子：

                                                        

分子的意思是对训练集合中的所有垃圾邮件中词k出现的次数进行求和。

分母的含义是对训练样本集合进行求和，如果其中的一个样本是垃圾邮件（y=1），那么就把它的长度加起来，所以分母的含义是训练集合中所有垃圾邮件的词语总长。

所以这个比值的含义就是在所有垃圾邮件中，词k所占的比例。

注意这个公式与多元伯努利的不同在于：这里针对整体样本求的φk|y=1 ，而多远伯努利里面针对每个特征求的φxj=1|y=1 ，而且这里的特征值维度不一定是相同的。

举例说明多项式事件模型：
假设邮件中有a,b,c三个词，他们在词典的位置分别是1,2,3,第一封里面内容为a,b，第二封为b,a;第三封为a,c,b,第四封为c,c,c。

Y=1是垃圾邮件。
因此，我们有：

那么，我们可得：

假如有一封信的邮件，内容为b,c。那么它的特征向量为{2,3},我们可得：

那么该邮件为垃圾邮件概率是0.6。