算法笔记——左神初级(2)快速排序、堆排序
快速排序
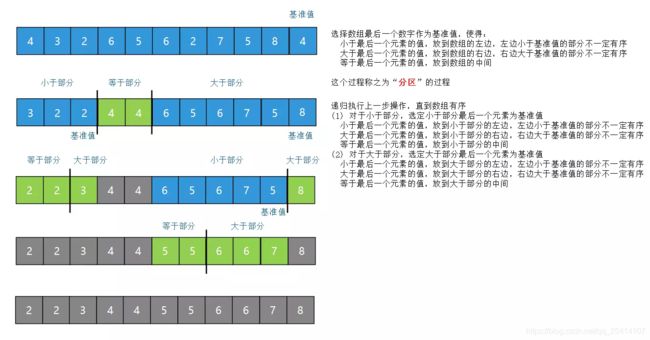
快速排序的核心思想是按基准值分区:
荷兰国旗问题:
public static int[] partition(int[] arr, int L, int R, int p) {
int less = L - 1;
int more = R + 1;
while (L < more) {
if (arr[L] < p) {
swap(arr, ++less, L++);
} else if (arr[L] > p) {
swap(arr, --more, L);
} else {
L++;
}
}
return new int[] {
less + 1, more - 1 };
}
返回的是等于基准值的数字在数组中的位置。
快排代码
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int L, int R) {
if (L < R) {
//swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
int[] p = partition(arr, L, R);
quickSort(arr, L, p[0] - 1);
quickSort(arr, p[1] + 1, R);
}
}
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);
} else {
l++;
}
}
swap(arr, more, r);
return new int[] {
less + 1, more };
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
这是改进后的经典快排。可以看到partition函数会返回除基准值以外的数,而对基准值做了保留(这里基准值指的是若干个相等的数!) 而经典快排,一次只搞定一个数,也就是把初始的右侧数作为基准放中间,小于等于放左边,大于放右边。这样会导致左边会包含等于基准值的若干个数。 虽然复杂度相同,但常数时间会有差距。
可以看见快排的核心函数是partiton函数,该函数的作用是把输入数组的右侧数据用来做基准值,对数据进行快排,返回基准值的左边部分(比基准值小)和右边部分(比基准值大),再对左右部分进行partition。嵌套,最终对数组完成排序。
经典快排的问题是他的效率会和数据状况有关系,
参考master公式

具体原因是经典快排可能导致子区域划分极不平均。
经典快排的复杂度
最好的情况复杂度为T(N)=2T(N/2)+O(N),否则复杂度较高。
随机快速排序
所以随机快排是从数组中间取出一个数放到最右边,再进行快排。
随机快排和上面的经典快排代码基本相同,唯一区别如下。
public static void quickSort(int[] arr, int L, int R) {
if (L < R) {
swap(arr, L + (int) (Math.random() * (R - L + 1)), R); //先随机取出一个数放到最后
int[] p = partition(arr, L, R);
quickSort(arr, L, p[0] - 1);
quickSort(arr, p[1] + 1, R);
}
}
随机快排复杂度
期望复杂度:O(N*logN),额外空间复杂度为O(logN)
这个额外空间复杂度的来源是记录的断点位置,能被二分多少次,就需要存多少个。这是长期期望的概率,否则最差的情况额外复杂度为O(N)。
工程上需要改成非递归版本~~
堆结构
堆的结构就是一棵完全二叉树;
完全二叉树就是从树的每层从左往右依次补全
完全二叉树是由满二叉树而引出来的,若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树),第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
堆一般都是用完全二叉树来实现的。
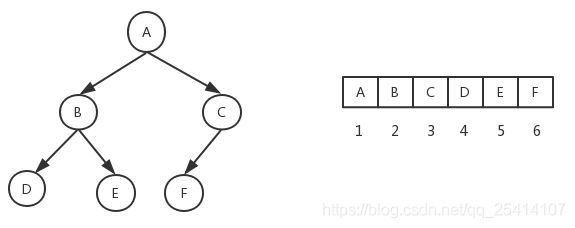
左孩子: 2i+1; 右孩子:2i+2
父节点:(i-1)/2
大根堆:任何一颗子树的最大值都是这个子树的头部
小根堆:任何一颗子树的最小值都是这个子树的头部
怎样建立一个大根堆?
代码如下:(加入一个新节点往上调整的函数——heapInsert)
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
//如果大于父节点
swap(arr, index, (index - 1) / 2); //交换其和父节点的位置
index = (index - 1) / 2; //再将新的父节点与它的父节点比较,循环
}
}
上述过程中,arr是待排序的数组,i(index)之前已经排好了大根堆,i指的是排好的大根堆中的下个数的索引。
如果 i 索引的数大于父节点,交换其和父节点的位置,再将新的父节点与它的父节点比较,循环
如果 i 索引的数不大于父节点,i++
建立一个大根堆的时间复杂度
注意,一个新节点 i 加入进来,最多比较的次数其实就是高度,也即是log(i-1)
所以建立一个大根堆的时间复杂度为
log1+log2+log3+……+log(N-1) = O(N)
当大根堆里的数变化后,怎么维持大根堆结构?
heapify函数
heapsize是指这个堆的大小(最大不超过数组长度)
public static void heapify(int[] arr, int index, int heapsize) {
int left = index * 2 + 1;
while (left < heapsize) {
//左孩子没有越界
int largest = left + 1 < heapsize && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index; //左右孩子最大值和我自身作比较
if (largest == index) {
//不用往下沉了
break;
}
swap(arr, largest, index); //否则往下沉
index = largest;
left = index * 2 + 1;
}
}
小结
建立大根堆的过程使用的函数为heapInsert,
当大根堆里的数变化后,维持大根堆结构函数为heapify,
堆数据可以增加也可以减少,堆数据增加可以使用heapInsert,
堆数据减少时将根节点弹出,最后节点放到根节点,再进行heapify
堆在系统中一般称呼叫优先级队列,调整代价较小,只需要承担logN的复杂度就可以完成,非常重要
例子:求输出若干数后的中位数
一个数列不断增加,需要随时求所有数的中位数,可以使用堆进行运算(分成大根堆和小根堆)
算法流程:
1.首先创建两个堆,一个大根堆,一个小根堆 (大根堆里装较小的数,小根堆里装大的数)
2.将第一个数据防入大根堆
3.将下一个数据跟大根堆中的数据进行比较,如果数据小于大根堆中的根,则放入大根堆中,否则装入小根堆中。
4.如果大根堆和小根堆中的数目相差2,则将数据较多的堆的父节点弹出,放入数据较少的数据堆中当父节点。弹出根节点的堆,将堆底的数放到堆顶,然后执行响应的heapify操作,同时heapsize减一。接收节点的堆采用heapinsert操作。 回到步骤3 。
中位数的数据只会从大根堆和小根堆的父节点中选出,随时进入数据,则可以随时调整,复杂度较低。
堆排序
步骤:
1、全部形成大根堆
2、堆顶跟最后数交换
3、heapsize减一(最大的数就被留到了最后)
4、对根节点进行heapify操作,重新生成大根堆
5、回到步骤2,直到排完。
代码如下:
public class Code_03_HeapSort {
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
int size = arr.length;
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
public static void heapify(int[] arr, int index, int heapsize) {
int left = index * 2 + 1;
while (left < heapsize) {
//左孩子没有越界
int largest = left + 1 < heapsize && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index; //左右孩子最大值和我自身作比较
if (largest == index) {
//我比左右孩子大,不用往下沉了
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}