运算放大器在超高频信号作用下的偏移量的变化
在下面推文中,对于集成运算放大器在强电磁干扰环境下出现的变化进行了实验展示研究。下面讨论一下,究竟其集成运算放大器收到外部输入信号的影响,与输入信号的频率有什么关系?为什么在平时放大普通中低频型号的时候,没有讨论运算放大器对于电磁干扰的频率有什么关系,下面就实验展开讨论。
- 运算放大器在强电磁干扰下出现什么变化?
运放在高频信号作用下,通常情况下应该有它的频率特性所决定。即随着输入信号的频率的变化,输出信号的幅值和相位所产生的变化。分别称为放大电路的幅频特性和相频特性。由如下表达式给出:
G ( j ω ) = ∣ G ( j ω ) ∣ ⋅ e j φ ( j ω ) G\left( {j\omega } \right) = \left| {G\left( {j\omega } \right)} \right| \cdot e^{j\varphi \left( {j\omega } \right)} G(jω)=∣G(jω)∣⋅ejφ(jω)
其中 ∣ G ( j ω ) ∣ \left| {G\left( {j\omega } \right)} \right| ∣G(jω)∣是幅频特性; φ ( j ω ) \varphi \left( {j\omega } \right) φ(jω)是相频特性。
LM386在高频信号作用下的变化
实验方案
使用DS345产生所0.1~30MHz的输入信号,测量LM386的输出信号的波形、交流有效值以及直流分量的大小。
直流分量使用FLUKE45万用表来测量。
产生0.1~30MHz的输入信号
通过测量300个数据,分别获得测量数据:
- offset: LM386电路的输出直流分的
- freq: 信号的频率;
- vrms:LM386输出的交流有效值
具体的输入如下面所示:
'lm386freq'.nzp:
'offset': [2.4303 2.4225 2.4076 2.3862 2.3651 2.3521 2.3428 2.3355 2.3297 2.3259
2.3237 2.3227 2.3231 2.3239 2.3253 2.3273 2.3295 2.3319 2.3347 2.3368
2.3391 2.3412 2.3429 2.3445 2.346 2.3465 2.3466 2.3467 2.346 2.3451
2.3436 2.3419 2.3392 2.3361 2.333 2.3299 2.3261 2.3224 2.3186 2.315
2.3114 2.3075 2.3037 2.3003 2.297 2.2941 2.2914 2.2887 2.286 2.2842
2.282 2.2801 2.279 2.2772 2.2762 2.2749 2.2745 2.2733 2.2728 2.2727
2.272 2.2719 2.2721 2.2724 2.2724 2.273 2.2736 2.274 2.275 2.2758
2.2758 2.2768 2.2774 2.2784 2.2797 2.2801 2.2812 2.2819 2.2831 2.2842
2.2852 2.2865 2.2878 2.2892 2.2903 2.2915 2.2926 2.2936 2.2948 2.2959
2.2971 2.2982 2.2994 2.3006 2.3018 2.3031 2.3042 2.3053 2.3067 2.308
2.309 2.31 2.3111 2.3123 2.3135 2.3146 2.3156 2.3167 2.3178 2.3189
2.32 2.3211 2.3219 2.3231 2.3241 2.3252 2.3262 2.3274 2.3283 2.3289
2.3299 2.3309 2.3317 2.3327 2.3337 2.3346 2.3356 2.3366 2.3376 2.3386
2.3395 2.3403 2.3412 2.3421 2.3429 2.3438 2.3446 2.3455 2.3464 2.3472
2.348 2.3489 2.3495 2.3502 2.351 2.3517 2.3524 2.3531 2.3539 2.3547
2.3553 2.356 2.3567 2.3574 2.358 2.3587 2.3593 2.3597 2.3604 2.361
2.3617 2.3624 2.3631 2.3638 2.3643 2.365 2.3656 2.3663 2.367 2.3676
2.3682 2.3688 2.3692 2.3697 2.3703 2.3706 2.3711 2.3715 2.3721 2.3727
2.3732 2.3737 2.3742 2.3748 2.3754 2.3759 2.3765 2.3771 2.3774 2.378
2.3785 2.3791 2.3796 2.38 2.3806 2.381 2.3816 2.382 2.3823 2.3829
2.3831 2.3836 2.3842 2.3846 2.385 2.3855 2.3859 2.3864 2.3868 2.3872
2.3876 2.3879 2.3883 2.3887 2.3891 2.3894 2.3896 2.3899 2.3904 2.3906
2.3911 2.3913 2.3917 2.3922 2.3924 2.3927 2.3929 2.3932 2.3934 2.3938
2.3942 2.3944 2.3946 2.3949 2.3951 2.3954 2.3956 2.396 2.3961 2.3965
2.3965 2.397 2.3972 2.3973 2.3975 2.3977 2.398 2.3982 2.3986 2.3989
2.3989 2.3991 2.3992 2.3995 2.3998 2.4 2.4002 2.4003 2.4005 2.4007
2.401 2.4012 2.4015 2.4017 2.4018 2.4019 2.4022 2.4024 2.4026 2.4028
2.4029 2.4031 2.4031 2.4034 2.4037 2.4036 2.4038 2.4039 2.404 2.4042
2.4043 2.4046 2.4044 2.4046 2.4047 2.4048 2.4051 2.4052 2.4052 2.4053
2.4054 2.4055 2.4056 2.4056 2.4057 2.4058 2.406 2.4061 2.4062 2.4064]
'freq': [ 100000. 200000. 300000. 400000. 500000. 600000. 700000.
800000. 900000. 1000000. 1100000. 1200000. 1300000. 1400000.
1500000. 1600000. 1700000. 1800000. 1900000. 2000000. 2100000.
2200000. 2300000. 2400000. 2500000. 2600000. 2700000. 2800000.
2900000. 3000000. 3100000. 3200000. 3300000. 3400000. 3500000.
3600000. 3700000. 3800000. 3900000. 4000000. 4100000. 4200000.
4300000. 4400000. 4500000. 4600000. 4700000. 4800000. 4900000.
5000000. 5100000. 5200000. 5300000. 5400000. 5500000. 5600000.
5700000. 5800000. 5900000. 6000000. 6100000. 6200000. 6300000.
6400000. 6500000. 6600000. 6700000. 6800000. 6900000. 7000000.
7100000. 7200000. 7300000. 7400000. 7500000. 7600000. 7700000.
7800000. 7900000. 8000000. 8100000. 8200000. 8300000. 8400000.
8500000. 8600000. 8700000. 8800000. 8900000. 9000000. 9100000.
9200000. 9300000. 9400000. 9500000. 9600000. 9700000. 9800000.
9900000. 10000000. 10100000. 10200000. 10300000. 10400000. 10500000.
10600000. 10700000. 10800000. 10900000. 11000000. 11100000. 11200000.
11300000. 11400000. 11500000. 11600000. 11700000. 11800000. 11900000.
12000000. 12100000. 12200000. 12300000. 12400000. 12500000. 12600000.
12700000. 12800000. 12900000. 13000000. 13100000. 13200000. 13300000.
13400000. 13500000. 13600000. 13700000. 13800000. 13900000. 14000000.
14100000. 14200000. 14300000. 14400000. 14500000. 14600000. 14700000.
14800000. 14900000. 15000000. 15100000. 15200000. 15300000. 15400000.
15500000. 15600000. 15700000. 15800000. 15900000. 16000000. 16100000.
16200000. 16300000. 16400000. 16500000. 16600000. 16700000. 16800000.
16900000. 17000000. 17100000. 17200000. 17300000. 17400000. 17500000.
17600000. 17700000. 17800000. 17900000. 18000000. 18100000. 18200000.
18300000. 18400000. 18500000. 18600000. 18700000. 18800000. 18900000.
19000000. 19100000. 19200000. 19300000. 19400000. 19500000. 19600000.
19700000. 19800000. 19900000. 20000000. 20100000. 20200000. 20300000.
20400000. 20500000. 20600000. 20700000. 20800000. 20900000. 21000000.
21100000. 21200000. 21300000. 21400000. 21500000. 21600000. 21700000.
21800000. 21900000. 22000000. 22100000. 22200000. 22300000. 22400000.
22500000. 22600000. 22700000. 22800000. 22900000. 23000000. 23100000.
23200000. 23300000. 23400000. 23500000. 23600000. 23700000. 23800000.
23900000. 24000000. 24100000. 24200000. 24300000. 24400000. 24500000.
24600000. 24700000. 24800000. 24900000. 25000000. 25100000. 25200000.
25300000. 25400000. 25500000. 25600000. 25700000. 25800000. 25900000.
26000000. 26100000. 26200000. 26300000. 26400000. 26500000. 26600000.
26700000. 26800000. 26900000. 27000000. 27100000. 27200000. 27300000.
27400000. 27500000. 27600000. 27700000. 27800000. 27900000. 28000000.
28100000. 28200000. 28300000. 28400000. 28500000. 28600000. 28700000.
28800000. 28900000. 29000000. 29100000. 29200000. 29300000. 29400000.
29500000. 29600000. 29700000. 29800000. 29900000. 30000000.]
'vrms': ['6.413334e-01' '6.825742e-01' '6.430228e-01' '6.115741e-01'
'5.237851e-01' '4.306417e-01' '3.639022e-01' '3.009561e-01'
'2.553482e-01' '2.161986e-01' '1.855373e-01' '9.9e37' '1.391495e-01'
'1.218520e-01' '1.072661e-01' '9.524767e-02' '8.445734e-02'
'7.634338e-02' '6.804499e-02' '6.211770e-02' '5.639556e-02'
'5.104101e-02' '4.643925e-02' '4.229035e-02' '4.033240e-02'
'3.588475e-02' '3.417603e-02' '3.186109e-02' '2.938205e-02'
'2.898289e-02' '2.602621e-02' '2.434417e-02' '2.256209e-02'
'2.406842e-02' '2.168857e-02' '1.981758e-02' '1.902001e-02'
'1.827843e-02' '1.883330e-02' '1.920945e-02' '1.781426e-02'
'1.697402e-02' '1.740047e-02' '1.711480e-02' '1.817070e-02'
'1.688382e-02' '1.722660e-02' '1.896028e-02' '1.566125e-02'
'1.589628e-02' '1.782895e-02' '1.648637e-02' '1.586606e-02'
'1.815148e-02' '1.591548e-02' '1.630543e-02' '1.584955e-02'
'1.656557e-02' '1.636419e-02' '1.640945e-02' '1.530338e-02'
'1.835703e-02' '1.570021e-02' '1.613599e-02' '1.768892e-02'
'1.836890e-02' '1.568074e-02' '1.770125e-02' '1.435609e-02'
'1.610622e-02' '1.843055e-02' '1.760238e-02' '1.514577e-02'
'1.832848e-02' '1.510828e-02' '1.563616e-02' '1.623303e-02'
'1.907270e-02' '1.735528e-02' '1.453428e-02' '1.600568e-02'
'1.473698e-02' '1.634819e-02' '1.639349e-02' '1.738040e-02'
'1.615760e-02' '1.704584e-02' '1.928652e-02' '1.933171e-02'
'1.600841e-02' '1.725696e-02' '1.714791e-02' '1.705095e-02'
'1.703559e-02' '1.559426e-02' '1.773080e-02' '1.420025e-02'
'1.471328e-02' '1.426463e-02' '1.490184e-02' '1.906812e-02'
'1.586331e-02' '1.726202e-02' '1.560824e-02' '1.755771e-02'
'1.763705e-02' '1.563616e-02' '1.773818e-02' '1.885645e-02'
'1.688382e-02' '1.513425e-02' '1.355902e-02' '1.562221e-02'
'1.452527e-02' '1.470142e-02' '1.838552e-02' '1.733515e-02'
'1.681910e-02' '1.578059e-02' '1.435305e-02' '1.421254e-02'
'1.463598e-02' '1.664439e-02' '1.750795e-02' '1.768152e-02'
'1.647579e-02' '1.802123e-02' '1.777012e-02' '1.562779e-02'
'1.924349e-02' '1.558586e-02' '1.556906e-02' '1.787538e-02'
'1.739796e-02' '1.845894e-02' '1.832848e-02' '1.998419e-02'
'1.894877e-02' '1.620075e-02' '1.787538e-02' '1.480197e-02'
'1.535745e-02' '1.833562e-02' '1.620075e-02' '1.496320e-02'
'1.512271e-02' '1.571687e-02' '1.704071e-02' '1.746803e-02'
'1.726454e-02' '1.634018e-02' '1.718603e-02' '1.673328e-02'
'1.568353e-02' '1.705607e-02' '1.472217e-02' '1.615760e-02'
'1.427074e-02' '1.595381e-02' '1.518892e-02' '1.574183e-02'
'1.729988e-02' '1.423708e-02' '1.700996e-02' '1.528627e-02'
'1.662866e-02' '1.623034e-02' '1.789246e-02' '1.584680e-02'
'1.807923e-02' '1.463896e-02' '1.726960e-02' '1.668105e-02'
'1.732257e-02' '1.726960e-02' '1.686055e-02' '1.556906e-02'
'1.588804e-02' '1.729988e-02' '1.740799e-02' '1.392727e-02'
'1.815389e-02' '1.652074e-02' '1.637485e-02' '1.721646e-02'
'1.625988e-02' '1.783384e-02' '1.599750e-02' '1.734773e-02'
'1.649167e-02' '1.500687e-02' '1.592644e-02' '1.537165e-02'
'1.484024e-02' '1.766177e-02' '1.536597e-02' '1.516305e-02'
'1.705863e-02' '1.541699e-02' '1.551291e-02' '1.594834e-02'
'1.654185e-02' '1.809853e-02' '1.600023e-02' '1.674891e-02'
'1.803816e-02' '1.661291e-02' '1.679054e-02' '1.618189e-02'
'1.525198e-02' '1.697145e-02' '1.604380e-02' '1.563895e-02'
'1.896948e-02' '1.475769e-02' '1.744554e-02' '1.544244e-02'
'1.654185e-02' '1.548194e-02' '1.831896e-02' '1.586881e-02'
'1.716825e-02' '1.650753e-02' '1.638285e-02' '1.663653e-02'
'1.598932e-02' '1.640148e-02' '1.526628e-02' '1.508516e-02'
'1.709439e-02' '1.531193e-02' '1.697916e-02' '2.061604e-02'
'1.571409e-02' '1.753285e-02' '1.666011e-02' '1.679573e-02'
'1.670196e-02' '1.534324e-02' '1.789246e-02' '1.589902e-02'
'1.411706e-02' '1.590999e-02' '1.437431e-02' '1.690448e-02'
'1.590725e-02' '1.749299e-02' '1.696116e-02' '1.610893e-02'
'1.856499e-02' '1.580545e-02' '1.881012e-02' '1.388020e-02'
'1.765436e-02' '1.473698e-02' '1.424014e-02' '1.561383e-02'
'1.472514e-02' '1.817070e-02' '1.694572e-02' '1.643602e-02'
'1.635086e-02' '1.599477e-02' '1.540567e-02' '1.604652e-02'
'1.575845e-02' '1.554943e-02' '1.484905e-02' '1.603019e-02'
'1.787782e-02' '1.617110e-02' '1.656821e-02' '1.565011e-02'
'1.675673e-02' '1.706630e-02' '1.576676e-02' '1.604652e-02'
'1.649696e-02' '1.559426e-02' '1.677494e-02' '1.705863e-02'
'1.576399e-02' '1.402093e-02' '1.788514e-02' '1.444999e-02'
'1.695344e-02' '1.631346e-02' '1.474290e-02' '1.624646e-02'
'1.591274e-02' '1.575845e-02' '1.528341e-02' '1.881244e-02'
'1.746553e-02' '1.680612e-02' '1.845184e-02' '1.784607e-02'
'1.692511e-02' '1.857204e-02' '1.447412e-02']
结果分析
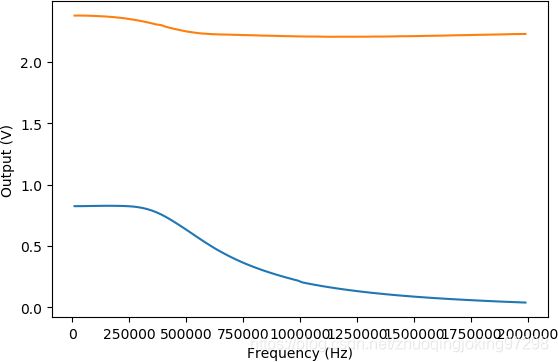
(1)随着输入频率的变化,LM386的输出直流分量的变化如下。
这个变化首先随着频率不是线性单调的变化。在6MHz附近,直流分量达到最小。这个的幅值变化都在0.25V之间。
 LM385输出质量分量随着频率变化而变化的曲线
LM385输出质量分量随着频率变化而变化的曲线
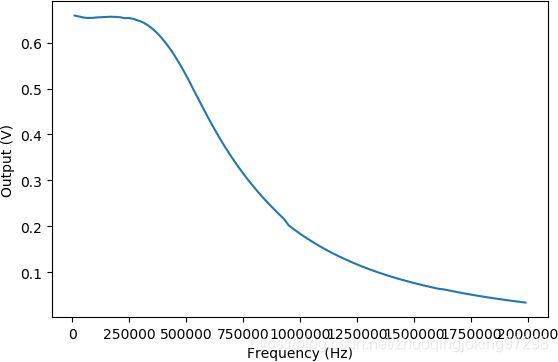
下图显示了LM386的幅频特性。对照上面的直流分量的变化,可以看到直流分量的变化发生在LM386 的通带范围之外。
 LM386输出信号的幅值随着频率的变化
LM386输出信号的幅值随着频率的变化
从上面的结果看到,运放在高频作用下,对应的结果变化实际上并不是太明显?
那么为什么如何解释当频率达到了400Mhz以上的对讲机的频率时,输出的DC变化就非常大了呢?
这的确是一个非常有趣的问题。