KMP算法学习分享
问题:
文本串 S = “BBC ABCDAB ABCDABCDABDE”
模式串 P = “ABCDABD”
找出 P 在 S 中的位置。
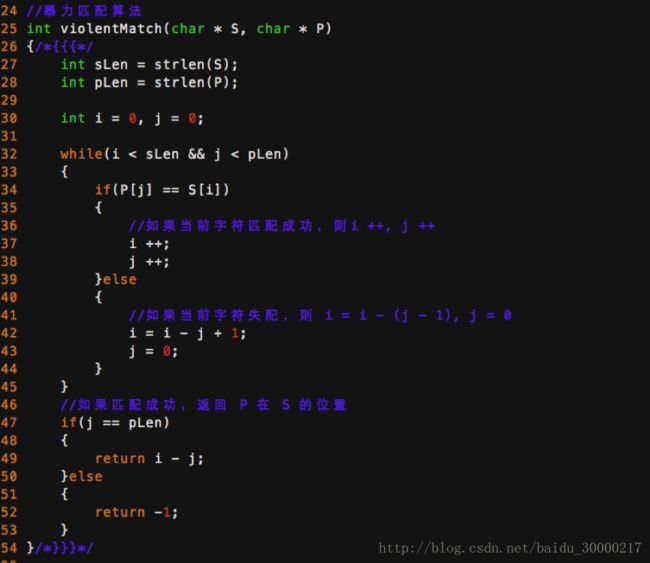
一、 暴力匹配算法:
过程分析:
1、 S[0]为B,P[0]为A,不匹配,则 i往后移动一位,j 回到开头,即 i = i – j + 1, j = 0。相当于模式串往右移动一位(i = 1,j = 0)
2、 S[1]跟P[0]还是不匹配,则 i往后移动一位,j 回到开头,即 i = i – j + 1, j = 0。(i = 2,j = 0)
3、 一直执行以上过程,直到S[4]跟P[0]匹配成功(i=4,j=0),此时 i ++,j ++
4、 发现后六个字母是相等的,直到S[10]为空格字符,P[6]为字符D(i=10,j=6),因为不匹配,此时执行 i = i – j + 1 = 5, j = 0。
5、 i = 5,j = 0,即i 和 j 回溯,从新比较:
思考?
前面都对比过了,后面再重复这个过程干嘛!
解决方案:
KMP算法:利用之前已经部分匹配这个有效信息,保持i 不回溯,通过修改j 的位置,让模式串尽量地移动到有效的位置。
Knuth-Morris-Pratt 字符串查找算法,简称为 “KMP算法”(民间:“看毛片儿算法“),常用于在一个文本串S内查找一个模式串P 的出现位置,这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表,故取这3人的姓氏命名此算法。
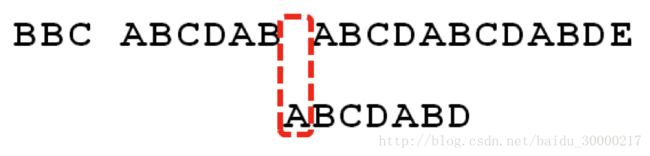
再看最后一张图片:
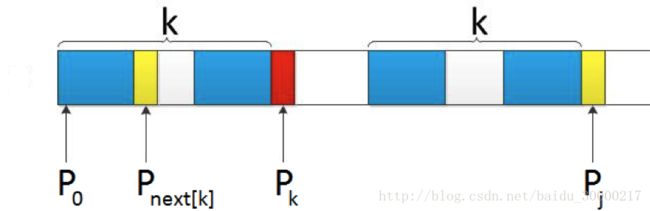
一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是”ABCDAB”。KMP算法的想法是,设法利用这个已知信息,不要把”搜索位置”移回已经比较过的位置,继续把它向后移,这样就提高了效率。
在这里我们先给出一个 next 数组,先别管怎么求吧,先用:
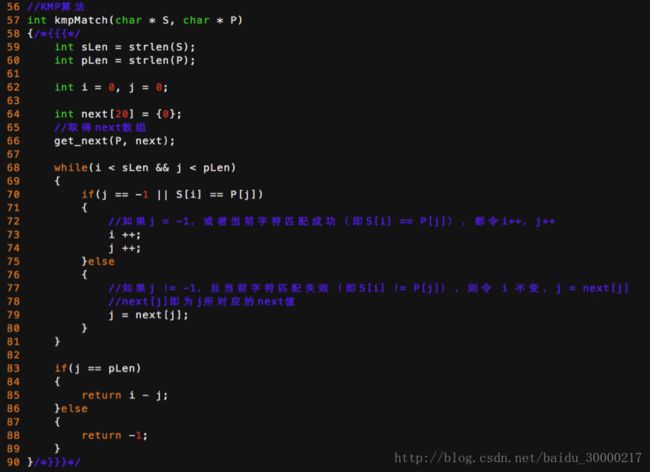
KMP算法代码如下:
继续拿之前的例子来说,当S[10]跟P[6]匹配失败时,KMP不是跟暴力匹配那样简单的把模式串右移一位,而是执行j = next[j]:“如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]”,即j 从6变到2(后面我们将求得P[6],即字符D对应的next 值为2),所以相当于模式串向右移动的位数为j - next[j](j - next[j] = 6-2 = 4)。
向右移动4位后,S[10]跟P[2]继续匹配。为什么要向右移动4位呢,因为移动4位后,模式串中又有个“AB”可以继续跟S[8]S[9]对应着,从而不用让i 回溯。相当于在除去字符D的模式串子串中寻找相同的前缀和后缀,然后根据前缀后缀求出next 数组,最后基于next 数组进行匹配
根据next数组,后续的匹配过程应该是这样的:
模式串向右移动4位后,发现C处再度失配,移动位数 = j – next[j] = 2 – 0 = 2
A与空格失配,移动位数 = j – next[j] = 0 – (-1) = 1
继续比较,发现D与C 失配,故向右移动的位数为:已匹配的字符数6减去上一位字符B对应的最大长度2,即向右移动6 - 2 = 4 位。
最终匹配成功,过程结束。
关键来了!!!
next数组咋弄?
稳住了各位,如果上面的过程弄懂了,那求next数组的过程就变得很简单了。
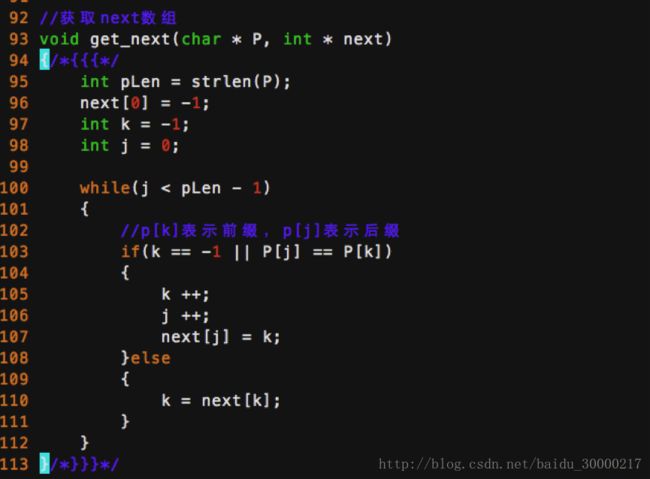
先看代码:
跟kmp算法的代码很像有木有!其实求next数组无非就是模式串本身的自我匹配过程
求next数组的过程,其实是求前缀后缀最长公共元素长度的过程:
对于P = p0 p1 …pj-1 pj,寻找模式串P中长度最大且相等的前缀和后缀。如果存在p0 p1 …pk-1 pk = pj- k pj-k+1…pj-1 pj,那么在包含pj的模式串中有最大长度为k+1的相同前缀后缀。举个例子,如果给定的模式串为“abab”,那么它的各个子串的前缀后缀的公共元素的最大长度如下表格所示:
比如对于字符串aba来说,它有长度为1的相同前缀后缀a;而对于字符串abab来说,它有长度为2的相同前缀后缀ab(相同前缀后缀的长度为k + 1,k + 1 = 2)。
next 数组考虑的是除当前字符外的最长相同前缀后缀,所以通过第①步骤求得各个前缀后缀的公共元素的最大长度后,只要稍作变形即可:将第①步骤中求得的值整体右移一位,然后初值赋为-1,如下表格所示:
比如对于aba来说,第3个字符a之前的字符串ab中有长度为0的相同前缀后缀,所以第3个字符a对应的next值为0;而对于abab来说,第4个字符b之前的字符串aba中有长度为1的相同前缀后缀a,所以第4个字符b对应的next值为1(相同前缀后缀的长度为k,k = 1)。
通过代码分析next数组的求解过程:
1、 已知前一步计算时最大相同的前后缀长度为k(k>0),即P[0]···P[k-1];
也就是对于值k,已有p0 p1, …, pk-1 = pj-k pj-k+1, …, pj-1,相当于next[j] = k。
此意味着什么呢?究其本质,next[j] = k 代表p[j] 之前的模式串子串中,有长度为k 的相同前缀和后缀
2、 下面的问题是:已知next [0, …, j],如何求出next [j + 1]呢?
对于P的前j+1个序列字符:
• 若p[k] == p[j],则next[j + 1] = next [j] + 1 = k + 1;
• 若p[k] ≠ p[j],如果此时p[ next[k] ] == p[j],则next[ j + 1 ] = next[k] + 1,否则继续递归前缀索引k = next[k],而后重复此过程。 相当于在字符p[j+1]之前不存在长度为k+1的前缀”p0 p1, …, pk-1 pk”跟后缀“pj-k pj-k+1, …, pj-1 pj”相等,那么是否可能存在另一个值t+1 < k+1,使得长度更小的前缀 “p0 p1, …, pt-1 pt” 等于长度更小的后缀 “pj-t pj-t+1, …, pj-1 pj” 呢?如果存在,那么这个t+1 便是next[ j+1]的值,此相当于利用已经求得的next 数组(next [0, …, k, …, j])进行P串前缀跟P串后缀的匹配。
此过程相当于模式串的自我匹配,所以不断的递归k = next[k],直到要么找到长度更短的相同前缀后缀,要么没有长度更短的相同前缀后缀
KMP算法时间复杂度分析:
分析之前,先来回顾下KMP匹配算法的流程:
“KMP的算法流程:
• 假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置
• 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
• 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。”
我们发现如果某个字符匹配成功,模式串首字符的位置保持不动,仅仅是i++、j++;如果匹配失配,i 不变(即 i 不回溯),模式串会跳过匹配过的next [j]个字符。整个算法最坏的情况是,当模式串首字符位于i - j的位置时才匹配成功,算法结束。
所以,如果文本串的长度为n,模式串的长度为m,那么匹配过程的时间复杂度为O(n),算上计算next的O(m)时间,KMP的整体时间复杂度为O(m + n)。
本文大部分参考资料:《从头到尾彻底理解KMP》