图论模型-Floyd

图论模型-Floyd

应用

Floyd算法主要通过动态规划解决任意两点间的最短路径（多源最短路径）的问题，可以正确处理负权的最短路径问题。

动态规划

和Dijkstra算法的静态规划相比，Floyd算法通过拆分问题规模，并定义问题状态与状态的关系，使得问题能够以递推的方式去解决，最终合并各个拆分的小问题的解为整个问题的解。

解决问题

还是上次的问题，只是这次我们从每一个点到其他点的最短距离和路径，每条边的红色数字代表这条边的长度，那我们如何找到这些信息呢？

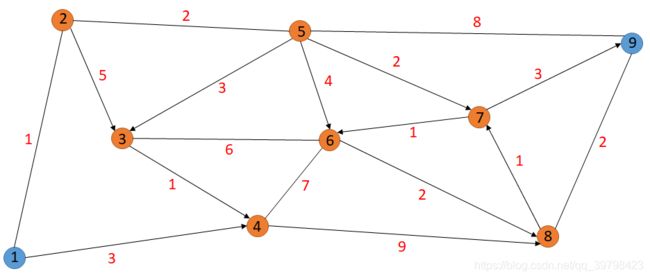
Floyd算法

Floyd算法的关键代码很简单，就是下面的短短4行。主要就是将找一个位置$i$到非常远位置$j$的最短路径变为很多找两个点，比如$i$和$k$，$k$和$z$，$z$和$j$z之间最短路径的问题。

for k in range(0, N):
        for i in range(0, N):
            for j in range(0, N):
            	A[i][j] = min(A[i][j], A[i][k] + A[k][j])

原理

参照floyd算法:我们真的明白floyd吗?

python代码

# 图论模型-Floyd

import numpy as np

inf = 99999  # 不连通值

mtx_graph = [[0,   1,   inf, 3,   inf, inf, inf, inf, inf],
             [1,   0,   5,   inf, 2,   inf, inf, inf, inf],
             [inf, inf, 0,   1,   inf, 6,   inf, inf, inf],
             [inf, inf, inf, 0,   inf, 7,   inf, 9,   inf],
             [inf, 2,   3,   inf, 0,   4,   2,   inf, 8  ],
             [inf, inf, 6,   7,   inf, 0,   inf, 2,   inf],
             [inf, inf, inf, inf, inf, 1,   0,   inf, 3  ],
             [inf, inf, inf, inf, inf, inf, 1,   0,   2  ],
             [inf, inf, inf, inf, 8,   inf, 3,   2,   0  ]]  # 带权连接矩阵

def Floyd(graph):
    N = len(graph)
    A = np.array(graph)
    path = np.zeros((N, N))
 
    for i in range(0, N):
        for j in range(0, N):
            if A[i][j] != inf:
                path[i][j] = j
                
    for k in range(0, N):
        for i in range(0, N):
            for j in range(0, N):
                if A[i][k] + A[k][j] < A[i][j]: 
                    A[i][j] = A[i][k] + A[k][j]
                    path[i][j] = path[i][k]
    
    for i in range(0, N):
        for j in range(0, N):
            path[i][j] = path[i][j] + 1

    print('距离 = ')
    print(A)
    print('路径 = ')
    print(path)

Floyd(mtx_graph)

输出如下

距离 = 
[[ 0  1  6  3  3  6  5  8  8]
 [ 1  0  5  4  2  5  4  7  7]
 [21 20  0  1 18  6  9  8 10]
 [22 21 13  0 19  7 10  9 11]
 [ 3  2  3  4  0  3  2  5  5]
 [15 14  6  7 12  0  3  2  4]
 [14 13  7  8 11  1  0  3  3]
 [13 12  8  9 10  2  1  0  2]
 [11 10 10 11  8  4  3  2  0]]

路径 = 
[[1. 2. 2. 4. 2. 2. 2. 2. 2.]
 [1. 2. 3. 1. 5. 5. 5. 5. 5.]
 [6. 6. 3. 4. 6. 6. 6. 6. 6.]
 [8. 8. 6. 4. 8. 6. 8. 8. 8.]
 [2. 2. 3. 3. 5. 7. 7. 7. 7.]
 [8. 8. 3. 4. 8. 6. 8. 8. 8.]
 [9. 9. 6. 6. 9. 6. 7. 6. 9.]
 [9. 9. 7. 7. 9. 7. 7. 8. 9.]
 [5. 5. 7. 7. 5. 7. 7. 8. 9.]]

根据结果的矩阵可以看出

• 从①到⑨的距离为8（距离矩阵第一行第九列的数值）
• 路径为【1 - 2 - 5 - 7 - 8 - 9】（看距离矩阵，从①到⑨看第一行第九列的数值为2，这是中间位置②，再转到第二行第九列看数值为5，得到第二个中间位置⑤，再转到第五行第九列，一直找到⑨，就能得到路径为【1 - 2 - 5 - 7 - 8 - 9】）
  对比Dijkstra算法对这个问题得到的解，相互验证。