传感器响应时间与滤波器截止频率的关系
文章目录
- 一、传感器的响应时间
- 二、传感器响应时间与滤波器截止频率的关系
-
- 2.1、信号的带宽计算公式
- 2.2、`0.35`是怎么来的
- 2.3、RC充电时间常数
- 三、Multisim仿真
-
- 3.1、信号的带宽
- 3.2、RC低通滤波器的截止频率
- 3.3、仿真结果-波形对比
- 四、总结
以下内容是关于模拟信号,传感器输出数字量的请上滑,输出模拟量的请放心食用!所以输出模拟量传感器的优势在哪里(我理解的输出数字量的数据是将采样的过程封装到了传感器里面,并输出数字量信号)?敲黑板:此处的响应时间并非时间常数。
一、传感器的响应时间
以温度传感器和气压传感器为例,文档中要求的动态响应如图1所示。其中温度传感器的时间常数是 τ 1 ≤ 2.5 s \tau{1} \leq 2.5 \mathrm{s} τ1≤2.5s,气压传感器的时间常数是 τ 2 ≤ 0.08 s \tau{2} \leq 0.08 \mathrm{s} τ2≤0.08s。
传感器的响应时间的定义如下:假设某信号从0上升到最大值MAX,信号一共变化了MAX,那么从0.1MAX到0.9MAX的时间即为该传感器的响应时间,如果信号是下降的同理。其中信号上升时间即时间常数τ与带宽BW的关系公式是 B W = 0.35 / τ \mathrm{BW}=0.35 / \tau BW=0.35/τ。根据公式我们可以得到此信号带宽BW的最大值,为了保证信号通过滤波器不会影响该信号响应的快慢。所以滤波器的时间常数应该 ≤ \leq ≤ τ 1 \tau{1} τ1和 ≤ \leq ≤ τ 2 \tau{2} τ2。根据公式滤波器的带宽应该 ≥ \geq ≥ 0.35 / τ 1 0.35 / \tau{1} 0.35/τ1和 ≥ \geq ≥ 0.35 / τ 2 0.35 / \tau{2} 0.35/τ2。
在示波器探头参数中,也有关于其上升时间(即时间常数)与示波器信号带宽的公式,和上面公式一致即:上升时间=0.35/带宽。其中示波器探头上升时间的定义为:从最终值的0.1上升到最终值的0.9所需要的时间。示波器的上升时间是示波器理论上可以显示的最快的瞬变的时间。
图1 传感器的动态响应时间
二、传感器响应时间与滤波器截止频率的关系
传感器响应时间与滤波器截止频率的本质关系是求信号带宽信号与上升时间的关系,信号的带宽会影响后一级滤波器的截止频率。如果信号的上升边沿很陡峭,上升时间很短,那么该信号的带宽就很宽;上升时间越短,信号的带宽越宽。
2.1、信号的带宽计算公式
通常为了提高传感器信号的准确测量,不仅需要对信号进行放大到ADC的量程范围最大化使用ADC的性能,还要对信号进行输入滤波和输出滤波,此时滤波器的截止频率和响应时间密切相关。如果某信号的上升时间不大于t,即小于等于t,那么该信号的带宽不会大于0.35/t,为了保证滤波器既可以滤除高频干扰,又可以不影响该信号的传输,所以滤波器的截止频率应该大于该信号的带宽,那么0.35/t将会是你设计滤波器时的重要参考。
上面我们已经知道了信号的最大带宽,或者说最大频率,我们以无源滤波器为例,理论分析时间常数为1的信号通过不同截止频率的滤波器后的输出会是什么样子的?首先我们关注信号的幅度变化,其次通过滤波器前后的FFT变化,以及通过滤波器前后的响应时间有无变化,因为这个是传感器的一个重要参数,我们增加的滤波电路是不能影响处理后信号的响应时间。
2.2、0.35是怎么来的
假设系统是一阶,根据RC滤波器的截止频率公式, f = 1 / 2 π R C \mathrm{f}=1 / 2 \pi \mathrm{RC} f=1/2πRC。传感器响应时间的定义:假设从0.1MAX到0.9MAX需要X个时间常数,上升时间=XRC,RC=上升时间/X,代入前面公式 f = 1 / 2 π R C \mathrm{f}=1 / 2 \pi \mathrm{RC} f=1/2πRC,那么 X / 2 π = 0.35 X / 2 \pi=0.35 X/2π=0.35, X = 0.7 π ≈ 2.2 X=0.7 \pi \approx 2.2 X=0.7π≈2.2。其中时间常数定义为从0上升到1-1/e,RC充电曲线,后面补充根据RC充电公式推倒X是不是2.2,也就是上升时间需要2.2个时间常数。充电到0.9MAX需要约2.3RC,充电到0.1MAX需要约0.1RC。公式为 0.9 = 1 − e ( − t 1 / R C ) 0.9=1-e^{\left(-t_{1} / R C\right)} 0.9=1−e(−t1/RC),所以 t 1 = ln ( 10 ) ⋅ R C t_{1}=\ln (10) \cdot R C t1=ln(10)⋅RC,可以求得t1=2.303RC,当上升到0.1MAX,公式 0.1 = 1 − e ( − t 2 / R C ) 0.1=1-e^{\left(-t_{2} / R C\right)} 0.1=1−e(−t2/RC),所以 t 2 = ln ( 10 / 9 ) ⋅ R C t_{2}=\ln (10 / 9) \cdot R C t2=ln(10/9)⋅RC,可以求得t2=0.105RC,t1-t2就是2.2RC。
2.3、RC充电时间常数
其定义为:电容器的充电时间常数,当电容上的初始电压为0时,是电容的端电压达到最大值的0.63倍时所需要的时间记为 t c t_{c} tc,通常认为时间达到5倍的充电时间常数后就认为充满了,即 t = 5 t c t=5 t_{c} t=5tc,查看图2可以看到已经充电至99%或者掉电至1%。充电时间常数的大小与电路的电阻有关,按照下式计算: t c = R C t_{c}=R C tc=RC,其中R是电阻;C是电容,下图来自百度百科-电容。
假设有电源Vu通过电阻R给电容C充电,V0为电容上的初始电压值,Vu为电容充满电后的电压值,Vt为任意时刻t时电容上的电压值,那么便可以得到如下的计算公式: V t = V 0 + ( V u − V 0 ) ⋅ [ 1 − e ( − t / R C ) ] V_{t}=\mathrm{V}_{0}+\left(V_{u}-V_{0}\right) \cdot\left[1-e^{(-t / R C)}\right] Vt=V0+(Vu−V0)⋅[1−e(−t/RC)]。当电容上的初始电压为0,则公式可以简化为 V t = V u ⋅ [ 1 − e ( − t / R C ) ] V_{t}=\mathrm{V}_{u} \cdot\left[1-e^{(-t / R C)}\right] Vt=Vu⋅[1−e(−t/RC)],此时充电时间t与电压Vt的关系如表1所示,可以认为在3~5个时间常数后就充满了。当t=RC时, V t = V u ⋅ [ 1 − e ( − 1 ) ] V_{t}=\mathrm{V}_{u} \cdot\left[1-e^{(-1)}\right] Vt=Vu⋅[1−e(−1)],其中 1 − e − 1 1-e^{-1} 1−e−1就是0.63,e≈2.7182818,大约等于2.72。

图2 电容的充放电曲线
| 充电时间t | 电压Vt |
|---|---|
| t=RC | Vt=0.63Vu |
| t=2RC | Vt=0.86Vu |
| t=3RC | Vt=0.95Vu |
| t=4RC | Vt=0.98Vu |
| t=5RC | Vt=0.99Vu |
表1 电容充电时间t时的电压Vt
三、Multisim仿真
3.1、信号的带宽
使用Multisim作为仿真软件,PULSE_VOLTAGE用来模拟传感器的输出,使用RC构造无源低通滤波器作为滤波电路(因为在放大电路的前后使用了低通滤波器作为输入和输出滤波)。其中PULSE_VOLTAGE的波形如图所示,是一个先上升后下降的三角波,上升时间和下降时间均是1ms,三角波的周期是1ms,RC无源滤波电路的截止频率满足公式: 1 / 2 π R C 1 / 2 \pi R C 1/2πRC。对于PULSE_VOLTAGE,因为上升时间和下降时间均是1ms,可以认为其时间常数等于0.8ms,那么其带宽则是437.5Hz。
图3 响应时间与滤波器的Multisim仿真
3.2、RC低通滤波器的截止频率
RC低通滤波器的截止频率满足公式 f c = 1 2 π R C f_{c}=\frac{1}{2 \pi R C} fc=2πRC1。通过改变电容值,改变滤波器的截止频率,选取电容值为10nF、100nF、1000nF,可以设置滤波器的截止频率为过高、合适、过低。
| 电容值 | 截止频率 |
|---|---|
| 10nF | 15914Hz |
| 100nF | 1591.4Hz |
| 1000nF | 159.14Hz |
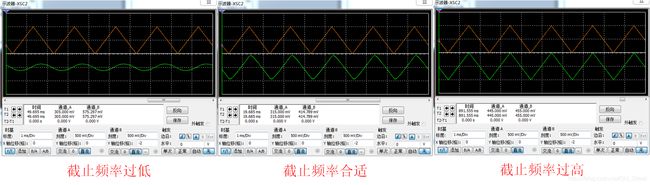
3.3、仿真结果-波形对比
图4 仿真结果
四、总结
B W = 0.35 / τ \mathrm{BW}=0.35 / \tau BW=0.35/τ是对信号处理时设计滤波器时的重要参考,但是在设计完毕后,实测信号通过滤波器后是否满足要求才是最重要的。
- 截止频率过低
如果截止频率过低,那么变化太快的信号是不能通过滤波器的,可以发现三角波几乎已经变成正弦波,并且幅度也衰减了很多。 - 截止频率过高
截止频率远大于信号带宽,信号通过滤波器几乎不会变化,但是截止频率过高就丧失了滤波器的作用,不能滤掉无效高频信号,仿真的时候为了更加真实可以增加一个高频信号源用以模拟高频噪声。 - 合适的截止频率
设置合适的截止频率,不仅可以保证通过滤波器后的信号的响应时间常数满足要求,并且可以滤掉高频噪声。因为信号的带宽BW=437.5Hz,并且截止频率是-3dB点,所以不能设置437.5Hz为滤波器的截止频率,因为幅度会衰减为原来的 1 / 2 1 / \sqrt{2} 1/2。设置滤波器的截止频率为1591.4Hz,可以保证437.5Hz处于滤波器的平坦带。输出的信号在顶部和顶部变平缓的原因是并不是理想的滤波器,从50Hz~fc,其衰减幅度是越来越大的从0dB到-3dB,通过设置坐标轴范围[红色方框所示],可以观察到[黄色圈的部分]不是垂直向下而是一个缓慢变化的曲线。
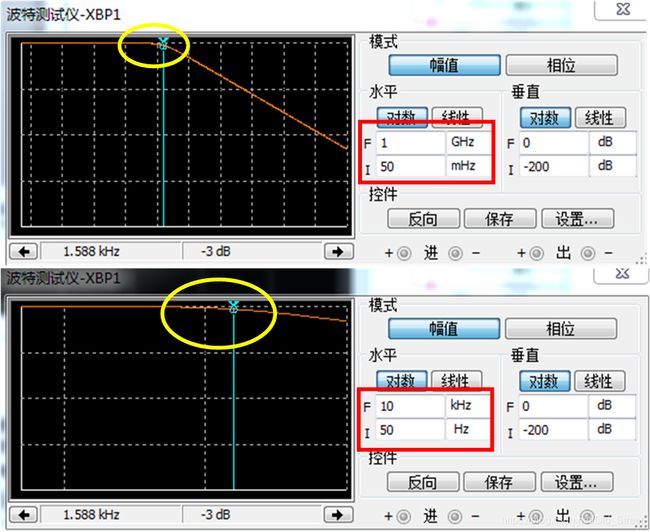
图5 滤波器的幅频特性