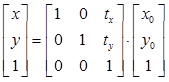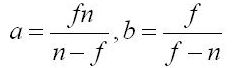Computer Vision: Algorithms and Applications（学习笔记二）--geometric transformations
2D变换
平移变换（translation）：对于2D基元的平移变换为：
其中
为2×2的单位矩阵，则公式可理解为对于坐标点
的加减变换：
为满足两端的变量的齐次性，也可写作：
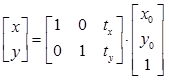
欧氏变换（Euclidean）：在平移变换的基础上加上旋转：
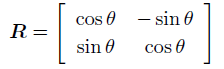
其中R维护正交矩阵，即满足
。
相似变换（similarity）：在欧氏变换的基础上加上全局尺度因子：
仿射变换（affine）：在相似变换的基础上具有两个尺度因子，在主方向和次方向具有不同的尺度因子：
投影变换（projective）：也成为透视变化或同态变化：
其中
是任意的一个3×3矩阵，而且对应的是二维变化，是齐次的，故对于不同尺度量的
是等同的，得到齐次的
需要经过正常化处理，即：
总结常用2D变换表如下：
上述变换均可用于2D平面上的坐标点，是否可以直接应用于变换直线方程，对于齐次方程
，可推导：
故上述2D变换可直接用于2D直线的齐次表达变换。
拉伸/挤压（stretch/squash）：改变图像的长宽比，一种仿射变换的受限形式，未旋转的仿射变换：
3D变换
3D坐标变换几何与2D变换的情形非常相似，如下表：
3D旋转
欧拉角（Euler angles）：旋转矩阵是由围绕三个基轴的三个旋转的乘积形成的，即
轴，旋转角为
，则三次旋转矩阵为：
乘积得到旋转矩阵为：
欧拉角是旋转三次，旋转的次序会对结果产生影响，并且会出现万向节死锁问题（http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html），不是很好用。
轴/角（axis/angle）:轴/角是将三维旋转看作绕特定的轴
旋转一次角度为
，与旋转矩阵的关系为：
则旋转矩阵可以求解：
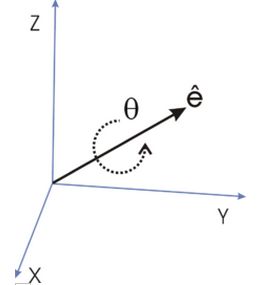
单位四元组（unit quaternions）:单位四元组与轴/角原理相同，只是将轴/角表达为一个四维的单位矢量，写作
，其中：
在选择表达方式时，一般根据应用选择。轴/角比较直观，容易理解，但是需要是动态表达，四元组没有不连续性，一般优先选择。
3D到2D投影
正交投影（orthography）：正交投影是舍弃三维坐标的
分量得到二维坐标。使用齐次坐标可以写作：
归一的正交投影（scaled orthography）：为了简化计算，将物体投影在不同的平行于图像平面的不同参考面上。
类透视投影（para-perspective）：可以理解为分两步进行，第一步是在归一化的正交投影基础上，局部参考面的投影使用平行于物体中心的视线进行投影（图中实线部分），第二步再按照正常的投影方式（相似变换）投影到最终的图像平面上。这种投影的好处是比归一化的正交投影精度高，也不需要透视投影的除法增加计算复杂性。这两步组合可看作仿射变换。
透视投影（perspective）：就是常见的透视现象，使得离摄像机近的物体投影后较大，而离摄像机较远的物体投影后较小。故可用视锥体表示：
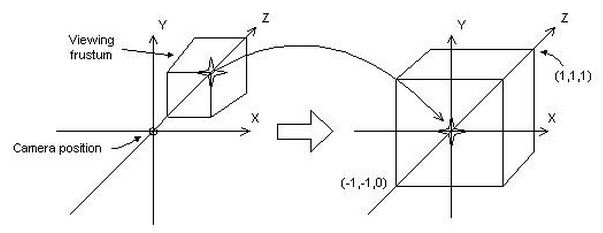
为了方便推到，一般将是锥体搬到一个统一标准的立方体中进行计算，满足
，如图所示：
此时投影到
的平面上，则依照比例关系得到点坐标为：
由于使得离摄像机近的物体投影后较大，而离摄像机较远的物体投影后较小，则最终值与 的倒数成线性关系，则表示为：
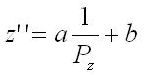
又有z的近截面Near和远截面Far范围缩小为0到1，故有公式：
解得：
又有x与z的反比参数为视角的余切值，投影平面的纵横比为Aspect，则最终投影变换公式为：
