LeetCode题解——随机刷题(一)
文章目录
-
- 146. LRU缓存机制
-
- 哈希表和双向链表
- 152. 乘积最大子数组
-
- 动态规划
- 2. 两数相加
-
- 直接遍历
- 4. 寻找两个正序数组的中位数
-
- 解法
- 5. 最长回文子串
-
- 双指针
- 11. 盛最多水的容器
-
- 双指针
- 15. 三数之和
-
- 双指针
-
- 推荐阅读
146. LRU缓存机制
146. LRU缓存机制
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果关键字 (key) 存在于缓存中,则获取关键字的值(总是正数),否则返回 -1。
写入数据 put(key, value) - 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字/值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:
你是否可以在 O(1) 时间复杂度内完成这两种操作?
示例:
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得关键字 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得关键字 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4
哈希表和双向链表
使用哈希表可以快速定位LRU里面有的节点,get时很快,使用双向链表可以很快速地插入、删除链表中的节点。
class LRUCache {
class DLinkedNode {
int key;
int value;
DLinkedNode prev;
DLinkedNode next;
public DLinkedNode() {
};
public DLinkedNode(int key, int value) {
this.key = key;
this.value = value;
}
}
private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
private int size;
private int capacity;
private DLinkedNode head, tail;
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DLinkedNode node = cache.get(key);
if (node == null) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if (node == null) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode newNode = new DLinkedNode(key, value);
// 添加进哈希表
cache.put(key, newNode);
// 添加至双向链表的头部
addToHead(newNode);
size++;
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode removeNode = removeTail();
// 删除哈希表中对应的项
cache.remove(removeNode.key);
size--;
}
} else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
node.value = value;
moveToHead(node);
}
}
private void addToHead(DLinkedNode node) {
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
private void removeNode(DLinkedNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
private void moveToHead(DLinkedNode node) {
removeNode(node);
addToHead(node);
}
private DLinkedNode removeTail() {
DLinkedNode res = tail.prev;
removeNode(res);
return res;
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/
152. 乘积最大子数组
152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
示例 1:
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
动态规划
考虑负负得正的情况。
class Solution {
public int maxProduct(int[] nums) {
int size = nums.length;
if (size == 0) {
return 0;
}
if (size == 1) {
return nums[0];
}
int ans = nums[0];
int maxValue = nums[0];
int minValue = nums[0];
for (int i = 1; i < size; i++) {
int max = maxValue, min = minValue;
maxValue = Math.max(max * nums[i], Math.max(min * nums[i], nums[i]));
minValue = Math.min(max * nums[i], Math.min(min * nums[i], nums[i]));
ans = Math.max(maxValue, ans);
}
return ans;
}
}
2. 两数相加
2. 两数相加
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807
直接遍历
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode dummyHead = new ListNode(0);
ListNode p = l1, q = l2, curr = dummyHead;
int carry = 0;
while (p != null || q != null) {
int x = (p != null) ? p.val : 0;
int y = (q != null) ? q.val : 0;
int sum = carry + x + y;
carry = sum / 10;
curr.next = new ListNode(sum % 10);
curr = curr.next;
if (p != null) {
p = p.next;
}
if (q != null) {
q = q.next;
}
}
if (carry > 0) {
curr.next = new ListNode(carry);
}
return dummyHead.next;
}
}
4. 寻找两个正序数组的中位数
4. 寻找两个正序数组的中位数
给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。
请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
解法
详解见leetcode
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int n = nums1.length;
int m = nums2.length;
int left = (n + m + 1) / 2;
int right = (n + m + 2) / 2;
return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;
}
private int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
int len1 = end1 - start1 + 1;
int len2 = end2 - start2 + 1;
if (len1 > len2) {
return getKth(nums2, start2, end2, nums1, start1, end1, k);
}
if (len1 == 0) {
return nums2[start2 + k - 1];
}
if (k == 1) {
return Math.min(nums1[start1], nums2[start2]);
}
int i = start1 + Math.min(len1, k / 2) - 1;
int j = start2 + Math.min(len2, k / 2) - 1;
if (nums1[i] > nums2[j]) {
return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
} else {
return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
}
}
}
5. 最长回文子串
5. 最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
示例 2:
输入: “cbbd”
输出: “bb”
双指针
遍历每一个索引,以这个索引为中心,利用“回文串”中心对称的特点,往两边扩散,看最多能扩散多远。
回文串在长度为奇数和偶数的时候,“回文中心”的形式是不一样的。
-
奇数回文串的“中心”是一个具体的字符,例如:回文串 “aba” 的中心是字符 “b”;
-
偶数回文串的“中心”是位于中间的两个字符的“空隙”,例如:回文串串 “abba” 的中心是两个 “b” 中间的那个“空隙”。
class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
String res = s.substring(0, 1);
// 中心位置枚举到 len - 2 即可
for (int i = 0; i < len - 1; i++) {
String oddStr = centerSpread(s, i, i);
String evenStr = centerSpread(s, i, i + 1);
String maxLenStr = oddStr.length() > evenStr.length() ? oddStr : evenStr;
if (maxLenStr.length() > maxLen) {
maxLen = maxLenStr.length();
res = maxLenStr;
}
}
return res;
}
private String centerSpread(String s, int left, int right) {
// left = right 的时候,此时回文中心是一个字符,回文串的长度是奇数
// right = left + 1 的时候,此时回文中心是一个空隙,回文串的长度是偶数
int len = s.length();
int i = left;
int j = right;
while (i >= 0 && j < len) {
if (s.charAt(i) == s.charAt(j)) {
i--;
j++;
} else {
break;
}
}
// 这里要小心,跳出 while 循环时,恰好满足 s.charAt(i) != s.charAt(j),因此不能取 i,不能取 j
return s.substring(i + 1, j);
}
}
11. 盛最多水的容器
11. 盛最多水的容器
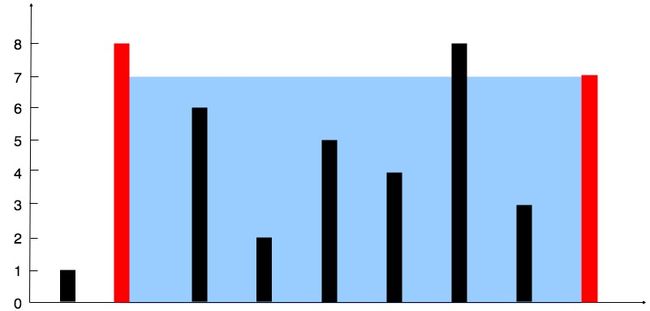
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
双指针
首尾各一个指针,每次向内移动短板,可以得到最大值。
class Solution {
public int maxArea(int[] height) {
int i = 0, j = height.length - 1, res = 0;
while (i < j) {
res = height[i] < height[j] ? Math.max(res, (j - i) * height[i++]) : Math.max(res, (j - i) * height[j--]);
}
return res;
}
}
15. 三数之和
15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
双指针
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
int len = nums.length;
for (int i = 0; i < len; i++) {
// 后面的元素肯定不满足要求,都是大于0的
if (nums[i] > 0) {
return res;
}
// 遇到重复的跳过
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int cur = nums[i];
int left = i + 1, right = len - 1;
while (left < right) {
int tmp = cur + nums[left] + nums[right];
if (tmp == 0) {
List<Integer> list = Arrays.asList(cur, nums[left], nums[right]);
res.add(list);
// 剔除重复的
while (left < right && nums[left + 1] == nums[left]) {
++left;
}
while (left < right && nums[right - 1] == nums[right]) {
--right;
}
// 同时移动left、right
++left;
--right;
} else if (tmp < 0) {
// 说明left太小,left前进
++left;
} else {
--right;
}
}
}
return res;
}
}
推荐阅读
- 剑指offer精品题解
- 机器学习资料汇总
- 吴恩达《机器学习》视频、作业、源码
- 106页《Python进阶》中文版正式发布
- 李航《统计学习方法》第二版完整课件
- 机器学习数学全书,1900页PDF下载
欢迎关注我的公众号呦,率先更新内容,并且后续还有一些源码级的免费教程推出。
![]()