NLP基础之词向量（Word2Vector）

NLP基础之词向量（Word2Vector）

0. 前言

与图像或相比，语言是一种经过人类智力处理后的、更为抽象的数据对象，因此nlp相比cv相比有许多独特之处，研究起来也比较复杂，其中词的表征方式就是一个重要方面。

1. one-hot向量

词（Word）最简单粗暴的一种表征方式（representation）就是one-hot vector。记$V$为词库，$|V|$为词库大小，则每个词可以表征为一个$R^{|V|\times 1}$的向量，其中第$k$维为1，其他维为0 ，$k$是该词在词库中的位置。这种方式的缺点在于：

• 维数可能会很大，词向量会很稀疏
• 无法衡量词与词之间的相似性（任何两个词之间的内积或者余弦相似度都为0）
  因此，我们自然而然地想能否将词向量的空间$R|V|$降维成一个子空间，并且这个子空间可以表征出词与词之间的关系。

2. SVD分解

先遍历一个大的文档集，统计每两个词是否配对出现。例如，设文档集里面的句子为如下：

1. I enjoy flying.
2. I like NLP.
3. I like deep learning.
   则可以都得到这样的共现矩阵(Co-occurrence Matrix)：
   

对$X$进行SVD分解：
$$X=U\Sigma V^T\text{\hspace{1em}(2,1)}$$
假设选取前$k$个奇异值对应主要成分，则应该选择$U_{1:|V|,1:k}$作为降维后的词嵌入矩阵，这样就得到了词库中每个词的$k$维表征。
这种方法的缺点是：

• 随着新词的引入，共现矩阵的大小会经常变化
• 共现矩阵很高维，而且很稀疏
• SVD分解需要很大的时间开销（约$O(n^3)$）
• SVD的可解释性较差

3. Word2Vec

前面提到的方法需要存储和计算整个语料库的所有信息，而Word2Vec通过上下文来预测词的概率，用迭代学习参数的方法，可以降低复杂度。它包含两种算法：continuous baf-of-words(CBOW)和skip-gram，两种训练方法：负采样和层级softmax。

3.1. 语言模型——n-gram

用$P({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)$表示一个具有n个词的序列（句子）的概率。Unigram模型假设每个词之间都是相互独立的，也即
$$P({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)=\prod _{i=1}^{n}P({\omega }_i)\text{\hspace{1em}(3-1)}$$
Bigram模型假设每个词只与它前面的词有关：
$$P({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)=\prod _{i=1}^{n}P({\omega }_i|{\omega }_{i-1})\text{\hspace{1em}(3-2)}$$
类似地可以得到n-gram的表达式。一般用CBOW或者Skip-gram方法来学习出一个句子的概率。
简而言之，CBOW的目的是通过上下文来预测中心词，而Skip-gram是通过中心词来预测上下文的分布。它们的作用都是将one-hot表示的词“嵌入”到一个低维空间中，这个方法也叫“词嵌入”（Word Embedding）

3.2. Continuous Bag of Words Model(CBOW)

先考虑bigram的情形，也即利用一个词预测下一个词。此时，输入词是语境词（context word）$w_I$，输出词是目标词$w_O$。
记输入词的one-hot向量为$x,x_k=1,x_{k^{\prime }}=0for{k}^{\prime }\ne k$，输出词的one-hot向量为$y$。它们的维度都是$|V|$，非常大。我们希望将每个词的one-hot向量映射到一个较低的维度$N$上（同时还能较好地表达词的含义以及词与词之间的关系）。为此，我们在输入词和输出词之间增加一个$N$个节点的隐藏层，输入层到隐藏层的权重矩阵记为$W_{V\times N}$，称之为输入层矩阵，隐藏层到输出层的权重矩阵记为$W_{N\times V}^{\prime }$，称之为输出词矩阵。我们就是希望通过一系列训练数据和上述模型结构学习到输入词矩阵和输出词矩阵。
一般我们用的词向量是输入层矩阵，输出层矩阵代表了上下文词与目标词之间的关系。最开始的时候并不是这么做，最开始为了降低输出端反向传播的计算复杂度，用的是hierarchical softmax，输出端是二叉树结构，输出端参数是二叉树中每个节点的向量，输出向量是和二叉树的节点一一对应的，跟word根本对应不上来，这种情况你只能利用输入端的词向量。
bigram的CBOW模型可以表示为如下的一个两层神经网络结构：

输入层到隐藏层的矩阵运算为：
$$h=W^{T}x=W_{(k,:)}^T:=v_{w_I}\text{\hspace{1em}(3-3)}$$
$W$的每一行$v_w$代表了某个词的输入词向量（第i行代表第i个词的输入词向量），输入层h其实就是把$W$的第$k$层复制过来了，它代表了输入词$w_I$的输入词向量。这个地方隐含了输入词的激活函数是线性的且不对该层的输入做任何改变。
隐藏层到输出层可以表示为：
$$U=W^{\prime T}h\text{\hspace{1em}(3-4)}$$
其中$U$的每一行$u_j=v_{w_j}^{\prime T}h$，$v_{w_j}^{\prime T}$代表了输出词矩阵$W^{\prime }$的第$j$列。再对$Z$进行一个softmax变换，就可以将其每一维都映射到$[0,1]$之间，用来代表输出层某一维不为零的概率，这样就可以与输出词的真实one-hot向量进行比较（计算loss function）。输出层第$j$个单元的值可以表示为：
$$\begin{array}{rl}p(w_j|w_I)=y_j& =\frac{exp(u_j)}{{\sum }_{i=1}^{|V|}exp(u_i)}\\ & =\frac{exp(v_{w_j}^{\prime T}{v}_{w_I})}{{\sum }_{i=1}^{|V|}exp(v_{w_j}^{\prime T}{v}_{w_I})}\end{array}\text{\hspace{1em}(3-5)}$$
上式代表的是输出词（目标词）$w_O$第$j$维不为零的概率。假设实际的目标词$w_O$的第$j^{\ast }$维不为零（为1），则该神经网络的优化目标为最大化如下式子：
$$\begin{array}{rl}maxp(w_O|w_I)& =max{y}_{j^{\ast }}\\ & =maxlog{y}_{j^{\ast }}\\ & =max\left(u_{j_{\ast }}-log\sum _{i=1}^{|V|}exp(u_i)\right)\end{array}\text{\hspace{1em}(3-6)}$$

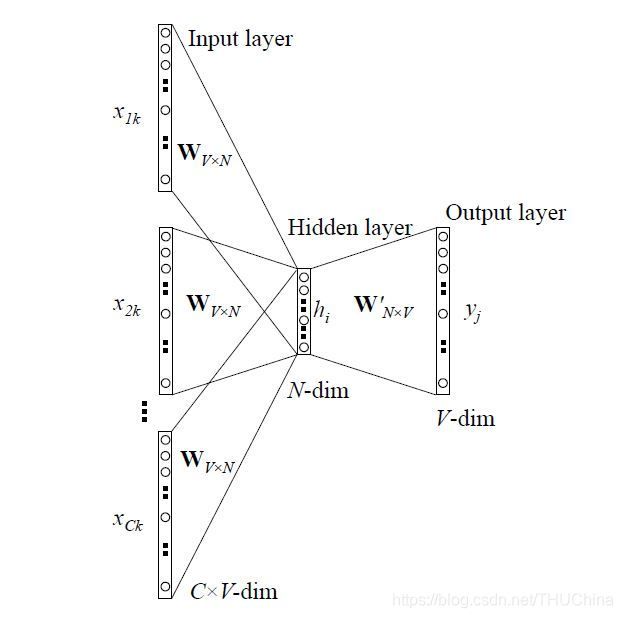
当利用多个输入词来预测一个目标词时，架构与上面类似，区别在于隐藏层的计算方式是全虫矩阵乘以输入词的one-hot向量的平均值：
$$h=\frac{1}{C}{W}^T(x_1+x_2+\cdots +x_C)\text{\hspace{1em}(3-7)}$$

3.3. Skip-Gram Model

skip-gram模型是CBOW模型的反向过程：利用一个词来预测它的上下文。记输入词为$x$，隐藏层为$h$，输入层到隐藏层的权重矩阵为$W$，输入层到隐藏层可以表示为：
$$h=W^{T}x=W_{(k,:)}^T:=v_{w_I}\text{\hspace{1em}(3-8)}$$
其中$v_{w_I}$表示代表了输入词$w_I$的输入词向量。假设上下文的词的个数为C，与CBOW不同的地方在于，隐藏层映射到输出层时，输出层有C组size为$|V|$的向量，对应每个上下文词的预测输出。
$$U_c=W^{\prime T}h\text{\hspace{1em}(3-9)}$$

假设第$c$个上下文词的实际值是$w_{O,c}$，则输出层第$c$个预测词等于实际词的概率为：
$$\begin{array}{rlr}p(w_{c,j}=w_{O,c}|w_I)& =y_{c,j}& \\ & =\frac{exp(u_{c,j})}{{\sum }_{i=1}^{|V|}exp(u_i)}& \\ & =\frac{exp(v_{w_j}^{\prime T}{v}_{w_I})}{{\sum }_{i=1}^{|V|}exp(v_{w_j}^{\prime T}{v}_{w_I})}& \end{array}\text{\hspace{1em}(3-10)}$$
loss function可以表示为：
$$\begin{array}{rl}Loss& =-logp(w_{O,1},p(w_{O,2},\cdots ,p(w_{O,C}|w_I)\\ & =-log\prod \frac{exp(u_{c,j_c^{\ast }})}{{\sum }_{i=1}^{|V|}exp(u_i)}\\ & =-\sum _{c=1}^C{u}_{j_c^{\ast }}+C\cdot log\sum _{i=1}^{|V|}exp(u_i)\end{array}\text{\hspace{1em}(3-11)}$$