数据结构入门系列——串和数组

串

1.若串s=“software”，其子串的个数是（37）。
总的子串个数=8+7+…+2+1+1=(8+1)×8/2+1=37个
n*(n+1)/2+1
2.串相等的充要条件：字符串长度相等，两字符串中相同位置字符相同

顺序串

定义

类似顺序表

#include
using namespace std;
#define maxsize 100
typedef struct
{
     
	char data[maxsize];
	int length;
}SqString;

基本算法

较难想的：

/*查找子串位置运算算法*/
/*返回顺序串t在顺序串s中的位置。难度颇大*/
int Index(SqString s, SqString t)
{
     
	int i = 0, j = 0;	//i和j分别扫描主串s和子串t
	while (i < s.length && j < t.length)
	{
     
		if (s.data[i] == t.data[j])
		{
     
			i++;		//对应字符相同时,继续比较下一对字符
			j++;
		}
		else		//否则,主串指针回溯重新开始下一次匹配
		{
     
			i = i - j + 1;
			j = 0;
		}
	}
	if (j >= t.length)
		return i - t.length + 1;	//返回第一个字符的位置
	else
		return 0;		//返回0

}
//子串插入运算算法
int InsStr(SqString &s, int i, SqString t)
{
     
	int j;
	if (i<1 || i>s.length + 1)
		return 0;			//位置参数错误返回0
	else
	{
     
		for (j = s.length - 1; j >= i - 1; j--)
			//将s.data[i-1..s.length-1]后移t.length个位置
			s.data[j + t.length] = s.data[j];
		for (j = 0; j < t.length; j++)	//插入子串t
			s.data[i + j - 1] = t.data[j];
		s.length = s.length + t.length;	//修改s串长度
		return 1;			//成功插入返回1
	}
}

/*将字符串赋值给串*/
void Assign(SqString &st, char str[])
{
     
	int i = 0;
	while (str[i] != '\0')  //C++用字符数组存储串，以 \0 标识结束。
	{
     
		st.data[i] = str[i];
		i++;
	}
	st.length = i;
}
void DestroyStr(SqString st)
{
     }
/*将一个串t复制给另一个串s*/
void StrCopy(SqString &s, SqString t)
{
     
	int i;
	for (i = 0; i < t.length; i++)
	{
     
		s.data[i] = t.data[i];
	}
	s.length = i;
}
/*判断串相等*/
int StrEqual(SqString s, SqString t)
{
     
	int i = 0;
	if (s.length != t.length)	       //串长不同时返回0
		return(0);
	else
	{
     
		for (i = 0; i < s.length; i++)
			if (s.data[i] != t.data[i])   //有对应字符不同时返回0
				return 0;
		return 1;
	}
}
/*串连接运算算法*/
SqString Concat(SqString s, SqString t)
{
     
	SqString r;
	int i, j;
	for (i = 0; i < s.length; i++)		//将s复制到r
		r.data[i] = s.data[i];
	for (j = 0; j < t.length; j++)		//将t复制到r
		r.data[s.length + j] = t.data[j];
	r.length = i + j;
	return r;				//返回r
}

/*求子串运算算法*/
/*返回顺序串s的第i个位置开始的j个字符组成的顺序串，当参数错误时返回一个空顺序串。 */
SqString SubStr(SqString s, int i, int j)
{
     
	SqString t;
	int k;
	if (i<1 || i>s.length || j<1 || i + j>s.length + 1)
		t.length = 0;	//参数错误时返回空串
	else
	{
     
		for (k = i - 1; k < i + j; k++)
			t.data[k - i + 1] = s.data[k];
		t.length = j;
	}
	return t;
}
/*查找子串位置运算算法*/
/*返回顺序串t在顺序串s中的位置。难度颇大*/
int Index(SqString s, SqString t)
{
     
	int i = 0, j = 0;	//i和j分别扫描主串s和子串t
	while (i < s.length && j < t.length)
	{
     
		if (s.data[i] == t.data[j])
		{
     
			i++;		//对应字符相同时,继续比较下一对字符
			j++;
		}
		else		//否则,主串指针回溯重新开始下一次匹配
		{
     
			i = i - j + 1;
			j = 0;
		}
	}
	if (j >= t.length)
		return i - t.length + 1;	//返回第一个字符的位置
	else
		return 0;		//返回0

}
//子串插入运算算法
int InsStr(SqString &s, int i, SqString t)
{
     
	int j;
	if (i<1 || i>s.length + 1)
		return 0;			//位置参数错误返回0
	else
	{
     
		for (j = s.length - 1; j >= i - 1; j--)
			//将s.data[i-1..s.length-1]后移t.length个位置
			s.data[j + t.length] = s.data[j];
		for (j = 0; j < t.length; j++)	//插入子串t
			s.data[i + j - 1] = t.data[j];
		s.length = s.length + t.length;	//修改s串长度
		return 1;			//成功插入返回1
	}
}
//子串删除运算算法
int DelStr(SqString &s, int i, int j)
{
     
	int k;
	if (i<1 || i>s.length || j<1 || i + j>s.length + 1)
		return 0;		//位置参数值错误
	else
	{
     
		for (k = i + j - 1; k < s.length; k++)
			//将s的第i+j位置之后的字符前移j位
			s.data[k - j] = s.data[k];
		s.length = s.length - j;	//修改s的长度
		return 1;   //成功删除返回1
	}
}
//子串替换运算算法
SqString RepStrAll(SqString s, SqString s1, SqString s2)
{
     
	int i;
	i = Index(s, s1);
	while (i > 0)
	{
     
		DelStr(s, i, s1.length);	//删除子串s1
		InsStr(s, i, s2);		//插入子串s2
		i = Index(s, s1);
	}
	return s;
}
void DispStr(SqString s)
{
     
	int i;
	for (i = 0; i < s.length; i++)
		printf("%c", s.data[i]);
	printf("\n");
}

链串

定义

typedef struct node
{
     
	char data;		  //存放字符
	struct node *next;	  //指针域
} LinkString;		  //链串结点类型

基本算法

//赋值
void Assign(LinkString *&s, char str[])
{
     
	int i = 0;
	LinkString *p, *tc;
	s = (LinkString *)malloc(sizeof(LinkString));
	tc = s;			 //tc指向s串的尾结点
	while (str[i] != '\0')
	{
     
		p = (LinkString *)malloc(sizeof(LinkString));
		p->data = str[i];
		tc->next = p; tc = p;
		i++;
	}
	tc->next = NULL;		//尾结点的next置NULL
}
//
void DestroyList(LinkString *&s)
{
     
	LinkString *pre = s, *p = pre->next;
	while (p != NULL)
	{
     
		free(pre);
		pre = p; p = p->next;   //pre、p同步后移
	}
	free(pre);
}

数组

数组的存储结构

对于$A_{m\ast n}$数组：
1.按行优先：
对于元素$a_{i,j}$有：
$LOC(a_{i,j})=LOC(a_{0,0})+(i\ast n+j)\ast k$¹

2.按列优先：
对于元素$a_{i,j}$有：
$LOC(a_{i,j})=LOC(a_{0,0})+(j\ast m+i)\ast k$

数组转置算法

void TransMat(int A[][MAX], int B[][MAX],int m,int n)
{
       int i,j;
   for (i=0;i<m;i++)
	for (j=0;j<n;j++)
	　　B[j][i]=A[i][j];
}

特殊矩阵压缩

1.对称矩阵

2.对称矩阵b=1

当b=1时：
$k=2i+j$。

3.稀疏矩阵

稀疏矩阵的三元组表示

定义：

#define M 10
#define N 10
#define MaxSize  100		//矩阵中非零元素的最多个数
typedef struct
{
     
	int r;			//行号
	int c;			//列号
	int d;			//元素值为ElemType类型
} TupNode;			//三元组定义
typedef struct
{
     
	int rows;			//行数
	int cols;			//列数
	int nums;			//非零元素个数
	TupNode data[MaxSize];
} TSMatrix;			//三元组顺序表定义

由于三元组压缩使得矩阵失去随机存取的特性，导致读取的算法较为复杂。

/*三元组元素赋值*/
int Value(TSMatrix &t, int x, int i, int j)
{
     
	int k = 0, k1;
	if (i >= t.rows || j >= t.cols)  return 0;	//参数错误
	while (k<t.nums && i>t.data[k].r) k++;	//查找行

	while (k<t.nums && i == t.data[k].r && j>t.data[k].c)
		k++; 					//查找列

	if (t.data[k].r == i && t.data[k].c == j)	//存在元素
		t.data[k].d = x;
	else			//不存在这样的元素时插入一个元素
	{
     
		for (k1 = t.nums - 1; k1 >= k; k1--)
		{
     
			t.data[k1 + 1].r = t.data[k1].r;
			t.data[k1 + 1].c = t.data[k1].c;
			t.data[k1 + 1].d = t.data[k1].d;
		}
		t.data[k].r = i; t.data[k].c = j;
		t.data[k].d = x; t.nums++;
	}
	return 1;			//成功时返回1
}
/*将指定位置的元素值赋给变量*/
int Assign(TSMatrix t, int &x, int i, int j)
{
     
	int k = 0;
	if (i >= t.rows || j >= t.cols)
		return 0;				//参数错误
	while (k<t.nums && i>t.data[k].r) k++;	//查找行
	while (k<t.nums && i == t.data[k].r && j>t.data[k].c)
		k++;					//查找列
	if (t.data[k].r == i && t.data[k].c == j)
		x = t.data[k].d;
	else
		x = 0;		//在三元组中没有找到表示是零元素
	return 1;		//成功时返回1
}

其他代码：

/*从一个二维稀疏矩阵创建其三元组表示*/
void CreatMat(TSMatrix &t, int A[M][N])
{
     
	int i, j;
	t.rows = M; t.cols = N; t.nums = 0;
	for (i = 0; i < M; i++)
	{
     
		for (j = 0; j < N; j++)
			if (A[i][j] != 0) 	//只存储非零元素
			{
     
				t.data[t.nums].r = i;
				t.data[t.nums].c = j;
				t.data[t.nums].d = A[i][j];
				t.nums++;
			}
	}
}
/*三元组元素赋值*/
int Value(TSMatrix &t, int x, int i, int j)
{
     
	int k = 0, k1;
	if (i >= t.rows || j >= t.cols)  return 0;	//参数错误
	while (k<t.nums && i>t.data[k].r) k++;	//查找行

	while (k<t.nums && i == t.data[k].r && j>t.data[k].c)
		k++; 					//查找列

	if (t.data[k].r == i && t.data[k].c == j)	//存在元素
		t.data[k].d = x;
	else			//不存在这样的元素时插入一个元素
	{
     
		for (k1 = t.nums - 1; k1 >= k; k1--)
		{
     
			t.data[k1 + 1].r = t.data[k1].r;
			t.data[k1 + 1].c = t.data[k1].c;
			t.data[k1 + 1].d = t.data[k1].d;
		}
		t.data[k].r = i; t.data[k].c = j;
		t.data[k].d = x; t.nums++;
	}
	return 1;			//成功时返回1
}
/*将指定位置的元素值赋给变量*/
int Assign(TSMatrix t, int &x, int i, int j)
{
     
	int k = 0;
	if (i >= t.rows || j >= t.cols)
		return 0;				//参数错误
	while (k<t.nums && i>t.data[k].r) k++;	//查找行
	while (k<t.nums && i == t.data[k].r && j>t.data[k].c)
		k++;					//查找列
	if (t.data[k].r == i && t.data[k].c == j)
		x = t.data[k].d;
	else
		x = 0;		//在三元组中没有找到表示是零元素
	return 1;		//成功时返回1
}
void DispMat(TSMatrix t)
{
     
	int i;
	if (t.nums <= 0)			//没有非零元素时返回
		return;
	cout << t.rows << '.' << t.cols << ':' << t.nums << endl;
	cout << "------------------\n";
	for (i = 0; i < t.nums; i++)
		cout << t.data[i].r << '.' << t.data[i].c << ':' << t.data[i].d << endl;
}

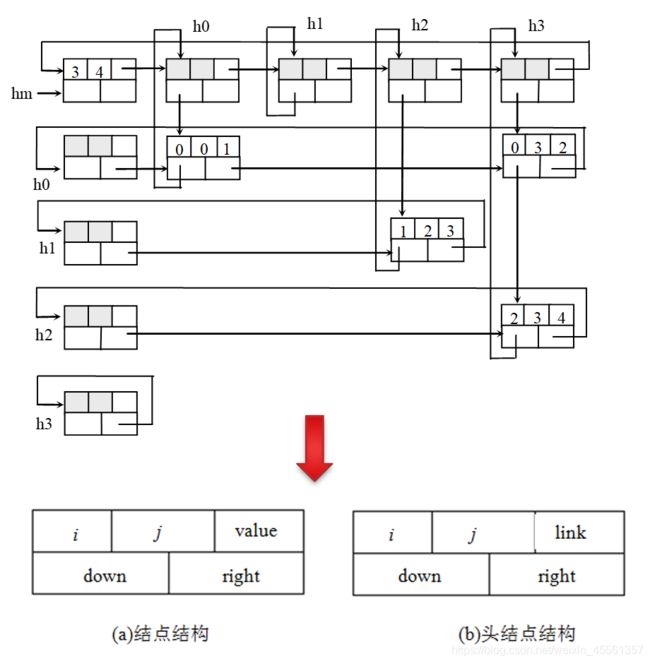
稀疏矩阵的十字链表表示

定义：

#define M 3			  //矩阵行数
#define N 4			  //矩阵列数
#define Max ((M)>(N)?(M):(N))	  //矩阵行列中较大者
typedef struct mtxn
{
     
	int i;			  //行号
	int j;			  //列号
	struct mtxn *right, *down;	  //向右和向下的指针
	union
	{
     
		ElemType value;		  //存放非零元素值
		struct mtxn *link;
	} tag;
} MatNode;			  //十字链表类型定义

---

1. 每个元素存储单元 ↩︎