2020年中国大学生数学建模竞赛备赛(六)
3.3 约束极值问题的求解
3.3.1 二次规划
定义要领:1、是非线性规划;2、目标函数是二次函数;3、约束条件全是线性。
这种规划才是二次规划。
模型表示
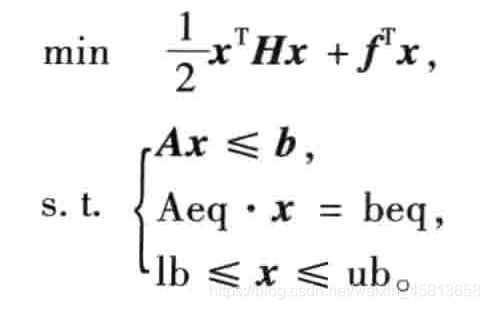
式子中, H H H是实对称矩阵; f , b , b e q , l b , u b f,b,beq,lb,ub f,b,beq,lb,ub是列向量; A , A e q A,Aeq A,Aeq是相应维数的矩阵。
[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options);
3.2 罚函数法
所谓罚函数法(又名乘子法),就是将非线性规划问题的求解转化为一系列无约束极值问题的求解,也称为序列无约束最小化技术。表示为 F ( x , M ) F(x,M) F(x,M),其中 M M M为足够大的数,称为惩罚项。
基本思想:利用问题中的约束函数做出适当的罚函数,构造出带参数的增广目标函数,把问题转化为无约束非线性规划问题。
两种方法:外罚函数法和内罚函数法。
外部罚函数法是从非可行解出发逐渐移动到可行区域的方法。
内部罚函数法也称为障碍罚函数法,这种方法是在可行域内部进行搜索,约束边界起到类似围墙的作用,如果当前解远离约束边界时,则罚函数值是非常小的,否则罚函数值接近无穷大的方法。
在进化计算中,研究者多选择外部罚函数法。原因主要是该方法不需要提供初始可行解。
需要提供初始可行解则是内部罚函数法的主要缺点。由于进化算法应用到实际问题中可能存在搜索可行解就是NP难问题,因此这个缺点是非常致命的。
罚函数法最难的地方在于罚因子的选取。罚因子应该往小的方向选择,但是又不能过小,否则会让可行解落在可行域之外,而且当罚函数项过小时,目标函数中的罚函数项则会被忽略,使得最优搜索浪费过多时间在非可行域内;如果罚因子很大并且最优解在可行域边界,进化算法将很快被推进到可行域以内,这将不能返回到非可行域的边界。在搜索过程开始的时候,一个较大的罚因子将会阻碍非可行域的搜索。
值得注意的是,罚函数对可行域的连通性也有一定的要求,如果是非连通的可行域,除非可行域之间特别地接近,否则不会搜索到全部可行域内的可行解。
下面是外罚函数法的简介:


例题:
//定义增广目标函数
function g=test1(x)
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);
end
//用求矩阵极大值和极小值函数定义增广函数
function g=test2(x)
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*sum(min([x';zeros(1,2)]))-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);
end
//也可以修改增广函数的定义
function g=test3(x)
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*min(min(x),0)-M*min(x(1)^2-x(2),0)+M*(-x(1)-x(2)^2+2)^2;
end
[x,y]=fminunc('test3',rand(2,1));
注:
(1)所谓实时算法,是指时间复杂度较低的计算方法。
(2)如果非线性规划问题要求实时算法,可以使用罚函数方法,但精度较低;
(3)如果不要求实时算法,但计算精度要求高,则使用其它的方法。
参考文献
[1]司守奎,孙玺菁. 数学建模算法与应用. 北京:国防工业出版社,2011.