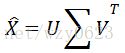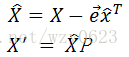MADlib——基于SQL的数据挖掘解决方案(10)——数据探索之主成分分析
数据挖掘中经常会遇到多个变量的问题,而且在多数情况下,多个变量之间常常存在一定的相关性。例如,网站的“浏览量”和“访客数”往往具有较强的相关关系,而电商应用中的“下单数”和“成交数”也具有较强的相关关系。这里的相关关系可以直观理解为当浏览量较高(或较低)时,应该很大程度上认为访客数也较高(或较低)。在这个简单的例子中只有两个变量,当变量个数较多且变量之间存在复杂关系时,会显著增加分析问题的复杂性。主成分分析方法可以将多个变量综合为少数几个代表性变量,使这些变量既能够代表原始变量的绝大多数信息又互不相关,这种方法有助于对问题的分析和建模。
MADlib提供了两组主成分分析函数:训练函数与投影函数。训练函数以原始数据为输入,输出主成分。投影函数将原始数据投影到主成分上,实现线性无关降维,输出降维后的数据矩阵。本篇介绍MADlib主成分分析模型对应的函数,并以一个示例说明如何利用这些函数解决数据的去相关性和降维问题。
一、主成分分析简介
1. 基本思想
主成分分析(Principal Component Analysis,PCA)采取一种数学降维的方法,其所要做的就是设法将原来众多具有一定相关性的变量,重新组合为一组新的相互无关的综合变量来代替原来的变量。通常,数学上的处理方法就是将原来的变量做线性组合,作为新的综合变量,转换后的变量叫主成分。变换的定义方法是用F1(选取的第一个线性组合,即第一个综合指标)的方差来表达,即Var(F1)越大,表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2即选第二个线性组合,为了有效地反映原始信息,F1已有的信息不需要再出现在F2中,用数学语言表达就是要求Cov(F1, F2)=0,称F2为第二主成分,依此类推可以构造出第三、第四......第P个主成分。Cov表示统计学中的协方差。
PCA的目标是找出一个更好地捕获数据变异性的、新的变量集合。更明确地说,所选择的第一个变量要尽可能多地捕获数据的变异性。第二个变量与第一个正交,并且尽可能多地捕获剩余的变异性,如此下去。
PCA具有一些引人注目的特性。首先,它趋向于确定数据中最强的模式。因此,PCA可以用作模式发现技术。其次,数据的大部分变异性通常都可以被整个变量集合的一小部分新变量所捕获。这样,使用PCA进行降维可以产生相对低维的数据,使得我们有可能使用在高维数据上不太有效的技术。再次,由于通常数据中的噪声比模式弱,降维可以去掉许多噪声。这有利于应用数据挖掘和其它数据分析算法。
2. 数学细节
统计学中通过计算数据的协方差矩阵S汇总多元数据集(例如,具有多个连续属性的数据)的变异性。数据的变异性可看作是对不同数值间的差异性的度量。
给定一个m×n的数据矩阵D,其m个行是数据对象,其n个列是属性。D的协方差矩阵是矩阵S,其元素![]() 定义为:
定义为:
![]()
换言之,![]() 是数据的第 i 和第 j 个属性(列)的协方差。设x为第 i 个属性对应的列向量,y为第 j 个属性对应的列向量,则:
是数据的第 i 和第 j 个属性(列)的协方差。设x为第 i 个属性对应的列向量,y为第 j 个属性对应的列向量,则:
两个属性的协方差度量两个属性一起变换的程度。如果i=j(即x=y,两个属性相同),则协方差就是该属性的方差。如果数据矩阵D经过预处理,使得每个属性的均值都是0,则![]() 。
。
PCA的目标是找到一个满足如下性质的数据变换:
(1) 每对不同的新属性的协方差为0。
(2) 属性按照每个属性捕获的数据方差的多少排序。
(3) 第一个属性捕获尽可能多的数据方差。
(4) 在满足正交性的前提下,每个后继属性捕获尽可能多的剩余方差。
3. 计算步骤
下面简单介绍一下PCA转换的典型步骤。
(1) 对原始数据进行标准化处理
假设样本观测数据矩阵为:
那么可以按照如下方法对原始数据进行标准化处理:
(2) 计算样本相关系数矩阵
为方便,假定原始数据标准化后仍用 X 表示,则经标准化处理后数据的相关系数为:
(3) 计算相关矩阵R的特征值![]() 和相应的特征向量:
和相应的特征向量:
(4) 选择重要的主成分,并写出主成分表达式
主成分分析可以得到 p 个主成分,但是,由于各个主成分的方差是递减的,包含的信息量也是递减的,所以实际分析时,一般不是选取 p 个主成分,而是根据各个主成分累计贡献率的大小选取前 k 个主成分,这里的贡献率是指某个主成分的方差占全部方差的比重,实际也就是某个特征值占全部特征值合计的比重,即:
贡献率越大,说明该主成分所包含的原始变量的信息越强。主成分个数 k 的选取,主要根据主成分的累计贡献率来决定,一般要求累计贡献率达到85%以上,这样才能保证综合变量能包括原始变量的绝大多数信息。
另外,在实际应用中,选择了重要的主成分后,还要注意对主成分实际含义的解释。主成分分析中一个很关键的问题是如何给主成分赋予新的意义,给出合理的解释。一般而言,这个解释是根据主成分表达式的系数结合定性分析来进行的。主成分是原来变量的线性组合,在这个线性组合中各变量的系数有大有小,有正有负,有的大小相当,因而不能简单地认为这个主成分是某个原变量的作用,线性组合中各变量系数的绝对值大者表明该主成分主要综合了绝对值大的变量,有几个变量系数大小相当时,应认为这一主成分是这几个变量的总和,这几个变量综合在一起应赋予怎样的实际意义,就要结合具体的实际问题和专业,给出恰当的解释,进而才能达到深刻分析的目的。
(5) 计算主成分得分
根据标准化的原始数据,按照各个样品,分别代入主成分表达式,就可以得到各主成分下的各个样品的新数据,即为主成分得分。具体形式如下:
其中![]() 。
。
(6) 依据主成分得分数据,进一步对问题进行后续的分析和建模
后续分析和建模常见的形式有主成分回归、变量子集合的选择、综合评价等。
4. PCA转换的性质
设D为原数据矩阵,D' 是经过PCA转换后的新数据矩阵,则:
- 每个新变量都是原变量的线性组合。更明确地说,第i个变量的线性组合权重是第i个特征向量的分量。第i个新变量的方差是
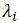 。
。 - 原变量的方差和等于新变量的方差和。
- 新变量称作主成分,也就是说,第一个新变量是第一个主成分,第二个新变量是第二个主成分,如此下去。
与最大特征值相关联的特征向量指示数据具有最大方差的方向。换句话说,就所有可能的方向而言,如果所有数据投影到该向量定义的直线上,则结果值将具有最大方差。与次大特征值相关联的特征向量(正交于第一个特征向量)是具有最大剩余方差的数据的方向。
协方差矩阵S的特征向量定义了一个新的坐标系。PCA可以看作原坐标系到新坐标系的旋转变换。新坐标轴按数据的变异性排列。变换保持数据的总变异性,但是新属性是不相关的。
二、MADlib的PCA相关函数
1. 训练函数
MADlib中PCA的实现是使用一种分布式的SVD(奇异值分解)找出主成分,而不是直接计算方差矩阵的特征向量。PCA和SVD是两种密切相关的技术,它们假定新旧变量集合之间存在线性关系。
设X为与原始数据矩阵,![]() 为X的列平均值向量。PCA首先将原始矩阵标准化为矩阵
为X的列平均值向量。PCA首先将原始矩阵标准化为矩阵![]() :
:
![]()
其中![]() 是所有的行向量。然后MADlibPCA函数对矩阵
是所有的行向量。然后MADlibPCA函数对矩阵![]() 进行SVD分解:
进行SVD分解:
其中∑是对角矩阵,特征值为![]() 的条目,主成分是V的行。最后使用贝塞尔修正(Bessel's correction)用N-1代替N计算协方差。
的条目,主成分是V的行。最后使用贝塞尔修正(Bessel's correction)用N-1代替N计算协方差。
这种实现的重要前提是假设用户只使用具有非零特征值的主成分,因为SVD计算用的是Lanczos算法,它并不保证含有零特征值的奇异向量的正确性。
(1) 语法
稠密矩阵和稀疏矩阵的训练函数有所不同。稠密矩阵训练函数为:
pca_train (source_table,
out_table,
row_id,
components_param,
grouping_cols,
lanczos_iter,
use_correlation,
result_summary_table)稀疏矩阵训练函数为:
pca_sparse_train (source_table,
out_table,
row_id,
col_id, -- 只针对稀疏矩阵
val_id, -- 只针对稀疏矩阵
row_dim, -- 只针对稀疏矩阵
col_dim, -- 只针对稀疏矩阵
components_param,
grouping_cols,
lanczos_iter,
use_correlation,
result_summary_table )(2) 参数
参数名称 |
数据类型 |
描述 |
source_table |
TEXT |
PCA训练数据的输入表名。输入的数据矩阵应该具有N行M列,N为记录数,M为每条记录的特征数。 |
out_table |
TEXT |
输出表的名称。有两种可能的输出表:主输出表和均值输出表。 |
row_id |
TEXT |
输入表中表示行ID的列名。该列应该为整型,值域为1到N,对于稠密矩阵格式,该列应该包含从1到N的连续整数。 |
col_id |
TEXT |
稀疏矩阵中表示列ID的列名。列应为整型,值域为1到M。该参数只用于稀疏矩阵。 |
val_id |
TEXT |
稀疏矩阵中表示非零元素值的列名。该参数只用于稀疏矩阵。 |
row_dim |
INTEGER |
矩阵的实际行数,指的是当矩阵转换为稠密矩阵时所具有的行数。该参数只用于稀疏矩阵。 |
col_dim |
INTEGER |
矩阵的实际列数,指的是当矩阵转换为稠密矩阵时所具有的列数。该参数只用于稀疏矩阵。row_dim和col_dim实际上可以从稀疏矩阵推断出,当前是为了向后兼容而存在,将来会被移除。这两个值大于矩阵的实际值时会补零。 |
components_param |
INTEGER或FLOAT |
该参数控制如何从输入数据确定主成分的数量。如果为INTEGER类型,代表需要计算的主成分的个数。如果为FLOAT类型,算法将返回足够的主成分向量,使得累积特征值大于此参数(标准差比例)。 |
grouping_cols(可选) |
TEXT |
缺省值为NULL。指定逗号分隔的列名,使用此参数的所有列分组,对每个分组独立计算PCA。稠密矩阵的各分组大小可能不同,而稀疏矩阵的每个分组大小都一样,因为稀疏矩阵的‘row_dim’和‘col_dim’是跨所有组的全局参数。 |
lanczos_iter(可选) |
INTEGER |
缺省值为k+40与最小矩阵维度的较小者,k是主成分数量。此参数定义计算SVD时的Lanczos迭代次数,迭代次数越大精度越高,同时计算越花时间。迭代次数不能小于k值,也不能大于最小矩阵维度。如果此参数设置为0,则使用缺省值。如果‘lanczos_iter’和‘components_param’参数同时设置,在确定主成分数量时,优先考虑‘lanczos_iter’。 |
use_correlation(可选) |
BOOLEAN |
缺省值为FALSE。指定在计算主成分时,是否使用相关矩阵代替协方差矩阵。当前该参数仅用于向后兼容,因此必须设置为false。 |
result_summary_table(可选) |
TEXT |
缺省值为NULL。指定概要表的名称,NULL时不生成概要表。 |
表1 pca_train和pca_sparse_train函数参数说明
PCA的稠密输入表可以使用两种标准的MADlib稠密矩阵格式:
{TABLE|VIEW} source_table (
row_id INTEGER,
row_vec FLOAT8[],
…)或者:
{TABLE|VIEW} source_table (
row_id INTEGER,
col1 FLOAT8,
col2 FLOAT8,
…)注意row_id作为入参是输入矩阵的行标识,必须是从1开始且连续的整数。
PCA的稀疏矩阵输入表的格式如下,其中row_id和col_id列指示矩阵下标,是正整数,val_id列定义非0的矩阵元素值。
{TABLE|VIEW} source_table (
…
row_id INTEGER,
col_id INTEGER,
val_id FLOAT8,
…)主输出表(out_table)包含特征值最高的k个主成分的特征向量,k值直接由用户参数指定,或者根据方差的比例计算得出。主输出表包含以下四列:
- row_id:特征值倒序排名。
- principal_components:包含主成分元素的向量(特征向量)。
- std_dev:每个主成分的标准差。
- proportion:每个主成分标准差所占的比例。
均值输出表(out_table_mean)包含列的均值,只有一列:
- column_mean:包含输入矩阵的列的均值。
‘components_param’的值域为正整数或(0.0,1.0]。这里要注意整型和浮点数的区别,如果components_param指定为1,则返回一个主成分,而指定为1.0时,返回所有的主成分,因为此时方差比例为100%。还要注意一点,主成分数量是全局的。在分组时(由grouping_cols参数指定)可能选择标准差比例更好,因为这可以使不同分组具有不同的主成分数量。
概要表(result_summary_table)具有下面的列:
- rows_used:INTEGER类型,输入数据的行数。
- exec_time (ms):FLOAT8类型,函数执行的毫秒数。
- iter:INTEGER类型,SVD计算时的迭代次数。
- recon_error:FLOAT8类型,SVD近似值的绝对误差。
- relative_recon_error:FLOAT8类型,SVD近似值的相对误差。
- use_correlation:BOOLEAN类型,为真表示使用的是相关矩阵。
(3) 联机帮助
可以执行下面的查询获得PCA训练函数的联机帮助。
select madlib.pca_train('usage');
select madlib.pca_sparse_train('usage');2. 投影函数
给定包含主成分P的输入数据矩阵X,对应的降维后的低维度矩阵为X',其计算公式为:
其中![]() 是的列平均值,
是的列平均值,![]() 是所有的行向量。这步计算的结果近似于原始数据,保留了绝大部分的原始信息。
是所有的行向量。这步计算的结果近似于原始数据,保留了绝大部分的原始信息。
残余表用于估计降维后的矩阵与原始输入数据的近似程度,其计算公式为:
![]()
如果残余矩阵的元素接近于零,则表示降维后的信息丢失很少,基本相当于原始数据。残差范数表示为:
![]()
其中![]() 是Frobenius范数。相对残差范数的计算公式为:
是Frobenius范数。相对残差范数的计算公式为:
(1) 语法
稠密矩阵和稀疏矩阵的投影函数有所不同。稠密矩阵投影函数为:
pca_project (source_table,
pc_table,
out_table,
row_id,
residual_table,
result_summary_table)稀疏矩阵的投影函数为:
pca_sparse_project (source_table,
pc_table,
out_table,
row_id,
col_id, -- 只针对稀疏矩阵
val_id, -- 只针对稀疏矩阵
row_dim, -- 只针对稀疏矩阵
col_dim, -- 只针对稀疏矩阵
residual_table,
result_summary_table)
(2) 参数
参数名称 |
数据类型 |
描述 |
source_table |
TEXT |
等同于PCA训练函数,指定源表名称。输入数据矩阵应该有N行M列,N为数据点个数,M为每个数据点的特征数。与PCA训练函数类似,pca_project函数的输入表格式,应该为MADlib两种标准稠密矩阵格式之一,而pca_sparse_project函数的输入表应该为MADlib的标准稀疏矩阵格式。 |
pc_table |
TEXT |
主成分表名,通常使用PCA训练函数的主输出表。 |
out_table |
TEXT |
输入数据降维后的输出表名称。 |
row_id |
TEXT |
同PCA训练函数。 |
col_id |
TEXT |
同PCA训练函数。 |
val_id |
TEXT |
同PCA训练函数。 |
row_dim |
INTEGER |
同PCA训练函数。 |
col_dim |
INTEGER |
同PCA训练函数。 |
residual_table(可选) |
TEXT |
缺省值为NULL,残余表的名称。 |
result_summary_table(可选) |
TEXT |
缺省值为NULL,结果概要表的名称。 |
表2 pca_project和pca_sparse_project函数参数说明
out_table是一个投影到主成分上的稠密矩阵,具有以下两列:
- row_id:输出矩阵的行ID。
- row_vec:矩阵行中所含的向量。
residual_table表现为一个稠密矩阵,具有以下两列:
- row_id:输出矩阵的行ID。
- row_vec:包含残余矩阵行元素的向量。
result_summary_table中含有PCA投影函数的性能信息,具有以下三列:
- exec_time:函数执行所用的时间(毫秒)。
- residual_norm:绝对误差。
- relative_residual_norm:相对误差。
(3) 联机帮助
可以执行下面的查询获得PCA投影函数的联机帮助。
select madlib.pca_project('usage');
select madlib.pca_sparse_project('usage');三、PCA应用示例
我们用一个企业综合实力排序的例子说明MADlib PCA的用法。为了系统地分析某IT类企业的经济效益,选择了8个不同的利润指标,对15家企业进行了调研,并得到如表3所示的数据。现在需要根据根据这些数据对15家企业进行综合实例排序。
企业编号 |
净利润率(%) |
固定资产利润率(%) |
总产值利润率(%) |
销售收入利润率(%) |
产品成本利润率(%) |
物耗利润率(%) |
人均利润(千元/人) |
流动资产利润率(%) |
1 |
40.4 |
24.7 |
7.2 |
6.1 |
8.3 |
8.7 |
2.442 |
20 |
2 |
25 |
12.7 |
11.2 |
11 |
12.9 |
20.2 |
3.542 |
9.1 |
3 |
13.2 |
3.3 |
3.9 |
4.3 |
4.4 |
5.5 |
0.578 |
3.6 |
4 |
22.3 |
6.7 |
5.6 |
3.7 |
6 |
7.4 |
0.176 |
7.3 |
5 |
34.3 |
11.8 |
7.1 |
7.1 |
8 |
8.9 |
1.726 |
27.5 |
6 |
35.6 |
12.5 |
16.4 |
16.7 |
22.8 |
29.3 |
3.017 |
26.6 |
7 |
22 |
7.8 |
9.9 |
10.2 |
12.6 |
17.6 |
0.847 |
10.6 |
8 |
48.4 |
13.4 |
10.9 |
9.9 |
10.9 |
13.9 |
1.772 |
17.8 |
9 |
40.6 |
19.1 |
19.8 |
19 |
29.7 |
39.6 |
2.449 |
35.8 |
10 |
24.8 |
8 |
9.8 |
8.9 |
11.9 |
16.2 |
0.789 |
13.7 |
11 |
12.5 |
9.7 |
4.2 |
4.2 |
4.6 |
6.5 |
0.874 |
3.9 |
12 |
1.8 |
0.6 |
0.7 |
0.7 |
0.8 |
1.1 |
0.056 |
1 |
13 |
32.3 |
13.9 |
9.4 |
8.3 |
9.8 |
13.3 |
2.126 |
17.1 |
14 |
38.5 |
9.1 |
11.3 |
9.5 |
12.2 |
16.4 |
1.327 |
11.6 |
15 |
26.2 |
10.1 |
5.6 |
15.6 |
7.7 |
30.1 |
0.126 |
25.9 |
表3 企业综合实例评价表
由于本问题中涉及8个指标,这些指标间的关联关系并不明确,而且各指标数值的数量级也有差异,为此这里将首先借助PCA方法对指标体系进行降维处理,然后根据PCA打分结果实现对企业的综合实力排序。
1. 创建原始稠密矩阵表并添加数据
drop table if exists mat;
create table mat (id integer, row_vec double precision[]);
insert into mat values
(1, '{40.4, 24.7, 7.2, 6.1, 8.3, 8.7, 2.442, 20}'),
(2, '{ 25, 12.7, 11.2, 11, 12.9, 20.2, 3.542, 9.1}'),
(3, '{13.2, 3.3, 3.9, 4.3, 4.4, 5.5, 0.578, 3.6}'),
(4, '{22.3, 6.7, 5.6, 3.7, 6, 7.4, 0.176, 7.3}'),
(5, '{34.3, 11.8, 7.1, 7.1, 8, 8.9, 1.726, 27.5}'),
(6, '{35.6, 12.5, 16.4, 16.7, 22.8, 29.3, 3.017, 26.6}'),
(7, '{ 22, 7.8, 9.9, 10.2, 12.6, 17.6, 0.847, 10.6}'),
(8, '{48.4, 13.4, 10.9, 9.9, 10.9, 13.9, 1.772, 17.8}'),
(9, '{40.6, 19.1, 19.8, 19, 29.7, 39.6, 2.449, 35.8}'),
(10, '{24.8, 8, 9.8, 8.9, 11.9, 16.2, 0.789, 13.7}'),
(11, '{12.5, 9.7, 4.2, 4.2, 4.6, 6.5, 0.874, 3.9}'),
(12, '{ 1.8, 0.6, 0.7, 0.7, 0.8, 1.1, 0.056, 1}'),
(13, '{32.3, 13.9, 9.4, 8.3, 9.8, 13.3, 2.126, 17.1}'),
(14, '{38.5, 9.1, 11.3, 9.5, 12.2, 16.4, 1.327, 11.6}'),
(15, '{26.2, 10.1, 5.6, 15.6, 7.7, 30.1, 0.126, 25.9}'); 2. 调用PCA训练函数生成特征向量矩阵
drop table if exists result_table, result_table_mean;
select madlib.pca_train('mat', -- 原始表
'result_table', -- 输出表
'id', -- 源表ID列
4 -- 主成分个数
); 3. 查看输出表
select row_id id, std, prop,
lpad(p1,6,' ')||','||lpad(p2,6,' ')||','||
lpad(p3,6,' ')||','||lpad(p4,6,' ')||','||
lpad(p5,6,' ')||','||lpad(p6,6,' ')||','||
lpad(p7,6,' ')||','||lpad(p8,6,' ') principal_components
from (select row_id,
round(p[1]::numeric,3) p1,
round(p[2]::numeric,3) p2,
round(p[3]::numeric,3) p3,
round(p[4]::numeric,3) p4,
round(p[5]::numeric,3) p5,
round(p[6]::numeric,3) p6,
round(p[7]::numeric,3) p7,
round(p[8]::numeric,3) p8,
round(std_dev::numeric,3) std,
round(proportion::numeric,3) prop
from (select row_id, principal_components p, std_dev, proportion
from result_table) t) t
order by row_id;结果:
id | std | prop | principal_components
----+--------+-------+---------------------------------------------------------
1 | 19.487 | 0.744 | -0.550,-0.221,-0.222,-0.234,-0.324,-0.460,-0.035,-0.477
2 | 9.067 | 0.161 | -0.679,-0.258, 0.092, 0.224, 0.255, 0.590,-0.019, 0.009
3 | 5.063 | 0.050 | 0.293,-0.117, 0.358, 0.036, 0.371, 0.070, 0.056,-0.791
(3 rows) 可以看到,主成分数量为3时,累积标准差比例为95.5,即反映了95.5%的原始信息,而维度已经从8个降低为3个。可以用下面的查询求得降维前后的方差验证PCA训练的结果。
查询原始数据方差:
select sum(power(row_vec[1] - avg1,2))/14+
sum(power(row_vec[2] - avg2,2))/14+
sum(power(row_vec[3] - avg3,2))/14+
sum(power(row_vec[4] - avg4,2))/14+
sum(power(row_vec[5] - avg5,2))/14+
sum(power(row_vec[6] - avg6,2))/14+
sum(power(row_vec[7] - avg7,2))/14+
sum(power(row_vec[8] - avg8,2))/14 variance_org
from mat t1,
(select avg(row_vec[1]) avg1,
avg(row_vec[2]) avg2,
avg(row_vec[3]) avg3,
avg(row_vec[4]) avg4,
avg(row_vec[5]) avg5,
avg(row_vec[6]) avg6,
avg(row_vec[7]) avg7,
avg(row_vec[8]) avg8
from mat) t2;结果:
variance_org
--------------
510.3914286
(1 row)查询PCA降维后的方差:
select sum(power(row_vec[1] - avg1,2))/14+
sum(power(row_vec[2] - avg2,2))/14+
sum(power(row_vec[3] - avg3,2))/14 variance_pca
from out_table t1,
(select avg(row_vec[1]) avg1,
avg(row_vec[2]) avg2,
avg(row_vec[3]) avg3
from out_table) t2;结果:
variance_pca
------------------
487.555008124347
(1 row)4. 调用PCA投影函数生成降维后的数据表
drop table if exists residual_table, result_summary_table, out_table;
select madlib.pca_project( 'mat',
'result_table',
'out_table',
'id',
'residual_table',
'result_summary_table');5. 查看投影函数输出表
查询投影后的数据表:
select * from out_table order byrow_id; 结果:
row_id | row_vec
--------+----------------------------------------------------------
1 | {7.08021173666004,-17.6113408380368,3.62504928877282}
2 | {-0.377499074086429,5.25083911315586,-6.06667264391957}
3 | {-24.3659516926199,2.69294552046529,-0.854680487274518}
4 | {-15.235298685282,-2.7756923532236,-1.48789032627869}
5 | {4.64264829479035,-9.80192214158058,9.97441166441563}
6 | {23.6146598612176,7.91277187194796,-1.70125446716029}
7 | {-4.25445515316499,6.71053107113929,-3.63489574437095}
8 | {12.8547303317577,-15.2151276724561,-4.53202062778529}
9 | {40.4531114732088,11.566606363421,0.33351408976578}
10 | {-2.39187210257759,3.48063922820141,-1.53633678788746}
11 | {-22.6173674430242,2.15970955881415,0.0711392924992467}
12 | {-37.2273102800874,6.50778045364591,3.06216108712084}
13 | {2.45676837959725,-5.55018275237518,0.715863146049782}
14 | {5.05828673790116,-5.6726215744102,-7.79762716115411}
15 | {10.3093376158273,10.3450641508798,9.82923967771456}
(15 rows) 查询概要表:
select * from result_summary_table;结果:
exec_time | residual_norm | relative_residual_norm
---------------+---------------+------------------------
7834.64002609 | 17.8804330669 | 0.0999460602087
(1 row) 查询残余表:
select row_id,
lpad(round(row_vec[1]::numeric,3),6,' ')||', '||
lpad(round(row_vec[2]::numeric,3),6,' ')||', '||
lpad(round(row_vec[3]::numeric,3),6,' ')||', '||
lpad(round(row_vec[4]::numeric,3),6,' ')||', '||
lpad(round(row_vec[5]::numeric,3),6,' ')||', '||
lpad(round(row_vec[6]::numeric,3),6,' ')||', '||
lpad(round(row_vec[7]::numeric,3),6,' ')||', '||
lpad(round(row_vec[8]::numeric,3),6,' ') row_vec
from residual_table order by row_id; 结果:
row_id | row_vec
--------+----------------------------------------------------------------
1 | -2.253, 7.276, -0.316, -0.494, 1.005, 0.433, 0.599, -1.523
2 | -0.863, 3.954, -0.237, 0.678, -1.408, 1.207, 1.860, -1.401
3 | 0.308, -1.423, -0.116, 0.357, 0.447, -0.586, -0.021, 0.445
4 | 0.490, -1.375, -0.164, -1.179, 0.250, 0.294, -0.884, 0.337
5 | 0.153, -3.813, 1.675, -0.442, 1.857, -2.405, 0.477, 2.049
6 | -0.359, -1.362, 0.957, 0.324, 1.662, -1.994, 0.792, 1.175
7 | -0.028, 0.002, 0.058, 0.547, 0.078, -0.300, -0.534, 0.012
8 | 1.811, -3.726, -1.035, 1.121, -1.902, 0.993, -0.685, -0.048
9 | -1.533, 2.229, 1.013, -2.063, 2.932, -1.451, -0.181, 0.700
10 | 0.169, -1.288, 0.593, -0.389, 0.377, -0.506, -0.602, 0.592
11 | -1.443, 4.345, 0.176, 0.001, 0.560, -0.011, 0.256, -0.817
12 | -0.284, -0.759, 0.585, -0.944, 1.492, -1.045, 0.202, 0.850
13 | -0.471, 0.949, 0.756, -0.019, -0.154, -0.154, 0.516, -0.023
14 | 1.721, -3.462, -0.954, 0.290, -1.723, 1.225, -0.855, -0.029
15 | 2.584, -1.547, -2.992, 2.213, -5.472, 4.300, -0.938, -2.318
(15 rows) out_table为降维后,投影到主成分的数据表。residual_table中的数据表示与每个原始数据项对应的误差,越接近零说明误差越小。result_summary_table表中包含函数执行概要信息。
6. 按主成分总得分降序排列得到综合实力排序
select row_id id, row_vec, round(madlib.array_sum(row_vec)::numeric,4) r
from out_table
order by r desc;结果:
id | row_vec | r
----+----------------------------------------------------------+-----------
9 | {40.4531114732088,11.566606363421,-0.333514089765778} | 51.6862
6 | {23.6146598612176,7.91277187194796,1.70125446716029} | 33.22869
2 | {-0.377499074086431,5.25083911315585,6.06667264391957} | 10.9400
15 | {10.3093376158273,10.3450641508798,-9.82923967771456} | 10.8252
14 | {5.05828673790117,-5.6726215744102,7.79762716115411} | 7.1833
7 | {-4.254455153165,6.71053107113929,3.63489574437095} | 6.0910
10 | {-2.3918721025776,3.48063922820141,1.53633678788746} | 2.6251
8 | {12.8547303317577,-15.2151276724561,4.53202062778528} | 2.1716
13 | {2.45676837959725,-5.55018275237518,-0.715863146049783} | -3.8093
1 | {7.08021173666005,-17.6113408380368,-3.62504928877282} | -14.1562
5 | {4.64264829479035,-9.80192214158058,-9.97441166441563} | -15.1337
4 | {-15.235298685282,-2.7756923532236,1.48789032627869} | -16.5231
11 | {-22.6173674430242,2.15970955881415,-0.0711392924992431} | -20.5288
3 | {-24.3659516926199,2.69294552046528,0.85468048727452} | -20.8183
12 | {-37.2273102800874,6.50778045364591,-3.06216108712083} | -33.7817
(15 rows) 从该结果可知,第9家企业的综合实力最强,第12家企业的综合实力最弱。row_vec中的三列为个主成分的得分。以上应用示例比较简单,真实场景中,PCA方法还要根据实际问题和需求灵活使用。