控制教程 —— 介绍篇:4.根轨迹控制器设计
在本教程中,我们将介绍根轨迹,展示如何使用MATLAB来创建根轨迹,并演示如何通过使用根轨迹来设计满足某些性能指标的反馈控制器。
本教程中使用的主要MATLAB命令包括:
文章目录
-
- 闭环极点
- 绘制传递函数的根轨迹
- 从根轨迹选择K的值
- 闭环响应
- 使用控制系统设计器进行根轨迹设计
闭环极点
开环传递函数 H ( s ) H(s) H(s) 的根轨迹通常是在比例增益 K K K 在0到 ∞ \infty ∞ 变化时,形成的闭环极点的轨迹曲线。下图显示了单位反馈架构,对于任何开环传递函数 H ( s ) H(s) H(s) ,即使开环传递函数的某些元素在反馈路径中,根轨迹的过程也都是相同的。
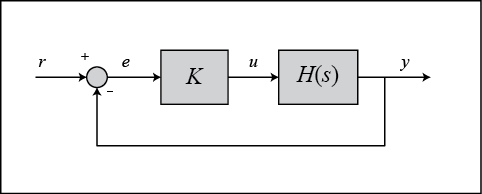
在这种情况下,闭环传递函数为:
Y ( s ) R ( s ) = K H ( s ) 1 + K H ( s ) \frac{Y(s)}{R(s)} = \frac{KH(s)}{1 + KH(s)} R(s)Y(s)=1+KH(s)KH(s)
因此,闭环系统的极点是 s s s 的值,使得 1 + K H ( s ) = 0 1+KH(s)=0 1+KH(s)=0
如果我们写 H ( s ) = b ( s ) / a ( s ) H(s)=b(s)/a(s) H(s)=b(s)/a(s) ,则该等式可以重写为:
⇒ a ( s ) + K b ( s ) = 0 \Rightarrow\ a(s) + Kb(s) = 0 ⇒ a(s)+Kb(s)=0 ⇒ a ( s ) K + b ( s ) = 0 \Rightarrow\ \frac{a(s)}{K} + b(s) = 0 ⇒ Ka(s)+b(s)=0
假设 n n n 是 a ( s ) a(s) a(s) 的阶数, m m m 是 b ( s ) b(s) b(s) 的阶数(多项式的阶数对应于 s s s 的最高次幂)。
我们将考虑 K K K 的所有正值。在 K → 0 K\rightarrow 0 K→0的极限中,闭环系统的极点是 a ( s ) = 0 a(s)=0 a(s)=0 的解( H ( s ) H(s) H(s) 的极点)。在 K → ∞ K\rightarrow \infty K→∞ 的极限中,闭环系统的极点是 b ( s ) = 0 b(s) = 0 b(s)=0 ( H ( s ) H(s) H(s)的零点)的解。
无论我们选择 K K K,闭环系统都有 n n n 个极点,其中 n n n 是开环传递函数 H ( s ) H(s) H(s) 的极点数。然后,根轨迹具有 n n n个分支,每个分支都从 H ( s ) H(s) H(s) 的极点开始,并接近 H ( s ) H(s) H(s) 的零点。如果 H ( s ) H(s) H(s) 的极点多于零点(通常都是这样),即 m < n m
由于根轨迹由所有可能的闭环极点的位置组成,因此根轨迹可帮助我们选择增益 K K K 的值,以实现所需的性能类型。如果任何选定的极点在右半复平面上,则闭环系统将不稳定。最接近虚轴的极点对闭环响应的影响最大,因此,即使系统具有三个或四个极点,它的表现仍可能类似于二阶或一阶系统,具体取决于主导极点的位置。
绘制传递函数的根轨迹
考虑一个具有以下传递函数的开环系统:
H ( s ) = Y ( s ) U ( s ) = s + 7 s ( s + 5 ) ( s + 15 ) ( s + 20 ) H(s) = \frac{Y(s)}{U(s)} = \frac{s + 7}{s(s + 5)(s + 15)(s + 20)} H(s)=U(s)Y(s)=s(s+5)(s+15)(s+20)s+7我们如果使用根轨迹为系统设计反馈控制器,假设我们的设计标准是5%的过冲和1s的上升时间,可以使用如下命令:
s = tf('s');
sys = (s + 7)/(s*(s + 5)*(s + 15)*(s + 20));
rlocus(sys)
axis([-22 3 -15 15])
从根轨迹选择K的值
上图显示了纯比例控制器的所有可能的闭环极点位置,在这种情况下,并非所有这些闭环极点位置都满足我们的设计标准。为了确定轨迹的哪一部分可以接受,我们可以使用sgrid(zeta,wn)命令绘制恒定阻尼比和自然频率的线。它的两个参数是阻尼比( ζ \zeta ζ)和自然频率( ω n \omega_n ωn)[如果是想查看可接受的范围,则它们是一个向量]。在我们的问题中,我们需要一个小于5%的超调(这意味着阻尼比 ζ \zeta ζ 大于0.7)①和一个上升时间为1s(这意味着自然频率 ω n \omega_n ωn 大于1.8)②。在MATLAB命令窗口中输入以下内容:
①: 0.05 > M p = e ( − ζ π 1 − ζ 2 ) 0.05 >Mp= e^{\left( \frac{-\zeta\pi}{\sqrt{1-\zeta^2}} \right)} 0.05>Mp=e(1−ζ2−ζπ) ⇒ ζ > 0.6906 \Rightarrow \zeta>0.6906 ⇒ζ>0.6906
②: 1 > T r ≈ 1.8 ω n 1>T_r \approx \frac{1.8}{\omega_n} 1>Tr≈ωn1.8 ⇒ ω n > 1.8 \Rightarrow \omega_n>1.8 ⇒ωn>1.8
zeta = 0.7;
wn = 1.8;
sgrid(zeta,wn)

在上面的图中,两条呈45°角的虚线表示极点位置,其中 ζ = 0.7 \zeta =0.7 ζ=0.7;
在这些线之间 ζ > 0.7 \zeta>0.7 ζ>0.7,而在这些线之外 ζ < 0.7 \zeta<0.7 ζ<0.7。半圆表示自然频率 ω m = 1.8 \omega_m = 1.8 ωm=1.8 的极点位置,在圆内 ω n < 1.8 \omega_n<1.8 ωn<1.8,在圆外 o m e g a n > 1.8 omega_n>1.8 omegan>1.8。
回到我们的问题,要使超调量小于5%,极点必须位于两条带角度的虚线之间,并且要使上升时间短于1s,极点必须位于虚线半圆之外。因此,现在我们知道根轨迹的哪一部分(可能的闭环极点位置)可以满足我们的要求。另外该位置的所有极点都在左半平面中,因此闭环系统是稳定的。
从上图可以看出,所需区域内有一部分根轨迹,因此,在这种情况下,我们只需要一个比例控制器即可将极点移至所需区域。您可以在MATLAB中使用rlofind命令在轨迹上选择所需要的极点:
[k,poles] = rlocfind(sys)
在图上单击您想要闭环极点的点,您可能希望选择下图中指示的点,以满足设计需求。

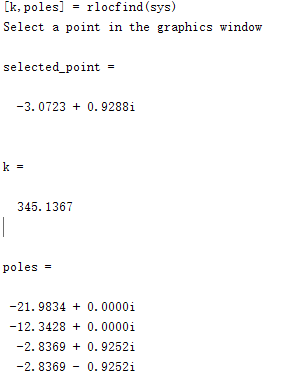
请注意,由于根轨迹可能具有多个分支,因此当您选择一个极点时,您还要确定其他闭环极点在何处,所有这些极点对应的相同的 K K K。请记住,这些极点也会影响响应,从上图可以看出,在选择的四个极点(由 “+”号表示)中,最接近虚轴的两个极点位于我们所需的区域中。由于这些极点趋于主极点,因此我们可以确信,对于具有 K K K 的比例控制器,可以满足期望要求。
闭环响应
为了验证阶跃响应,您需要了解闭环传递函数。您可以使用框图简化规则来进行计算,或者让MATLAB为您完成(如果使用rlocfind,则无需输入K的值)。
K = 350;
sys_cl = feedback(K*sys,1)

函数feedback的两个参数是开环传递函数的前馈路径中的传递函数和反馈路径中的传递函数。在这种情况下,我们的系统是单位反馈。
如果遇到非单位反馈的情况,请查看MATLAB函数feedback的帮助文件,该文件演示了如何获取具有增益的反馈路径中的传递函数。
用选择的 K K K 来查看闭环系统的阶跃响应:
step(sys_cl)

正如我们预期的那样,该响应的过冲小于5%,上升时间小于1s。
使用控制系统设计器进行根轨迹设计
完成上述操作的另一个方法是使用MATLAB中的交互式"控制系统设计器"工具,针对上述相同的模型,我们首先定义传递函数 H ( s ) H(s) H(s):
s = tf('s');
plant = (s + 7)/(s*(s + 5)*(s + 15)*(s + 20));
controlSystemDesigner函数可用于分析和设计,在这种情况下。我们将专注于根轨迹作为设计方法来改善闭环系统的阶跃响应。首先,在MATLAB命令窗口中输入以下内容:
controlSystemDesigner(plant)
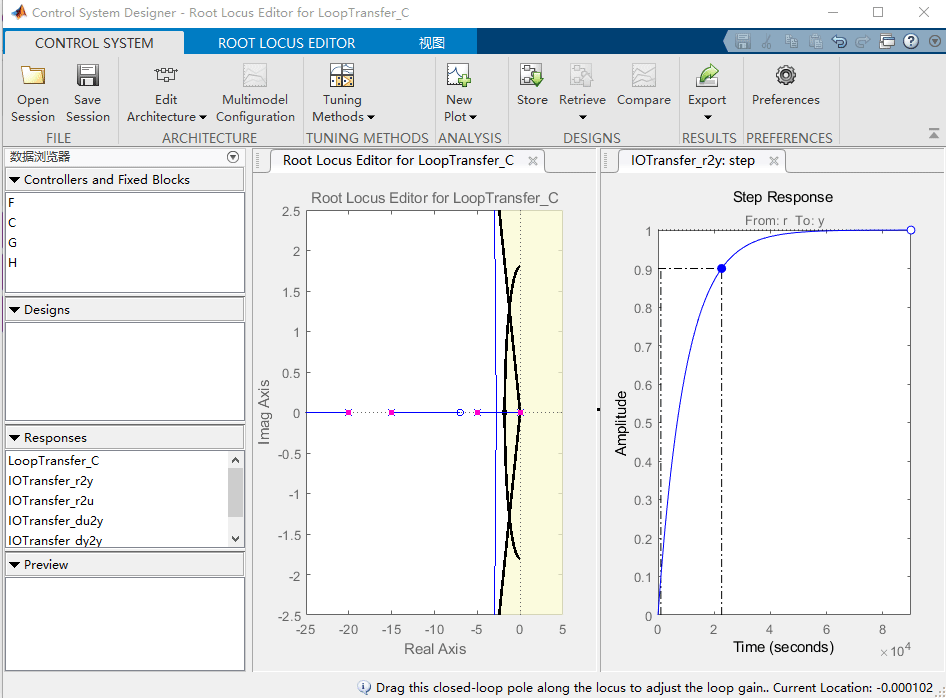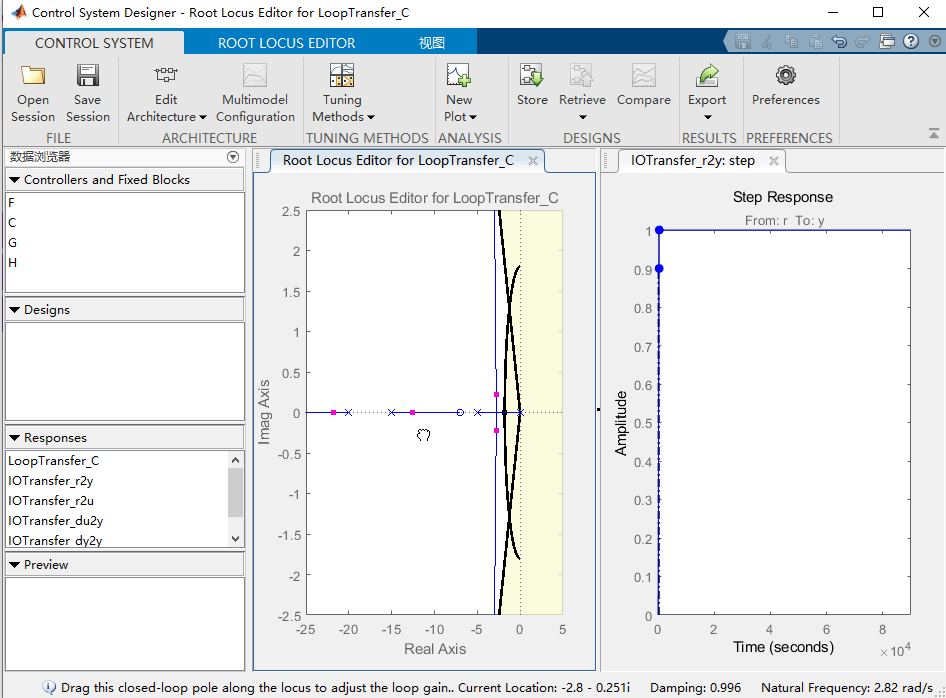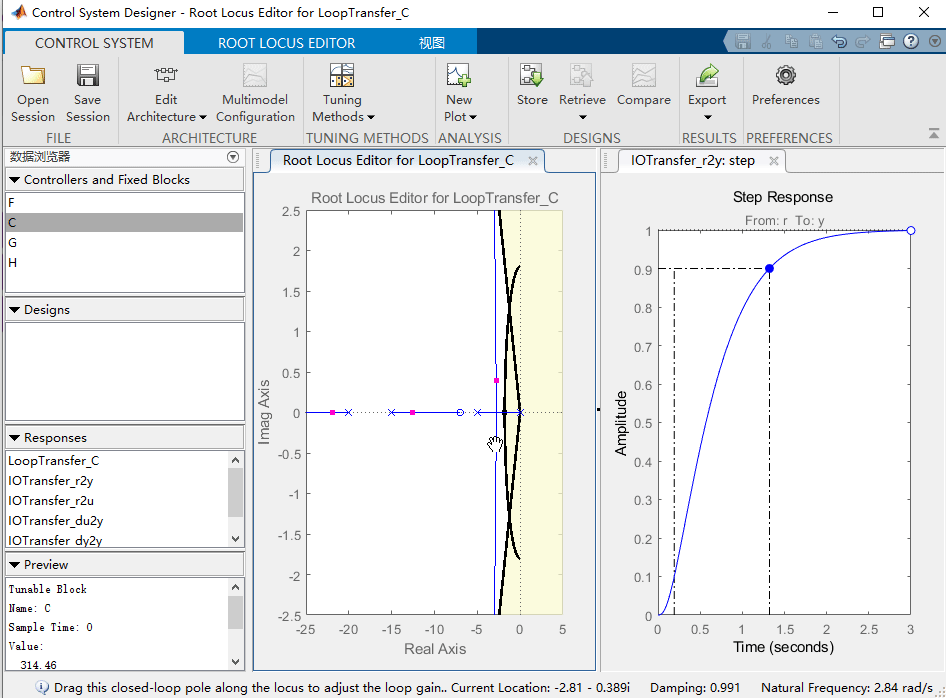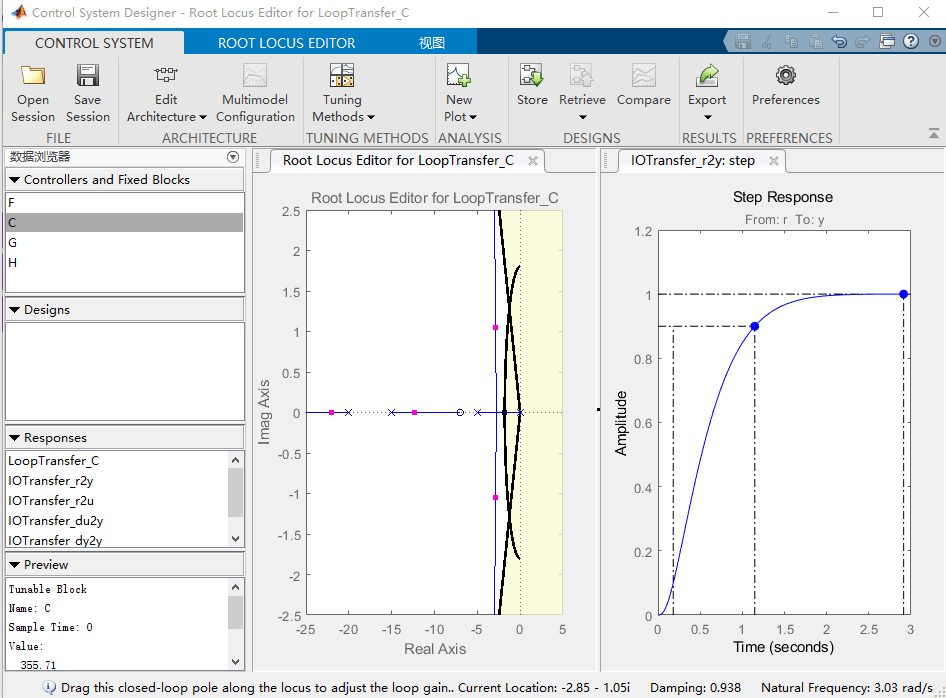
应出现以下窗口。您也可以通过转到“APP“选项卡并单击控制系统与优化的应用程序来启用GUI,在这里,您可以看到根轨迹以及开环Bode图和给定系统在单位反馈中使用默认控制器 K = 1 K=1 K=1 的闭环阶跃响应。
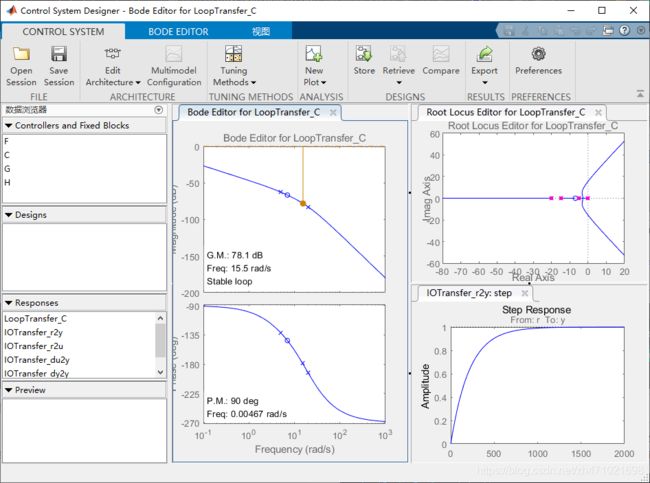
下一步是将设计要求添加到”根轨迹“图中,右键设计需求,然后单击新建,直接在图上完成。可以为稳定时间,超调百分比,阻尼比,自然频率,区域约束,设置系统要求。
在这里,我们将设置阻尼比和自然频率的设计要求,就像之前使用sgrid命令所做的那样,回想一下,我们需求的边界要求 ζ = 0.7 \zeta=0.7 ζ=0.7, ω n = 1.8 \omega_n=1.8 ωn=1.8。在设计要求内进行设置。在图中,任何仍为白色的区域都是闭环极点可以接受的区域。

右键单击某个轴并选择属性,然后选择极限,以放大根轨迹,将实轴限制更改为-25到5,将虚轴限制更改为-2.5到2.5。

同样,我们可以查看相应的关键参数,在阶跃响应图上,右键单击该图,然后转到特性并选择峰值响应和上升时间。屏幕上现在应该有两个大圆点,指示这些参数的值。单击这些点中的每一个,将弹出一个包含信息的框。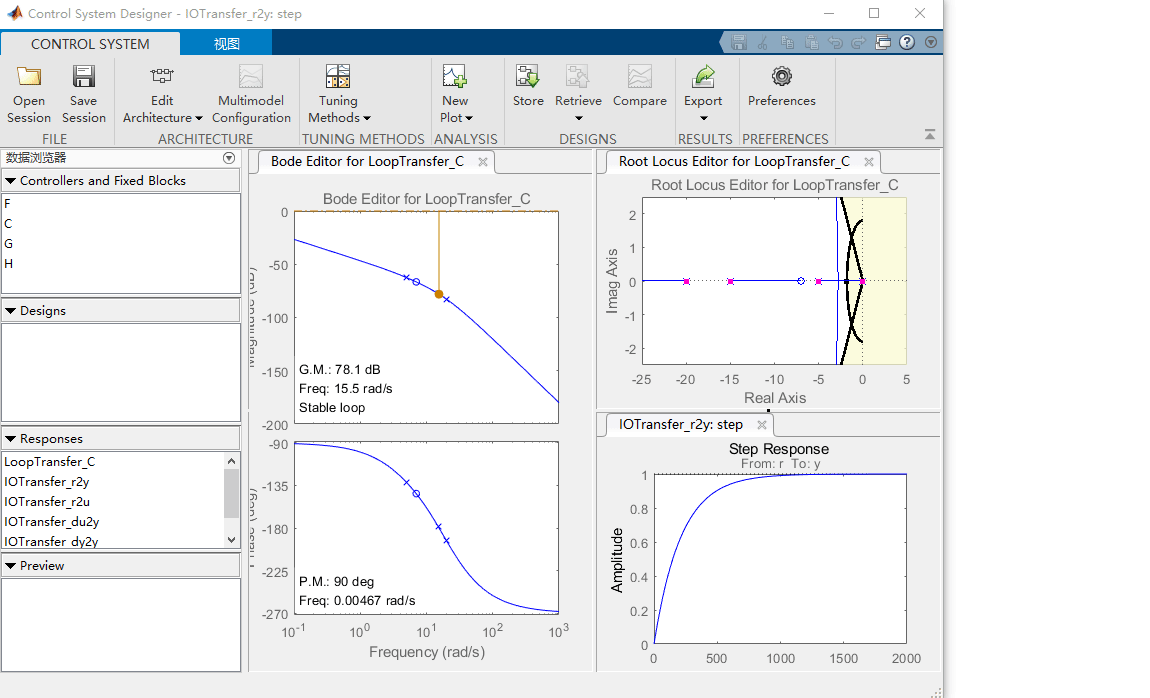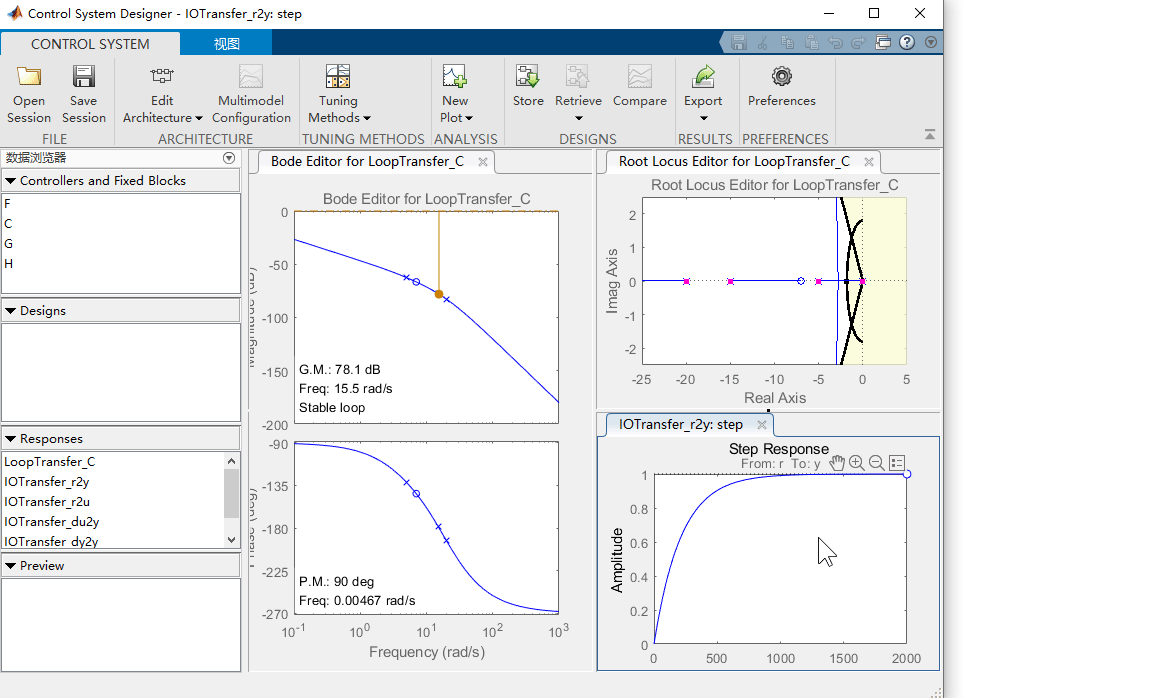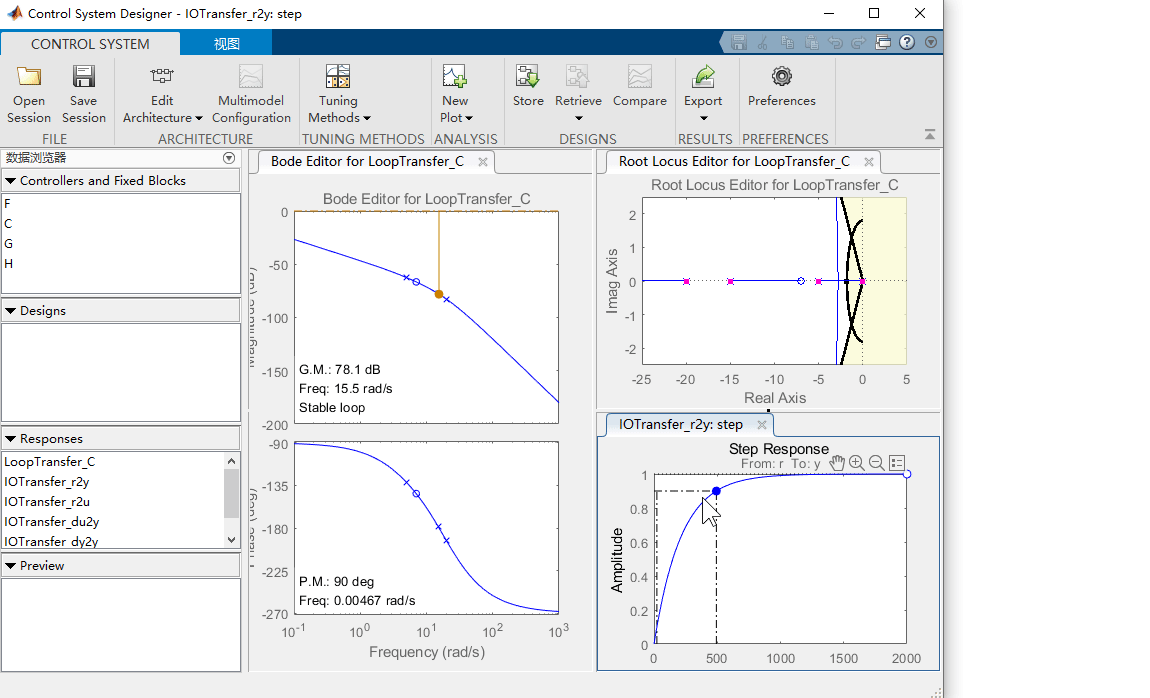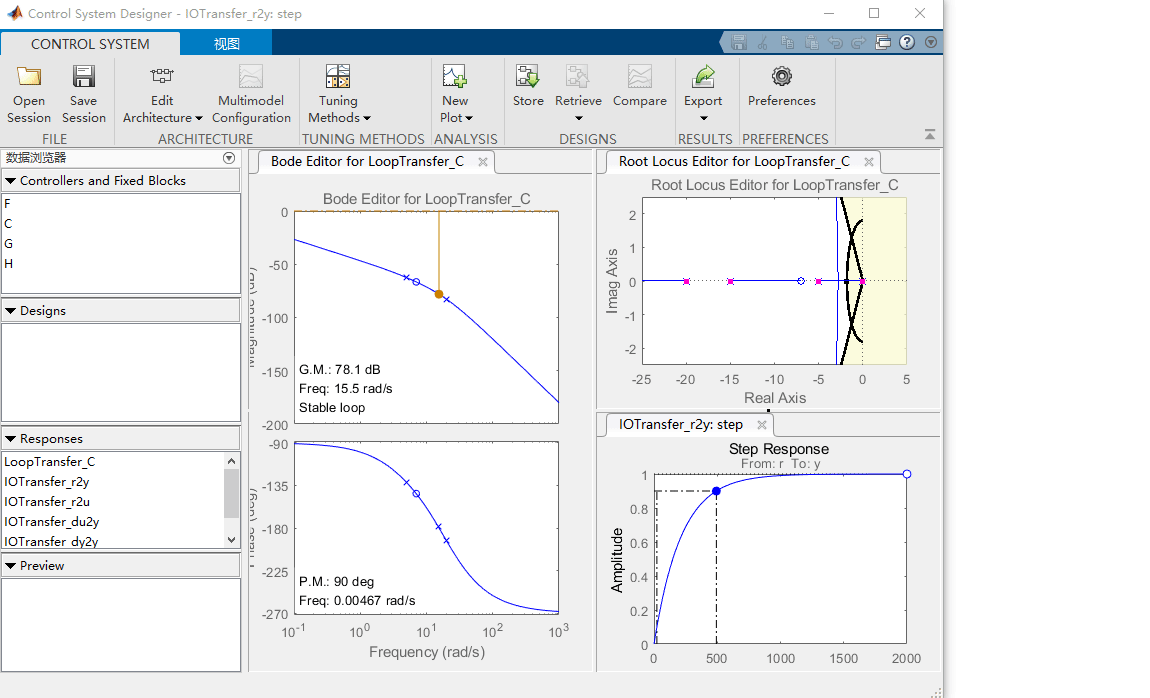
当关闭伯德图后,可以显示为:

正如阶跃响应上的特性所示,过冲是可以接受的,但上升时间太大。根轨迹上的粉红色框显示了当前所选控制增益 K K K 的对应闭环极点位置。
要解决此问题,我们需要为增益 K K K 选择一个新值。类似于我们使用rlocfind命令的方式,可以直接在根轨迹图上更改控制器的增益,单击并将最接近虚轴的粉红色框拖动到我们的根轨迹图的可接受区域,如下所示: