LeetCode刷题笔记(Java)---第301-320题
文章目录
-
-
- 前言
- 笔记导航
- 301. 删除无效的括号
- 303. 区域和检索 - 数组不可变
- 304. 二维区域和检索 - 矩阵不可变
- 306. 累加数
- 307. 区域和检索 - 数组可修改
- 309. 最佳买卖股票时机含冷冻期
- 310. 最小高度树
- 312. 戳气球
- 313. 超级丑数
- 315. 计算右侧小于当前元素的个数
- 316. 去除重复字母
- 318. 最大单词长度乘积
- 319.灯泡开关
-
前言
需要开通vip的题目暂时跳过
笔记导航
点击链接可跳转到所有刷题笔记的导航链接
301. 删除无效的括号
删除最小数量的无效括号,使得输入的字符串有效,返回所有可能的结果。
说明: 输入可能包含了除 ( 和 ) 以外的字符。
-
解答
private HashSet<String> set = new HashSet<>(); int minModify = Integer.MAX_VALUE; public List<String> removeInvalidParentheses(String s) { dfs(s,0,0,0,0,new StringBuilder()); return new ArrayList<String>(set); } public void dfs(String s,int index,int leftCount,int rightCount,int remove,StringBuilder temp){ if(rightCount > leftCount)return; if(index == s.length()){ if(leftCount == rightCount){ if(remove <= minModify){ if(remove < minModify){ set.clear(); minModify = remove; } set.add(temp.toString()); } } return; } char currentChar = s.charAt(index); if(currentChar != ')' && currentChar != '('){ temp.append(currentChar); dfs(s,index+1,leftCount,rightCount,remove,temp); temp.deleteCharAt(temp.length()-1); }else{ dfs(s,index+1,leftCount,rightCount,remove+1,temp); temp.append(currentChar); if(currentChar == '(') dfs(s,index+1,leftCount+1,rightCount,remove,temp); else dfs(s,index+1,leftCount,rightCount+1,remove,temp); temp.deleteCharAt(temp.length()-1); } } -
分析
- 回溯来实现
- 每一层递归有4种情况
- 当前字符不是括号,则直接加到temp中
- 删去当前字符,则表示直接跳过这一字符 不对temp进行修改,删除次数+1;
- 左括号,加入到temp中,leftCount+1
- 右括号,加入到temp中,rightCount+1
- 出口
- 右括号数量大于左括号数量,说明不可能组成符合条件的括号组合,直接剪枝
- 当遍历完了整个字符串 若此时的左右括号数量相等继续往前判断
- 若删除次数小于已经记录的最少删除次数。则将之前的set集合清空,修改最少删除次数。将找到的组合temp加入到set集合中。return
303. 区域和检索 - 数组不可变
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
- 解答
class NumArray {
private int[] sum;
public NumArray(int[] nums) {
sum = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
sum[i + 1] = sum[i] + nums[i];
}
}
public int sumRange(int i, int j) {
return sum[j + 1] - sum[i];
}
}
-
分析
- 得到i-j的和其实就是 0~j的和减去0 ~(i-1)的和
- sum数组为nums长度+1 并且设置sum[0]是为了避免nu ms为[[]]而要添加新的条件判断。
- sum[j+1]就是0~j的和;sum[i]就是0~(i-1)的和
-
提交结果
304. 二维区域和检索 - 矩阵不可变
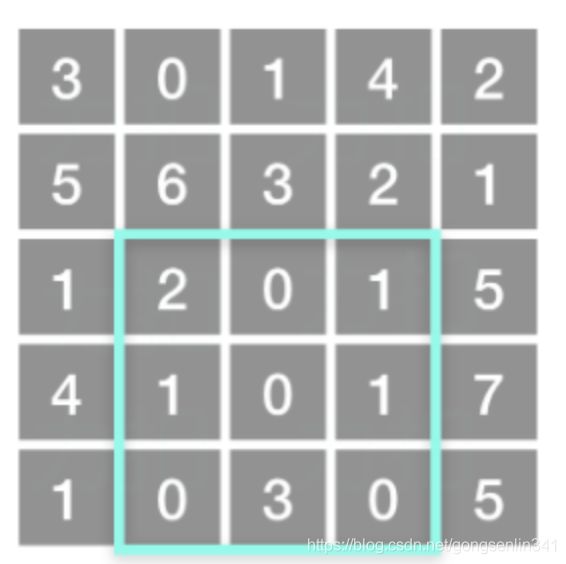
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2)。
上图子矩阵左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = (4, 3),该子矩形内元素的总和为 8。

- 解答
int[][] sum;
public NumMatrix(int[][] matrix) {
if(matrix.length == 0 || matrix[0].length == 0)return;
sum = new int[matrix.length + 1][matrix[0].length + 1];
sum[1][1] = matrix[0][0];
for (int i = 2; i < sum.length; i++) {
sum[i][1] = sum[i - 1][1] + matrix[i - 1][0];
}
for (int i = 2; i < sum[0].length; i++) {
sum[1][i] = sum[1][i - 1] + matrix[0][i - 1];
}
for (int i = 2; i < sum.length; i++) {
for (int j = 2; j < sum[0].length; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
if(row1+1 >= sum.length || row2 >= sum.length || col1 >= sum[0].length || col2 >= sum[0].length)return 0;
return sum[row2 + 1][col2 + 1] - (sum[row1][col2 + 1] + sum[row2 + 1][col1] - sum[row1][col1]);
}
-
分析
- 使用前缀和来做,只是这里时二维的
- sum记录这一位置和左上角构成的四边形内的数字和。
- 给定两个坐标(row1,col1),(row2,col2)
- 两个坐标构成的面积就是[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-evTFvd2b-1597546042630)(/Users/gongsenlin/Library/Application Support/typora-user-images/截屏2020-08-16 上午10.45.06.png)]
306. 累加数
累加数是一个字符串,组成它的数字可以形成累加序列。
一个有效的累加序列必须至少包含 3 个数。除了最开始的两个数以外,字符串中的其他数都等于它之前两个数相加的和。
给定一个只包含数字 ‘0’-‘9’ 的字符串,编写一个算法来判断给定输入是否是累加数。
说明: 累加序列里的数不会以 0 开头,所以不会出现 1, 2, 03 或者 1, 02, 3 的情况。
- 解答
public boolean isAdditiveNumber(String num) {
if (num == null || num.length() < 3)
return false;
return backtrack(0, num, new ArrayList<>());
}
private boolean backtrack(int start, String num, List<String> tmp) {
if (start == num.length() && tmp.size() > 2)
return true;
for (int i = start; i < num.length(); i++) {
String s = num.substring(start, i + 1);
if ((s.length() > 1 && s.charAt(0) == '0'))
return false;
if (s.length() > num.length() / 2) //剪枝
return false;
int size = tmp.size();
if (size < 2 || s.equals(addStrNum(tmp.get(size - 1), tmp.get(size - 2)))) {
tmp.add(s);
if (backtrack(i + 1, num, tmp)) //找到一个结果就返回
return true;
tmp.remove(tmp.size() - 1);
}
}
return false;
}
private static String addStrNum(String a, String b) {
//两数相加
StringBuilder sum = new StringBuilder();
int c = 0; //进位
for (int ai = a.length() - 1, bi = b.length() - 1; ai >= 0 || bi >= 0; ) {
int s = 0;
if (ai >= 0) s += a.charAt(ai--) - '0';
if (bi >= 0) s += b.charAt(bi--) - '0';
sum.append((s + c) % 10);
c = (s + c) >= 10 ? 1 : 0;
}
if (c > 0) sum.append(1);
return sum.reverse().toString();
}
-
分析
- 利用回溯+剪枝实现
- 每轮递归去寻找一个符合条件的子字符串。条件如下
- 开头不能是’0’
- 如果已找到的字符串数量大于等于2的时候,当前的字符串需要等于集合最后两个字符串的和。
- 当前的字符串长度不能大于原字符串的一半,说明两个数相加再加上这个数字的长度已经超出了原字符串。
- 最后若集合中的数量大于2 并且已经遍历到了原字符串的末尾。说明是一个累加序列。返回true
-
提交结果
307. 区域和检索 - 数组可修改
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
update(i, val) 函数可以通过将下标为 i 的数值更新为 val,从而对数列进行修改。
- 解答
//方法一
class NumArray {
int[] dp;
int[] numbers;
int len;
public NumArray(int[] nums) {
numbers = nums;
len = nums.length;
dp = new int[len+1];
if(nums.length == 0)return;
dp[1] = nums[0];
for(int i = 2;i<len+1;i++){
dp[i] = dp[i-1] + nums[i-1];
}
}
public void update(int i, int val) {
for(int j = i;j<len;j++){
dp[j+1] = dp[j+1] - numbers[i] + val;
}
numbers[i] = val;
}
public int sumRange(int i, int j) {
return dp[j+1] - dp[i];
}
}
//方法二
class NumArray {
private int[] nums;
public NumArray(int[] nums) {
this.nums = nums;
}
public int sumRange(int i, int j) {
int sum = 0;
for (int l = i; l <= j; l++) {
sum += nums[l];
}
return sum;
}
public void update(int i, int val) {
nums[i] = val;
}
}
//方法三
class NumArray {
private int[] b;
private int len;
private int[] nums;
public NumArray(int[] nums) {
this.nums = nums;
double l = Math.sqrt(nums.length);
len = (int) Math.ceil(nums.length/l);
b = new int [len];
for (int i = 0; i < nums.length; i++)
b[i / len] += nums[i];
}
public int sumRange(int i, int j) {
int sum = 0;
int startBlock = i / len;
int endBlock = j / len;
if (startBlock == endBlock) {
for (int k = i; k <= j; k++)
sum += nums[k];
} else {
for (int k = i; k <= (startBlock + 1) * len - 1; k++)
sum += nums[k];
for (int k = startBlock + 1; k <= endBlock - 1; k++)
sum += b[k];
for (int k = endBlock * len; k <= j; k++)
sum += nums[k];
}
return sum;
}
public void update(int i, int val) {
int b_l = i / len;
b[b_l] = b[b_l] - nums[i] + val;
nums[i] = val;
}
}
//方法四
class NumArray {
int[] tree;
int n;
public NumArray(int[] nums) {
n = nums.length;
tree = new int[n * 2];
for(int i = n; i < 2*n; i++){
//叶子节点
tree[i] = nums[i-n];
}
for(int i = n-1; i >= 0; i--){
//建树
tree[i] = tree[i*2] + tree[i*2+1];
}
}
public void update(int i, int val) {
int pos = n + i;//找到叶子节点
tree[pos] = val;//叶子节点的值修改
while(pos > 0){
int left = pos%2==0? pos: pos-1;
int right = pos%2==0? pos+1: pos;
tree[pos/2] = tree[left] + tree[right];//修改他的父亲的值
pos /= 2;//指向父亲节点
}
}
public int sumRange(int i, int j) {
int sum = 0;
int l = n + i;//初始化第一个叶子
int r = n + j;//初始化第二个叶子
while(r >= l){
if(l % 2 == 1){
sum += tree[l];
l++;
}
if(r % 2 == 0){
sum += tree[r];
r--;
}
l /= 2;//向上移动一层
r /= 2;//向上移动一层
}
return sum;
}
}
-
分析
- 方法一
- 前缀和求i-j的和
- update更新前缀和
- 方法二
- 每次都计算i-j的和
- 方法三
- 将数组分块 记录下每块内的和。
- 每次更新就找到指定的快,对这个块内和进行更新
- 求i-j的和的时候。根据i和j可以找到是哪几块组成。
- 完整的块直接加b数组中已经求得的和。之外的就根据索引求和。
- 方法四
- 根据二叉树节点在数组中位置的特点来用数组存储二叉树
- 假设有一个结点i 那么它的孩子存储在数组中的位置就是2i 和2i+1
- 更新操作其实就是自底向上的更新结点 以及包含这个节点的父亲节点。
- 取值也是从叶子节点开始,逐步向上移动来计算和值。
-
提交结果
方法二
方法三
方法四
309. 最佳买卖股票时机含冷冻期
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
- 解答
public int maxProfit(int[] prices) {
int days = prices.length;
if(days==0||days == 1)return 0;
int[][] dp = new int[days][3];
dp[0][0] = -prices[0];
for(int i = 1;i<days;i++){
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][2]-prices[i]);
dp[i][1] = dp[i-1][0] + prices[i];
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]);
}
return Math.max(dp[days-1][0],Math.max(dp[days-1][1],dp[days-1][2]));
}
-
分析
-
dp[i] [j]表示第i天结束后的状态j下的最大利润。
-
状态分为三种
- 持有股票
- 不持有股票处于冷冻期
- 不持有股票不处于冷冻期
-
状态转移方程如下
-
dp[i] [0]表示第i天结束后持有股票 持有股票可以分为两种情况 第一种是第i天没有买入股票 保持的是第i-1天买入的股票;第二种是第i-1天不持有股票且处于冷冻期,第i天买入股票。所以可以列出如下的动态转移方程
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][2]-prices[i]); -
dp[i] [1]表示第i天结束后不持有股票且处于冷冻期。表示i-1天持有股票,第i天卖出,所以可以列出如下的动态转移方程
dp[i][1] = dp[i-1][0] + prices[i]; -
dp[i] [2]表示第i天结束后不持有股票且不处于冷冻期。分为两种情况。第一种 第i-1天不持有股票处于冷冻期;第二种第i-1天不持有股票且不处于冷冻期。所以可以列出如下的动态转移方程
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]);
-
-
最后返回最后一天结束后 3种状态中的最大值。
-
310. 最小高度树
对于一个具有树特征的无向图,我们可选择任何一个节点作为根。图因此可以成为树,在所有可能的树中,具有最小高度的树被称为最小高度树。给出这样的一个图,写出一个函数找到所有的最小高度树并返回他们的根节点。
格式
该图包含 n 个节点,标记为 0 到 n - 1。给定数字 n 和一个无向边 edges 列表(每一个边都是一对标签)。
你可以假设没有重复的边会出现在 edges 中。由于所有的边都是无向边, [0, 1]和 [1, 0] 是相同的,因此不会同时出现在 edges 里。
说明:
根据树的定义,树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。
树的高度是指根节点和叶子节点之间最长向下路径上边的数量。
-
解答
public List<Integer> findMinHeightTrees(int n, int[][] edges) { List<Integer> res = new ArrayList<>(); if (n == 1) { res.add(0); return res; } int[] degree = new int[n]; List<List<Integer>> map = new ArrayList<>(); for (int i = 0; i < n; i++) { map.add(new ArrayList<>()); } for (int[] edge : edges) { degree[edge[0]]++; degree[edge[1]]++; map.get(edge[0]).add(edge[1]); map.get(edge[1]).add(edge[0]); } Queue<Integer> queue = new LinkedList<>(); for (int i = 0; i < n; i++) { if (degree[i] == 1) queue.offer(i); } while (!queue.isEmpty()) { res = new ArrayList<>(); int size = queue.size(); for (int i = 0; i < size; i++) { int cur = queue.poll(); res.add(cur); List<Integer> neighbors = map.get(cur); for (int neighbor : neighbors) { degree[neighbor]--; if (degree[neighbor] == 1) { queue.offer(neighbor); } } } } return res; } -
分析
- 首先计算图中所有结点的度
- 记录下所有结点和他对应的邻居
- 将度为1的点入队。
- while循环
- 队中的元素出队,加入到这一次循环的答案集合中,邻居的度减1
- 当度为1的时候入队。
- 直到队空。此时res记录的就是可以作为根的结点。
- 层层包围。每层while循环就是去掉最外层。
- 这样最后记录在res中的就是最中间的结点。这些结点作为根可以得到最矮的树。树高也就是这个点到最外圈的最大距离。
312. 戳气球
有 n 个气球,编号为0 到 n-1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。如果你戳破气球 i ,就可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后,气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。
- 解答
public int maxCoins(int[] nums) {
int n = nums.length;
int[] points = new int[n + 2];
points[0] = points[n + 1] = 1;
for (int i = 1; i <= n; i++) {
points[i] = nums[i - 1];
}
int[][] dp = new int[n + 2][n + 2];
for (int i = n; i >= 0; i--) {
for (int j = i + 2; j < n + 2; j++) {
for (int k = i + 1; k < j; k++) {
dp[i][j] = Math.max(
dp[i][j],
dp[i][k] + dp[k][j] + points[i]*points[j]*points[k]
);
}
}
}
return dp[0][n + 1];
}
-
分析
- 为了方便操作 左右两边各加上一个1
- 使用动态规划
- dp[i] [j]表示 i~j的范围内可以获得最多的银币。i 和j不戳破!刚好左右两边的1 是辅助用的 不可戳破
- 阶段划分 i~j的范围内 选择一个点k 这个点最为最后戳破的点。这样就可以将i~j划分成i~k和k~j。
- dp[i] [k]表示i和k不戳破的情况下 范围内的最多金币
- dp[k] [j]表示k和j不戳破的情况下 范围内的最多金币。
- 其余的气球都戳破了 就剩下了i和j还有k没有戳破
- k是最后一个戳破的 所以戳破k可以得到points[i]✖️points[j]✖️points[k]个金币。
- 而这个k是要枚举的。i~j中选择一个点作为k 这样从这个枚举的结果中选择结果最多的即可
- 所以动态转移方程可以列为
- dp[i] [j] = Math.max(dp[i] [k] + dp[k] [j] + points[i]✖️points[j]✖️points[k]);
- 自底向上 从小范围到大范围 也就是从子问题到原问题的顺序 计算dp
- 最后返回dp[0] [n+1]即为答案。
-
313. 超级丑数
编写一段程序来查找第 n 个超级丑数。
超级丑数是指其所有质因数都是长度为 k 的质数列表 primes 中的正整数。
-
解答
public int nthSuperUglyNumber(int n, int[] primes) { int[] dp = new int[n]; dp[0] = 1; int[] indexs = new int[primes.length]; for(int i = 0;i< n - 1;i++){ int min = Integer.MAX_VALUE; for(int j = 0;j<primes.length;j++){ if(min > primes[j] * dp[indexs[j]]) min = primes[j] * dp[indexs[j]]; } for (int j = 0; j < primes.length; j++) { if(min == primes[j] * dp[indexs[j]]) indexs[j]++; } dp[i+1] = min; } return dp[n-1]; } -
分析
- 和找第n个丑数差不多 只是这里 丑数的质因数不止2,3,5.原来是用3个指针来表示下一个匹配的位置。
- 现在是k个质因数 所以需要一个长度为k的数组 来表示下一个要计算的数字的位置。
- dp[0] 初始化为1
- Primes 中的每一个数乘以dp[0]。所有的结果中选择最小的一个 最为dp[1]的值。并且把Primes中这个质因数对应记录索引位置+1 表示这一位质因数下次要✖️的位置。
- 如果出现了不同的质因数✖️以dp中的结果得到的最小值是一样的 那么这几个质因数所对应的索引数组的位置都加1
- 最后返回dp[n-1]即可
315. 计算右侧小于当前元素的个数
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
- 解答
public List<Integer> countSmaller(int[] nums) {
TreeSet<Integer> set = new TreeSet<>();
for (int i = 0; i < nums.length; i++) {
set.add(nums[i]);
}
int[] numbers = new int[set.size() + 1];
int index = 1;
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : set) {
map.put(num, index++);
}
LinkedList<Integer> res = new LinkedList<>();
for (int i = nums.length - 1; i >= 0; i--) {
Integer ind = map.get(nums[i]);
res.addFirst(numbers[ind - 1]);
for (int j = ind; j < numbers.length; j++) {
numbers[j]++;
}
}
return res;
}
//方法二
public List<Integer> countSmaller(int[] nums) {
List<Integer> result = new ArrayList<>();
int len = nums.length;
if (len == 0) {
return result;
}
int[] indexes = new int[len];
int[] temp = new int[len];
int[] res = new int[len];
for (int i = 0; i < len; i++) {
indexes[i] = i;
}
mergeAndCountSmaller(nums, 0, len - 1, indexes, temp, res);
for (int i = 0; i < len; i++) {
result.add(res[i]);
}
return result;
}
// 归并排序
private void mergeAndCountSmaller(int[] nums, int left, int right, int[] indexes, int[] temp, int[] res) {
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
//拆分
mergeAndCountSmaller(nums, left, mid, indexes, temp, res);
mergeAndCountSmaller(nums, mid + 1, right, indexes, temp, res);
// 归并排序的优化。如果索引数组有序,则不存在逆序关系,没有必要合并。
if (nums[indexes[mid]] <= nums[indexes[mid + 1]]) {
return;
}
//合并
mergeOfTwoSortedArrAndCountSmaller(nums, left, mid, right, indexes, temp, res);
}
private void mergeOfTwoSortedArrAndCountSmaller(int[] nums, int left, int mid, int right, int[] indexes, int[] temp, int[] res) {
for (int i = left; i <= right; i++) {
temp[i] = indexes[i];//记录下索引改变前的状态
}
int i = left;
int j = mid + 1;
for (int k = left; k <= right; k++) {
if (i > mid) {
//前一部分数组以归并 第二个数组直接接在后面即可。
indexes[k] = temp[j];
j++;
} else if (j > right) {
//后一个部分的数组以归并,第一个数组接在后面即可。此时要计算逆序对
indexes[k] = temp[i];
i++;
res[indexes[k]] += (right - mid);
} else if (nums[temp[i]] <= nums[temp[j]]) {
// 前一数组中的小于第二个数组中的 小的归并 计算逆序对
indexes[k] = temp[i];
i++;
res[indexes[k]] += (j - mid - 1);
}else {
// 后面的值大
indexes[k] = temp[j];
j++;
}
}
}
-
分析
- 首先记录下nums数组中出现的数字。
- 按大小 从小到大保存在一个数组numbers中。
- 从后往前遍历。找到numbers数组中这个数字对应的下标。这个位置包括之后的位置的值+1。 表示出现了比这个位置的值小的数。
- 而遍历的当前位置 后有多少个比它小的数 就看numbers数组中 这个数字对应下标的前一位的值。
例如 nums数组中有这几个数字 然后从小到大的排列。
从后往前遍历。数字是3 那么3 对应的位置极其之后的桶都加1。
这个位置之后有多少个比它小的数 就看这个数字的桶的前一个桶的数字是多少即可。
以此类推
-
方法二
归并排序+索引数组来寻找逆序对。
在合并的时候 计算逆序对。
316. 去除重复字母
给你一个仅包含小写字母的字符串,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
-
解答
public static String removeDuplicateLetters(String s) { HashMap<Character, Integer> map = new HashMap<>(); for (int i = 0; i < s.length(); i++) { map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1); } LinkedList<Character> linkedList = new LinkedList<>(); Set<Character> set = new HashSet<>(); for (int i = 0; i < s.length(); i++) { int size = linkedList.size(); char current = s.charAt(i); if (!set.contains(current)) { while (size > 0) { char number = linkedList.getLast(); if (current < number && map.get(number) > 0) { linkedList.removeLast(); set.remove(number); size--; } else break; } linkedList.addLast(current); set.add(current); } map.put(current, map.get(current) - 1); } StringBuilder stringBuilder = new StringBuilder(); while (linkedList.size() > 0) stringBuilder.append(linkedList.pop()); return stringBuilder.toString(); } -
分析
- 首先用hashmap记录每一个字母出现的次数
- 用一个队列来记录遍历的最小字典序
- 遍历字符串。
- 若当前字符已经出现在队列中 不入队
- 否则,当前字符比队尾字符小的时候 并且队尾的字符在之后还会出现。那么先将队尾字符出队。再入队。
- 每一轮遍历 将map字母计数-1
- 最后队中的序列就是最小字典序。
-
提交结果
318. 最大单词长度乘积
给定一个字符串数组 words,找到 length(word[i]) * length(word[j]) 的最大值,并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词,返回 0。

-
解答
public int maxProduct(String[] strings) { int n = strings.length; int[] masks = new int[n]; int[] lens = new int[n]; int bitmask = 0; for (int i = 0; i < n; i++) { bitmask = 0; for (char ch : strings[i].toCharArray()) { bitmask |= 1 << bitNumber(ch); } masks[i] = bitmask; lens[i] = strings[i].length(); } int max = 0; for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { if ((masks[i] & masks[j]) == 0) max = Math.max(max, lens[i] * lens[j]); } } return max; } public int bitNumber(char ch) { return (int) ch - (int) 'a'; } -
分析
- 比较两个单词的长度可以用位运算。26个字母对应26位。出现的字母 在对应位置上设1.这样比较两个单词是否包含相同字母 只要两个转换后的数做与运算即可。这样比较两个单词的时间复杂度为两个单词的长度相加。比单纯的一个一个字母比较O(n平方)要快。
- 用数组提前保留转换后的数。这样可以减少计算的次数。
- 然后就是两个for循环来比较得到最大的解。
319.灯泡开关
初始时有 n 个灯泡关闭。 第 1 轮,你打开所有的灯泡。 第 2 轮,每两个灯泡你关闭一次。 第 3 轮,每三个灯泡切换一次开关(如果关闭则开启,如果开启则关闭)。第 i 轮,每 i 个灯泡切换一次开关。 对于第 n 轮,你只切换最后一个灯泡的开关。 找出 n 轮后有多少个亮着的灯泡。
-
解答
//超时 public int bulbSwitch(int n) { int[] dp = new int[n + 1]; for (int i = 1; i <= n; i++) { dp[i] = 1; } int res = 0; for (int i = 2; i <= n / 2; i++) { int j = n / i; for (int k = 1; k <= j && k * i <= n; k++) { dp[k * i] = ~dp[k * i]; if (k == 1 && dp[k * i] == 1) res++; } } for (int i = n / 2 + 1; i <= n; i++) { dp[i] = ~dp[i]; if (dp[i] == 1) res++; } return res + 1; } public int bulbSwitch(int n) { return (int)Math.sqrt(n); } -
分析
- 一开始按部就班写的算法超时。
- 后来考虑到判断一个灯泡是否亮着。主要就看他被操作了多少次。奇数次是亮着,偶数次是灭的。
- 而第i个灯泡什么时候会被操作呢。在i的因数的轮次的时候 会被操作。
- 例如10 因数1,2,5,10 在这4轮的时候灯泡会被操作
- 例如20 因数1,2,4,5,10,20 在这6轮会被操作。
- 所以这个问题就演变成了 哪些灯泡被操作的次数是奇数次。
- 可以发现因数是偶数的灯泡被操作了偶数次。那么哪些数的因数是奇数呢。答案是完全平方数。因为因数是成对出现的。只有完全平方数会出现两个一样的因数。所以是奇数。
- 就是求n个灯泡中 有多少个完全平方数。