并查集

（我第一次写博客，写的有不对之处，敬请斧正。）

参考了部分《算法竞赛进阶指南》。（挺好的书）

我一直觉得并查集是一种很好用、基础的数据结构，比如在kruskal算法、判断欧拉回路（无序字母对）、有向图中寻找最小环（信息传递），最近一直在用到并查集，但感觉自己并没有理解的很到位，就再看了一遍，写下这篇博客，希望能帮助有需要的人更好地理解。

定义

动态维护若干个不重叠的集合，并支持合并与查找。

实现

使用一个树形结构存储每个集合，每个节点代表一个元素，根节点是该集合的代表。整个并查集就是森林。
下面给出朴素版的代码（思路较为简单，此处不再赘述）

int fa[N];

for (int i = 1; i <= n; i ++ ) fa[i] = i;//即有n棵一个节点的树。

int get(int x){
     
	if (x == fa[x]) return x;
	return get(fa[x]);
}

void merge(int x, int y){
     
	fa[x] = y;
}

路径压缩与按秩合并

路径压缩：因为我们只关心树形结构的根节点，并不关心树的形态。所以我们可以在每次get操作时，把访问过的节点都指向根节点。每次get操作时间复杂度为O（logN）。

按秩合并：（秩既可指集合大小，也可指树的深度）在合并时把秩小的树根作为秩大的树根的子节点。每次get操作时间复杂度为O(logN)。

一般我们只需用上路径压缩即可。

//附上代码
int fa[N];

for (int i = 1; i <= n; i ++ ) fa[i] = i;

int get(int x){
     
	if (x == fa[x]) return x;
	return fa[x] = get(fa[x]);
}

void merge(int x, int y){
     
	fa[get(x)] = get(y);
}

1. 动态维护具有传递性的关系。（就像平行线的传递）
2. 维护一个数组中位置的占用情况（还记得第一次写supermarket时，每次都从该商品的过期时间d开始往前循环看哪天是空的。但用并查集：每个位置所在集合的代表就是从它开始往前数第一个空闲的位置，可以快速地查询。）

扩展域与边带权的并查集

例题：银河英雄传说

当指令为C时，表示询问第 i 号和 j 号战舰是否在同一列，若在同一列，它们之间间隔多少战舰。
此时我们就需要d数组来记录信息。每次get操作时更新d数组

int get(int x){
     
	if (x == fa[x]) return ;
	int root = get(fa[x]);//找出集合代表
	d[x] += d[fa[x]];//从x到树根的路径上的所有边权之和
	return fa[x] = root;
}

当指令为M时，表示把第 x 列的战舰接到第 y 列的尾部，即把 x 的树根作为 y 的树根的子节点。
此时d[x] = 未合并前 y 集合的大小，所以需要一个size数组记录集合大小

void merge(int x, int y){
     
	x = get(x), y = get(y);
	fa[x] = y, d[x] = size[y];
	size[y] += size[x];
}

例题：奇偶游戏

（好蓝，>大哭<）
我第一遍看完题目压根没想到并查集。

首先，根据程序自动分析可知，并查集可以动态维护传递性的关系，只需找出本题的传递关系：

[l，r]中有奇数个1 <==> [1，l-1] 与[1，r]奇偶性不同

[l，r]中有偶数个1 <==> [1，l-1] 与[1，r]奇偶性相同

1. 若a、b奇偶性相同，b、c奇偶性相同，那么a、c奇偶性相同
2. 若a、b奇偶性不同，b、c奇偶性相同，那么a、c奇偶性不同
3. 若a、b奇偶性不同，b、c奇偶性不同，那么a、c奇偶性相同

为了处理本题多种传递关系，我们使用边代权的并查集。
d[x] = 0 表示 fa[x] 与 d[x] 奇偶性相同；d[x] = 1 表示 fa[x] 与 d[x] 奇偶性不同。
在路径压缩时，对x到树根路径上的所有边做异或操作，就可以得到x与树根的奇偶性关系。

那么现在对于[l，r]，设ans表示该问题的答案。
先检查 l 和 r 是否在同一个集合内（奇偶关系是否已知）。
若在同一个集合内： l = get ( l )，r = get( r )，若d[l] xor d[r] != ans，即可确定小A撒谎。
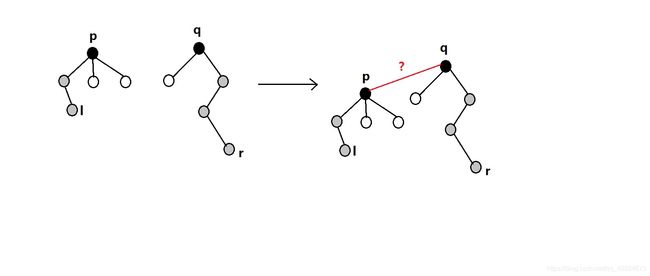
若不在同一个集合内：合并两个集合，得到两个集合的树根 p、q，令 p 为 q 的子节点，那么 l 与 r 的奇偶性关系ans = d[l] xor d[r] xor d[p]，所以d[p] = d[l] xor d[r] xor ans。

还有一点就是N比较大，fa和d数组开不出来，易想到离散化，把 l 、r 缩到2M的范围内。

#include<bits/stdc++.h>
using namespace std;
const int M = 10000 + 5;
int n, m, a[2 * M], fa[2 * M], d[2 * M];
struct node{
     
    int l, r, ans;
}qu[M];
int get(int x){
     
    if(x == fa[x]) return x;
    int rt = get(fa[x]); d[x] ^= d[fa[x]];
    return fa[x] = rt;
}
int main()
{
     
    scanf("%d%d", &n, &m);
    //离散化
    for (int i = 1; i <= m; i ++ ){
     
        char c[5];
        scanf("%d%d%s", &qu[i].l, &qu[i].r, c);
        qu[i].ans = (c[0] == 'o'?1:0);
        a[2 * i - 1] = qu[i].l - 1, a[2 * i] = qu[i].r;
    }
    sort(a + 1, a + 2 * m + 1);
    n = unique(a + 1, a + 2 * m + 1) - (a + 1);//去重
    
    for (int i = 1; i <= n; i ++ ) fa[i] = i;
    for (int i = 1; i <= m; i ++ ){
     
        //求出l-1和r离散化后的值
        int x = lower_bound(a + 1, a + n + 1,qu[i].l - 1) - a;
        int y = lower_bound(a + 1, a + n + 1,qu[i].r - 1) - a;
        int p = get(x), q = get(y);
        if (p == q) {
     //若在同一个集合内
            if((d[x] ^ d[y]) != qu[i].ans)
            {
     printf("%d\n", i - 1); return 0;}
        }
        else 
            fa[p] = q,d[p] = d[x] ^ d[y] ^ qu[i].ans;
    }
    printf("%d\n",m);
    return 0;
}

扩展域的并查集（直接附代码）

int get(int x){
     
	if(x == fa[x]) return fa[x];
	return fa[x] = get(fa[x]);
}
for (int i = 1; i <= 2 * n; i ++ ) fa[i] = i;
    for (int i = 1; i <= m; i ++ ){
     
        //求出l-1和r离散化后的值
        int x = lower_bound(a + 1, a + n + 1,qu[i].l - 1) - a;
        int y = lower_bound(a + 1, a + n + 1,qu[i].r - 1) - a;
        int x_odd = x, x_even = x + n; //一个变量拆成两个节点 
        int y_odd = y, y_even = y + n;
        if (!qu[i].ans) {
     //奇偶性相同 
            if(get(x_odd) == get(y_even)) {
     printf("%d\n", i - 1); return 0;}
            fa[get(x_odd)] = get(y_odd);
            fa[get(x_even)] = get(y_even);
        }
        else {
     //奇偶性不同 
        	if(get(x_odd) == get(y_odd)){
     printf("%d\n", i - 1); return 0;}//矛盾
			fa[get(x_odd)] = get(y_even);
			fa[get(x_even)] = get(y_odd); 
		}
    }
    printf("%d\n",m);

例题：食物链

我感觉扩展域并查集更容易理解：
把每个动物拆分成3个节点：同类域x_self，捕食域x_eat，天敌域x_enemy。
若 x 与 y 是同类，合并x_self与 y_self， x_eat与 y_eat， x_enemy与 y_enemy。
若 x 吃 y ， 合并x_eat与y_self，x_self与y_enemy，x_enemy与y_eat。

#include <bits/stdc++.h>
using namespace std;
int n, k, ans, fa[150000 + 5];
int get(int x){
     
	if (x == fa[x]) return x;
	return fa[x] = get(fa[x]);
} 
int main() {
     
	scanf("%d%d", &n, &k);
	for (int i = 1; i <= 3 * n; i ++ ) fa[i] = i;
	for (int i = 1; i <= k; i ++ ){
     
		int z, x, y; scanf("%d%d%d", &z, &x, &y);
		if(x > n || y > n ) {
     ans ++;continue;}
		int x_self = x, x_eat = x + n, x_enemy = x + 2 * n;
		int y_self = y, y_eat = y + n, y_enemy = y + 2 * n;
		int x1 = get(x_self), x2 = get(x_eat), x3 = get(x_enemy);
		int y1 = get(y_self), y2 = get(y_eat), y3 = get(y_enemy);
		if (z == 1){
     
			if (x1 == y2 || x1 == y3 ) {
     ans ++; continue;}
			fa[x1] = y1; fa[x2] = y2; fa[x3] = y3;
		}
		else {
     
			if (x1 == y1 || x1 == y2 || x == y) {
     ans ++; continue;}
			fa[x1] = y3; fa[x2] = y1; fa[x3] = y2;
		}
	}
	printf("%d\n", ans);
	return 0;
}

可持久化并查集

这是道好（难）题，可以试一试。