P1036 选数（DFS）

题目传送门

题目

已知 $n$ 个整数 $x_1,x_2,\dots ,x_n$，以及 $1$ 个整数$k(k<n)$。从$n$个整数中任选$k$个整数相加，可分别得到一系列的和。例如当$n=4,k=3,4$个整数分别为$3,7,12,19$时，可得全部的组合与它们的和为：

$$\begin{gathered} 3+7+12=22 \\ 3+7+19=29 \\ 7+12+19=38 \\ 3+12+19=34 \end{gathered}$$。

现在，要求你计算出和为素数共有多少种。

例如上例，只有一种的和为素数：$3+7+19=29$。

输入格式

$$\begin{gathered} n,k \\ {x}_1,x_2,\dots ,x_n \end{gathered}$$

输出格式

屏幕输出，格式为： $1$ 个整数（满足条件的种数）。

数据范围

$$\begin{gathered} (1\le n\le 20,k<n) \\ (1\le x_i\le 5000000) \end{gathered}$$

输入输出样例

样例输入1

4 3
3 7 12 19

样例输出1

1

思路

DFS。通过DFS暴力搜索出所有$n$个整数中任选$k$个整数的情况。我们以升序的顺序搜索，保证选数的不重复。
以下是样例的搜索流程：

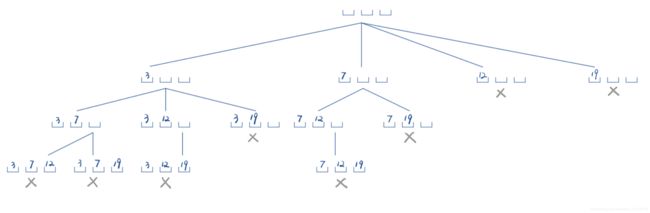
判断素数的朴素方法：

bool ifPrime(int u) {
     
	int m = (int)sqrt(u);
	for(int i = 2; i <= m; i++)
		if(u % i == 0) return false;
	return true;
}

代码

#include
#include
#include

using namespace std;

const int N = 50;

int n, k, res, c;
int x[N];

bool ifPrime(int u) {
     
	int m = (int)sqrt(u);
	for(int i = 2; i <= m; i++)
		if(u % i == 0) return false;
	return true;
}

void dfs(int s, int res, int u)
{
     
    if(u == k)
    {
     
        if(ifPrime(res)) c++;
        return;
    }
    for(int i = s; i < n; i++)
        dfs(i + 1, res + x[i], u + 1);
}

int main()
{
     
    cin >> n >> k;
    for(int i = 0; i < n; i++) scanf("%d", &x[i]);
    dfs(0, 0, 0);
    printf("%d", c);
    return 0;
}