阿里云天池零基础入门CV赛事(7)——模型集成(dropout)
上次听完安晟大神的讲解,将测试集中图像的尺寸设置为了(60, 120),再次运行baseline,将epochs设置为了15次,以下是训练集和验证集的损失函数值。
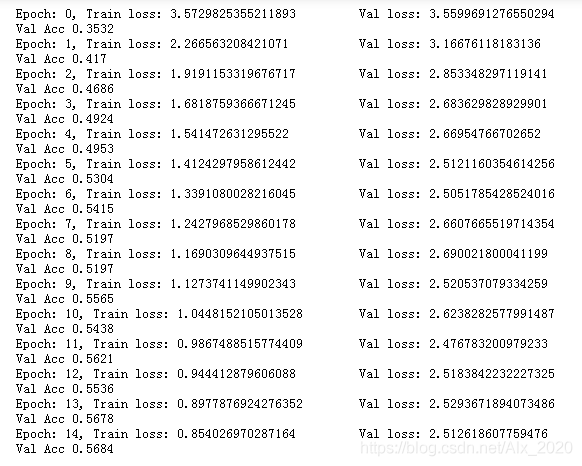
使用matplotlib绘制出曲线图:
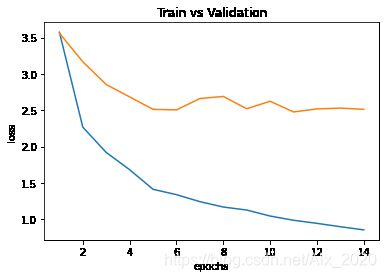
在上图中可以看出训练集的损失函数值是在不断的下降,而验证集的损失函数值在第七次时出现了上升, 而且到后面不出现下降,说明该模型出现的过拟合。
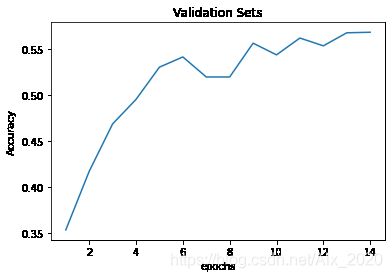
上一篇也说了处理过拟合的方法,这次详细介绍一下dropout方法。
Dropout是广泛应用于深度学习的正则化技术。它会在每次迭代中随机关闭一些神经元。
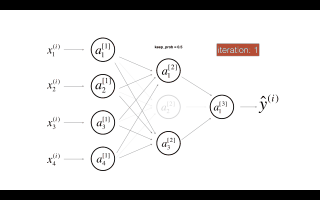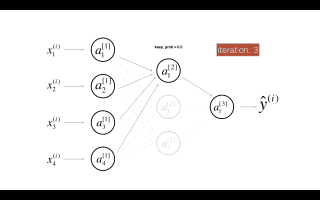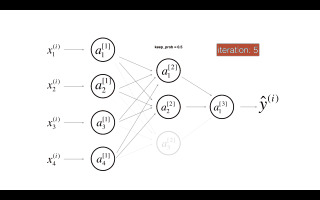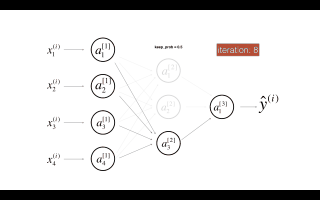
dropout第二个隐藏层。在每次迭代中,以概率1 - keep_prob或以概率keep_prob(此处为50%)关闭此层的每个神经元。关闭的神经元对迭代的正向和反向传播均无助于训练。
1 带有Dropout的正向传播
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation:LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID
Args:
X: -- input dataset, of shape (2, number of examples)
parameters: -- python dictionary containing your parameters W1, b1, W2, b2, W3, b3
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (3, 1)
b3 -- bias vector of shape (1, 1)
keep_prob: -- probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape(1, 1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
# LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# Steps 1-4 below correspond to the Steps 1-4 described above.
D1 = np.random.rand(A1.shape[0], A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand()
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1 * D1 # Step 3: shut down some neuron of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0], A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand()
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = A2 * D2 # Step 3: shut down some neuron of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
2 带有Dropout的反向传播
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout
Args:
X: -- input dataset, of shape (2, number of examples)
Y: -- "true" labels vector, of shape (output size, number of examples)
cache: -- cache output from forward_propagation_with_dropout()
keep_prob: -- probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ3, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {
'dZ3': dZ3, 'dW3': dW3, 'db3': db3, 'dA2': dA2,
'dZ2': dZ2, 'dW2': dW2, 'db2': db2, 'dA1': dA1,
'dZ1': dZ1, 'dW1': dW1, 'db1': db1}
return gradients
参考
吴恩达——深度学习
吴恩达深度学习练习题.
总有一个遗忘的过程,记录一下为以后查找方便。