图的存储结构——邻接多重表(多重邻接表)的实现
7.2 图的存储结构
- 7.2.3 邻接多重表(多重邻接表)Adjacency Multilist
-
- 邻接多重表的类定义
-
- 邻接多重表的顶点结点类模板
- 邻接多重表的边结点类模板
- 邻接多重表的类模板
- 邻接多重表与邻接表的对比
7.2.3 邻接多重表(多重邻接表)Adjacency Multilist
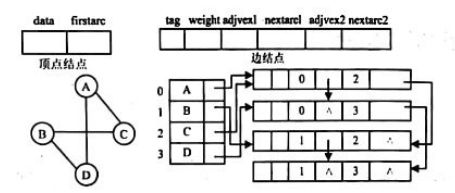
在无向图的邻接表中可以看到,每一条边(vi,vj)在邻接表中有两个边结点:一个在顶点vi的边链表中,表示(vi,vj);一个在顶点vj的边链表中,表示(vj,vi)。
在较复杂的问题中,有时需要给被处理的边加标记(如访问标志或删除标志等),若用邻接表表示,则需要同时给表示某一条边的两个边结点加标记,而这两个结点又不在同一个边链表中,所以处理会很不方便。若改用邻接多重表作为无向图的存储表示,则可简化上述问题的处理。
邻接多重表的类定义
邻接多重表的顶点结点类模板
对图中的每一个顶点用一个顶点结点表示,它有两个域组成,其中:
data域存储有关顶点的信息;
firstarc域是链接指针,指向第一条依附于该顶点的边。
所有的顶点结点组成一个顺序表。
template <class ElemType ,class WeightType>
class MultiAdjListNetworkVex
{
public:
ElemType data;
MultiAdjListNetworkArc<WeightType> *firstarc;
MultiAdjListNetworkVex()
{
firstarc = NULL;
}
MultiAdjListNetworkVex(ElemType val, MultiAdjListNetworkArc<WeightType>* adj = NULL)
{
data = val;
firstarc = adj;
}
};
邻接多重表的边结点类模板
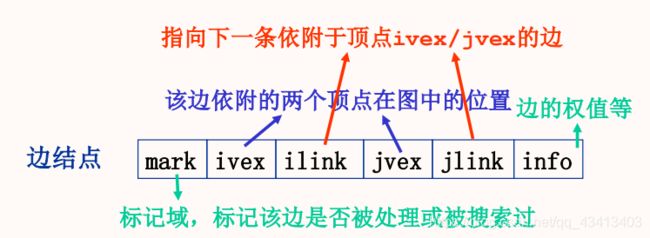
在无向图的邻接多重表中,图的每一条边用一个边结点表示,它由六个域组成,其中:
tag是标记域,标记该边是否被处理或被搜索过;
weight为边的信息域,用于存储边的权值;adjvexl和adjvex2是顶点域,表示该边所依附的两个顶点在图中的序号;
nextarcl1域是链接指针,指向下一条依附于顶点adjvexl的边;
nextarc2也是链接指针,指向下一条依附于顶点adjvex2的边。
template <class WeightType>
class MultiAdjListNetworkArc
{
public:
int mark; //标记该边是否被搜索或处理过
WeightType weight; //边的权重
int adjVex1; //边的一个顶点
MultiAdjListNetworkArc<WeightType>* nextarc1; //指向下一条依附于adjvex1的边,eg:1-2-->1-3-->5-1
int adjVex2;
MultiAdjListNetworkArc<WeightType>* nextarc2;
MultiAdjListNetworkArc()
{
adjVex1= -1;
adjVex2= -1;
}
MultiAdjListNetworkArc(int v1, int v2, WeightType w, MultiAdjListNetworkArc<WeightType>* next1 = NULL,MultiAdjListNetworkArc<WeightType>* next2 = NULL)
{
adjVex1 = v1; adjVex2 = v2;
weight = w;
nextarc1 = next1; nextarc2=next2;
mark = 0; //0表示未被搜索,1表示被搜索过
}
邻接多重表的类模板
1.类定义
template <class ElemType,class WeightType>
class MultiAdjListNetwork
{
protected:
int vexNum, vexMaxNum, arcNum;
MultiAdjListNetworkVex<ElemType, WeightType>* vexTable;
int* tag;
WeightType infinity;
public:
MultiAdjListNetwork(ElemType es[], int vertexNum,int vertexMaxNum= DEFAULT_SIZE, WeightType infinit = (WeightType)DEFAULT_INFINITY);
MultiAdjListNetwork(int vertexMaxNum = DEFAULT_SIZE, WeightType infinit = (WeightType)DEFAULT_INFINITY);
void Clear();
bool IsEmpty()
{
return vexNum == 0;
}
int GetArcNum()const
{
return arcNum;
}
int GetvexNum()const
{
return vexNum;
}
int FirstAdjVex(int v)const;
int NextAdjVex(int v1, int v2)const;
MultiAdjListNetworkArc<WeightType>* NextArc(int v1,MultiAdjListNetworkArc<WeightType>*p)const;
MultiAdjListNetworkArc<WeightType>* LastArc(int v1,MultiAdjListNetworkArc<WeightType>*p)const;
void InsertVex(const ElemType& d);
void InsertArc(int v1, int v2, WeightType w);
void DeleteVex(const ElemType& d);
void DeleteArc(int v1, int v2);
MultiAdjListNetwork(const MultiAdjListNetwork<ElemType, WeightType>* copy);
MultiAdjListNetwork<ElemType, WeightType> &operator=(const MultiAdjListNetwork<ElemType, WeightType>& copy);
///深度优先遍历
void DFS1(const int v);
void DFS1Traverse();
void DFS2();
int GetAdjVex(int head,int pre);//从顶点v出发的一个顶点u,返回v通往的下一个顶点;如果没有其它分支或者已经是最后一个连通点,返回-1;如果要取第一个顶点传入-1
void DFS3();
void BFS();
void Show();
};
2.函数的实现
研讨题,能够运行,但是代码不一定是最优的。
#include
}
if(!s.empty())
{
tmp=s.top();
s.pop();
q=vexTable[tmp].firstarc;
int t=tmp;
while(q&&tag[tmp]!=0)
{
tmp=(q->adjVex1==t?q->adjVex2:q->adjVex1);
//cout<<" 2nd tmp="<
q=NextArc(t,q);
}
if(tag[tmp]==0)
s.push(t);
///1、对应上面连通分支只有1个点的情况
///2、t上的点都被访问过,此时tmp是t相连的最后一个点,用于跳过上面while,再次进行出栈
///tmp要么等于找到的第一个未访问节点,
///要么等于与t相连最后一个点(已被访问过)
///当连通图只有一个节点时,这时tmp=这个已访问的孤立节点
}
}
}
}
//从顶点v出发的一个顶点u,返回v通往的下一个顶点;如果没有其它分支或者已经是最后一个连通点,返回-1;如果要取第一个顶点传入-1
template<class ElemType, class WeightType> int
MultiAdjListNetwork<ElemType, WeightType>::GetAdjVex(int head,int pre)
{
if(head==pre)
return -1;
MultiAdjListNetworkArc<WeightType> *p;
p=vexTable[head].firstarc;
if(pre==-1&&p!=NULL)
return p->adjVex1==head?p->adjVex2:p->adjVex1;
//pre!=-1&&p!=NULL
while(p!=NULL)
{
if(p->adjVex1==head && p->adjVex2!=pre)
p=p->nextarc1;
else if(p->adjVex2==head && p->adjVex1!=pre)
p=p->nextarc2;
else if(p->adjVex1==head && p->adjVex2==pre)
{
p=p->nextarc1;
break;
}
else if(p->adjVex2==head && p->adjVex1==pre)
{
p=p->nextarc2;
break;
}
}
if(p!=NULL)
{
return p->adjVex1==head?p->adjVex2:p->adjVex1;
}
else
return -1;
}
template<class ElemType, class WeightType> void MultiAdjListNetwork<ElemType, WeightType>::DFS3()
{
stack<int> s;
int p,cur,pre;
//MultiAdjListNetworkArc *p,*q;
for(int i=0; i<vexNum; i++) tag[i]=0;//初始化
for(int i=0; i<vexNum; i++)
{
cur=i;pre=-1;
while(tag[cur]==0||!s.empty())
{
while(tag[cur]==0)
{
cout<<vexTable[cur].data<<" ";
s.push(cur);
tag[cur]=1;
//初次访问,标记入栈
p=GetAdjVex(cur,pre);//p是cur的连通顶点
if(p==-1)
{
pre=cur;s.pop();
break;
}
else
{
pre=cur;
cur=p;
}
}
while(!s.empty())
{
cur=s.top();
p=GetAdjVex(cur,pre);
if(tag[p]==0)
{
pre=cur;
cur=p;
break;
}
else
{
pre=s.top();
s.pop();
}
}
}
}
}
template<class ElemType, class WeightType> void MultiAdjListNetwork<ElemType, WeightType>::BFS()
{
for(int i=0; i<vexNum; i++)
tag[i]=0;
queue<int> q;
int tmp,t;
MultiAdjListNetworkArc<WeightType> *p;
for(int i=0; i<vexNum; i++)
{
if(tag[i]==0)
{
tag[i]=1;
q.push(i);
cout<<setw(3)<<vexTable[i].data;
}
while(!q.empty())
{
tmp=q.front();
q.pop();
p=vexTable[tmp].firstarc;
while(p!=NULL)
{
t=(p->adjVex1==tmp?p->adjVex2:p->adjVex1);
if(tag[t]==0)
{
cout<<setw(3)<<vexTable[t].data;
tag[t]=1;
q.push(t);
}
p=NextArc(tmp,p);
}
}
}
}
template<class ElemType, class WeightType> void MultiAdjListNetwork<ElemType, WeightType>::Show()
{
MultiAdjListNetworkArc<WeightType> *p;
cout << "无向图有" << vexNum << "个点,分别为:";
for (int i = 0; i < vexNum; i++)
cout << vexTable[i].data << " ";
cout << endl;
cout << "无向图有" << arcNum << "条边"<<endl;
for (int i = 0; i < vexNum; i++)
{
cout<<"和" << vexTable[i].data << "有关的边:";
p = vexTable[i].firstarc;
while (p != NULL)
{
cout << vexTable[p->adjVex1].data << "<--"<<p->weight<<"-->" << vexTable[p->adjVex2].data << ",";
p=NextArc(i,p);
}
cout << endl;
}
}
邻接多重表与邻接表的对比
邻接表链接
在无向图的邻接多重表中,所需存储空间与表示无向图的邻接表相同。
在无向图的应用中,如果更加关注图的顶点,那么邻接表是不错的选择,但如果我们更关注边的操作,比如对已访问过的边做标记,删除某一条边等操作,那就意味着需要找到这条边的两个边表结点进行操作,若要删除某条边,需要对邻接表结构中相关的两个结点进行删除,显然这是比较繁琐的。
为了提高在无向图中操作顶点的效率,又有了邻接多重表的存储结构。邻接多重表与邻接表的区别在于,同一条边,在邻接多重表中要用两个结点表示,而在邻接表中只需要一个结点。此外,邻接多重表中增加了标志域用以标记该条边是否被搜索过,避免了同一条边的重复搜索。
至此,邻接多重表完毕#