高级数据结构-1
2. 堆
堆就是用数组实现的二叉树,所有它没有使用父指针或者子指针。堆根据“堆属性”来排序,“堆属性”决定了树中节点的位置。
堆的常用方法:
- 构建优先队列
- 支持堆排序
- 快速找出一个集合中的最小值(或者最大值)
堆分为两种:最大堆和最小堆,两者的差别在于节点的排序方式。
在最大堆中,父节点的值比每一个子节点的值都要大。在最小堆中,父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”,并且这个属性对堆中的每一个节点都成立。
这里有一篇介绍的非常好的文章:
https://www.jianshu.com/p/6b526aa481b1
堆排序
-
创建一个堆 H[0……n-1];
-
把堆首(最大值)和堆尾互换;
-
把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
-
重复步骤 2,直到堆的尺寸为 1。
#include top K问题
LeetCode374
https://leetcode-cn.com/problems/top-k-frequent-elements/solution/qian-k-ge-gao-pin-yuan-su-by-leetcode/
- 快速排序法
在快速排序中,每一轮排序都会将序列一分为二,左子区间的数都小于基准数,右子区间的数都大于基准数,而快速排序用来解决TopK问题,也是基于此的。N个数经过一轮快速排序后,如果基准数的位置被换到了i,那么区间[0,N-1]就被分为了[0,i-1]和[i+1,N-1],这也就是说,此时有N-1-i个数比基准数大,i个数比基准数小,假设N-1-i=X那么就会有以下几种情况:
①X=K。这种情况说明比基准数大的有K个,其他的都比基准数小,那么就说明这K个比基准数大的数就是TopK了;
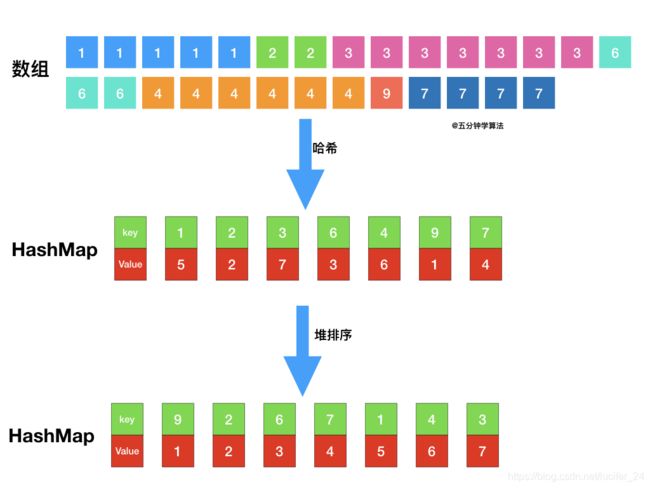
②X ③X>K。这种情况说明比基准数大的数超过了K个,那么就说明TopK必定位于[i+1,N-1]中,此时就应当继续在[i+1,N-1]找TopK,这样又成了TopK的一个子问题,也可以选择用递归解决。 代码思路如下(有点问题,超时) 出自LeetCode上面的题解: 题目最终需要返回的是前 kk 个频率最大的元素,可以想到借助堆这种数据结构,对于 kk 频率之后的元素不用再去处理,进一步优化时间复杂度。 首先依旧使用哈希表统计频率,统计完成后,创建一个数组,将频率作为数组下标,对于出现频率不同的数字集合,存入对应的数组下标即可。class Solution {
public:
int partition(vector<int> &nums, int l, int r){
int base = nums[l];
int base_index = l;
while(l<r){
while(l<r && nums[r]>base) --r;
while(l<r && nums[l]<base) ++l;
swap(nums[l], nums[r]);
}
nums[base_index] = nums[l];
nums[l] = base;
return l;
}
int find_topK_index(vector<int> &nums, int k, int l, int r){
int index = partition(nums, l, r);
int count = r-index;
if(count == k){
return index;
}
else if(count<k){
// cout<
https://leetcode-cn.com/problems/top-k-frequent-elements/solution/leetcode-di-347-hao-wen-ti-qian-k-ge-gao-pin-yuan-/
具体操作为:
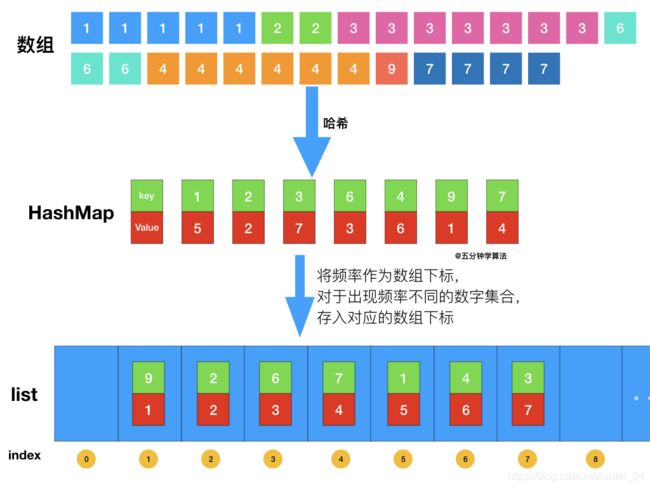
O(n)的复杂度,python写起来比较简单。
C++写也可以,需要用unsorted_map实现哈希表,用list容器实现桶。class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
times = {
}
for i in nums:
if i in times:
times[i] += 1
else:
times[i] = 1
bottom = [[] for _ in range(len(nums)+1)]
for i in times.keys():
time = times[i]
bottom[time].append(i)
res = []
for i in bottom[::-1]:
res.extend(i)
return res[0:k]