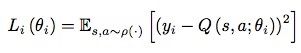【强化学习】Playing Atari with Deep Reinforcement Learning （2013）

Playing Atari with Deep Reinforcement Learning （2013）

这篇文章提出了第一个可以直接用强化学习成功学习控制policies的深度学习模型。
输入是raw pixels，输出是可以估计出为了的奖励的value function。

Introduction

学习直接从高维的感观输入（视觉，语音）去直接控制智能体是强化学习一个长期的挑战。一些成功的RL应用都是依赖于hand-crafted的特征。但是可以确定的是，特征的表示对于整个系统的表现力是很重要的

最近深度学习的进步是的提取高水平的特征成为了可能，然而强化学习仍然存在着一些挑战。

1. 很多成功的深度学习应用都需要大量的人工标注好的训练数据，然而RL只能从一个reward信号中学习，这个reward信号是非常稀少，有噪声并且有延迟的。
   Action和导致的reward之间可能会有成千上万的timestep延迟。
2. 深度学习算法假设数据样本是独立的，然而强化学习中的是一系列高度相关的状态。而且在RL中，随着算法学习，数据的分布也会改变，这对深度学习来说是一个大问题。

本文中的网络有一个变体的Q-learning算法来训练，用随机梯度下降更新权重。为了减轻数据相关联和分布不固定的问题，文章用了经验回放机制，随机采样先前的转变，因此可以平滑之前多个行为的训练分布（？）。

本文的目的是创造一个单独的神经网络智能体，它能够成功的学习去玩尽可能多的游戏，这个网络出了视频输入，reward，最终的信号，可能的action的集合不能从任何地方学习，就像人类玩家那样。此外，网络架构和用于训练的超参在游戏中都是保持不变的。（？）

Background
在每个timestep中，智能体从一系列action的集合中选择一个action a_t。这个action被传递到emulator中并且修正了它的内在的状态和游戏的分数。环境可能是随机的，emulator的内在状态不能被agent观察得到，它从emulator观察的是图像x_t. x_t是一个表示当前screen的像素值。此外，它收到代表了游戏分数变化的reward r_t。值得注意的是整体来说，游戏的分数取决于整个先前action和obervations的序列，关于一个action的feedback可能会在很多timestep后才会收到。

因为agent仅仅观察当前screen的图像，这个任务是被部分观察的并且每个emulator的状态是一直不同的。因此仅仅从当前screen x_t中完全理解当前状态是不可能的。因此我们认为action和obeservation的序列，s_t = x_1,a_1,—,a_t-1,x_t, 可以学习游戏策略。Emulator中的所有序列被设定在有限的timestep后停止。这种形式引起了一个规模大的但是有限的马尔可夫链，其中每个序列都是一个不同的状态。

智能体的目标是通过以一种可以最大化将来的reward的方式选择action再和emulator相互作用。作出一个假设，将来的reward被每个time-step的因子影响，定义在 t时刻，这个future discounted return为

T是游戏中止时的timestep，我们定义最佳的action-value function 为在看到很多序列s然后做了很多action a，后最大的期望返回值。

Pai是对于action的策略分布序列（或者是action的分布）。

最优的action-value function遵循贝尔曼方程。如果在下一个timestep，s’的最优值 was known for 所有可能的actions a‘最优策略就是选择可以最大化期望值的action a‘（？？）。

在强化学习算法后的一个基本的观点就是通过贝尔曼方程作为迭代更新去估计action-value function。

来说，这个方法是完全不现实的，因为action-value function对于每个sequence是被分来估计的，没有做任何的集合。 因此用一个函数近似的估计action-value function时很普遍的，

在强化学习中，这是一个典型的线性函数approximator，然而有时非线性的效果更好，例如神经网络。本文提出将一个有着weights theta的神经网络函数当作Q-network。那么这个Q-network就能通过最小化一个loss function的序列L_i(theta_i)来训练，

是一个在第i次迭代的target是squences s和 action a之间可能的分布，把这个分布当作behaviour distribution。在前一次迭代的参数theta_i-1 被固定，当优化loss function的时候。Target取决于网络的权重，这是和监督学习不同的地方。
求导后得到以下公式：
不同于计算上面梯度的全部expectations，采用随机梯度下降法优化loss function。如果权重在每个timestep后都被更新，expectation就会被来自与behaviour distribution的一个样本和emulator分布替代，那么就回到了之前熟悉的Q-learning算法了（？）

这个算法是无模型的，它之间用来自于emulator的样本解决了强化学习任务，而不是明确构建了emulator的估计（？）。它也是off-policy的（？），behaviour distribution总是通过贪婪策略选择的。

Related work

可能和本文最相似的算法就是neural fitted Q-learning（NFQ），NFQ通过RPROP算法优化loss function来更新Q-network中的参数。然而它用的是batch update，带来了一定的计算负担，而作者用的是随机梯度下降算法（但是随机梯度下降同时也会产生一些问题的啊？？）。Q-learning先前也包括经验回放和简单的神经网络，但是是从一个低维的state开始的而不是直接的视觉输入。

Deep Reinforcement Learning

Tesauro‘s TD-Gammon architecture 是一个在深度强化学习方面很好的开始，它的样本（s_t, a_t, r_t, s_t+1, a_t+1）是on-policy的，直接从算法和环境中的交互作用中得到。

和TD-Gammon不同，我们利用了一个叫做经验回放的技术，我们存储了agent在每个timestep的经历，在一个数据集D=e_1,…,e_N中e_t=(s_t,a_t,r_t,s_t+1)。在算法内部的loop中，采用了Q-learning更新或者（？）minibatch更新到经验的样本e中，这个样本是从经验池中随机选出来的（？）。在用了经验回放之后，agent根据贪婪算法选择了一个action。因为用任意长度的向量作为神经网络的输入是很困难的，所以Q-function通过一个函数固定了历史经历表示的长度。

和标准的在线Q-learning相比，这个方法有很多优点：

1. 在多次的权重更新过程中经验的每一步都有可能会被用到
2. 由于样本之间有很大的关联性，直接从连续的样本中学习有很大的问题，所有从样本中随机选择打破了这种关联性因此减小了参数更新的方差（？？）
3. on-policy中，当前的参数决定了下一个参数更新需要的数据样本，例如，如果要最大的action是向左走，那么训练样本将主要是来自左手边的样本。所有就会导致一个不想要的feedback loop，参数也会陷入局部极小，甚至发散。通过经验回放，behavior distribution会在先前多次状态下被平均，因此平滑了训练过程，比米娜了参数的发散或者抖动。值得注意的是，使用经验回放学习时，off-policy是必要的（因为根据off-policy的定义，用不是由当前的policy产生的数据，来更新当前的policy，就是foff-policy的方法）

实际操作中，经验回放仅仅保存了最近的N个样本点并且均匀的从数据集D中采样。在很多方面这个方法是有限的，因为经验池不能区分哪些转换是重要的，并且由于有限的memory sizeN，经常会被最近的数据覆盖。均匀采样也赋予了每个样本同样的重要性，更好的采样策略应该是侧重于那些可以学到更多的数据，比如prioritized sweeping（？）方法。

Preprocessing and model architecture
直接处理原始的atari画面（每一帧有着128color palette的210x160pixel图像），计算量会非常大，所以本文采用了一个基本的预处理步骤，目的是减小输入维度，将原石画面转位灰度图并且下采样到110x84的图像。最终的输入是由裁剪出一个84x84的image获得的。因为gpu的2d卷积神经网络需要方形的输入。Algorithm1中的function就是用这个预处理方法到last 4 frames of a history（？）并且将它们堆叠起来形成Q-function的输入。

由很多可能的方法用神经网络来参数化Q，因为Qmaps ，所以在之前的方法中，history和action已经用做神经网络的输入，主要的缺点是，计算每个action的Q值都需要一个分开的前向计算，这样会导致随着action的增加计算量也会增大。本文的办法是仅仅将状态作为输入。好处是在一个被给的状态下，可以对于每个可能的action都计算出相应的q值，并且只需要一次前向计算。

对于Atari games，神经网络的输入是84x84x4的图像，action数量是从4到18的。