OcTree可视化-matlab

来源：

https://www.mathworks.com/matlabcentral/mlc-downloads/downloads/submissions/40732/versions/3/download/zip/OcTree.zip

OcTree.m

classdef OcTree < handle
% OcTree point decomposition in 3D
%    OcTree is used to create a tree data structure of bins containing 3D
%    points. Each bin may be recursively decomposed into 8 child bins.
%
%    OT = OcTree(PTS) creates an OcTree from an N-by-3 matrix of point
%    coordinates.
%
%    OT = OcTree(...,'PropertyName',VALUE,...) takes any of the following
%    property values:
%
%     binCapacity - Maximum number of points a bin may contain. If more
%                   points exist, the bin will be recursively subdivided.
%                   Defaults to ceil(numPts/10).
%     maxDepth    - Maximum number of times a bin may be subdivided.
%                   Defaults to INF.
%     maxSize     - Maximum size of a bin edge. If any dimension of a bin 
%                   exceeds maxSize, it will be recursively subdivided.
%                   Defaults to INF.
%     minSize     - Minimum size of a bin edge. Subdivision will stop after 
%                   any dimension of a bin gets smaller than minSize.
%                   Defaults to 1000*eps.
%     style       - Either 'equal' (default) or 'weighted'. 'equal' 
%                   subdivision splits bins at their central coordinate
%                   (ie, one bin subdivides into 8 equally sized bins).
%                   'weighted' subdivision divides bins based on the mean
%                   of all points they contain. Weighted subdivision is
%                   slightly slower than equal subdivision for a large
%                   number of points, but it can produce a more efficient
%                   decomposition with fewer subdivisions.
%
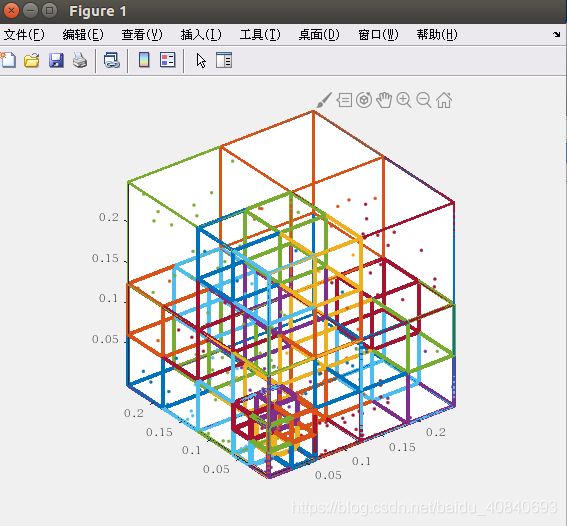
%    Example 1: Decompose 200 random points into bins of 20 points or less,
%             then display each bin with its points in a separate colour.
%        pts = (rand(200,3)-0.5).^2;
%        OT = OcTree(pts,'binCapacity',20);        
%        figure
%        boxH = OT.plot;
%        cols = lines(OT.BinCount);
%        doplot3 = @(p,varargin)plot3(p(:,1),p(:,2),p(:,3),varargin{:});
%        for i = 1:OT.BinCount
%            set(boxH(i),'Color',cols(i,:),'LineWidth', 1+OT.BinDepths(i))
%            doplot3(pts(OT.PointBins==i,:),'.','Color',cols(i,:))
%        end
%        axis image, view(3)
%
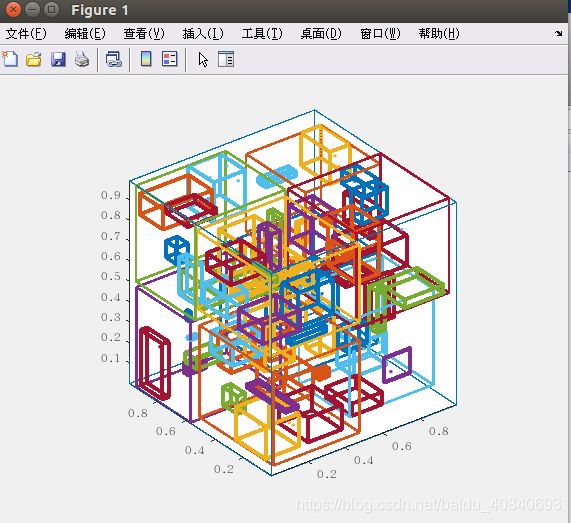
%    Example 2: Decompose 200 random points into bins of 10 points or less,
%             shrunk to minimallly encompass their points, then display.
%        pts = rand(200,3);
%        OT = OcTree(pts,'binCapacity',10,'style','weighted');
%        OT.shrink
%        figure
%        boxH = OT.plot;
%        cols = lines(OT.BinCount);
%        doplot3 = @(p,varargin)plot3(p(:,1),p(:,2),p(:,3),varargin{:});
%        for i = 1:OT.BinCount
%            set(boxH(i),'Color',cols(i,:),'LineWidth', 1+OT.BinDepths(i))
%            doplot3(pts(OT.PointBins==i,:),'.','Color',cols(i,:))
%        end
%        axis image, view(3)
%
%
% OcTree methods:
%     shrink            - Shrink each bin to tightly encompass its children
%     query             - Ask which bins a new set of points belong to.
%     plot, plot3       - Plots bin bounding boxes to the current axes.
%
% OcTree properties:
%     Points            - The coordinate of points in the decomposition.
%     PointBins         - Indices of the bin that each point belongs to.
%     BinCount          - Total number of bins created.
%     BinBoundaries     - BinCount-by-6 [MIN MAX] coordinates of bin edges.
%     BinDepths         - The # of subdivisions to reach each bin.
%     BinParents        - Indices of the bin that each bin belongs to.
%     Properties        - Name/Val pairs used for creation (see help above)
%
% See also qtdecomp.

%   Created by Sven Holcombe.
%   1.0     - 2013-03 Initial release
%   1.1     - 2013-03 Added shrinking bins and allocate/deallocate space
%
%   Please post comments to the FEX page for this entry if you have any
%   bugs or feature requests.
    
    properties
        Points;
        PointBins;
        BinCount;
        BinBoundaries;
        BinDepths;
        BinParents = zeros(0,1);
        Properties;
    end
    
    methods
        
        function this = OcTree(pts,varargin)
            % This is the OcTree header line
            validateattributes(pts,{'numeric'},...
                {'real','finite','nonnan','ncols', 3},...
                mfilename,'PTS')
            
            % Initialise a single bin surrounding all given points
            numPts = size(pts,1);
            this.BinBoundaries = [min(pts,[],1) max(pts,[],1)];
            this.Points = pts;
            this.PointBins = ones(numPts,1);
            this.BinDepths = 0;
            this.BinParents(1) = 0;
            this.BinCount = 1;
            
            % Allow custom setting of Properties
            IP = inputParser;
            IP.addParamValue('binCapacity',ceil(numPts)/10);
            IP.addParamValue('maxDepth',inf);
            IP.addParamValue('maxSize',inf);
            IP.addParamValue('minSize',1000 * eps);
            IP.addParamValue('style','equal');
            IP.parse(varargin{:});
            this.Properties = IP.Results;
            
            % Return on empty or trivial bins
            if numPts<2, return; end
            
            % Start dividing!
            this.preallocateSpace;
            this.divide(1);
            this.deallocateSpace;
        end
        
        % MATLAB performs better if arrays that grow are initialised,
        % rather than grown during a loop. These two functions do just that
        % before and after the identification of new beens.
        function preallocateSpace(this)
            numPts = size(this.Points,1);
            numBins = numPts;
            if isfinite(this.Properties.binCapacity)
                numBins = ceil(2*numPts/this.Properties.binCapacity);
            end
            this.BinDepths(numBins) = 0;
            this.BinParents(numBins) = 0;
            this.BinBoundaries(numBins,1) = 0;
        end
        function deallocateSpace(this)
            this.BinDepths(this.BinCount+1:end) = [];
            this.BinParents(this.BinCount+1:end) = [];
            this.BinBoundaries(this.BinCount+1:end,:) = [];
        end
        
        function divide(this, startingBins)
            % Loop over each bin we will consider for division
            for i = 1:length(startingBins)
                binNo = startingBins(i);
                
                % Prevent dividing beyond the maximum depth
                if this.BinDepths(binNo)+1 >= this.Properties.maxDepth
                    continue;
                end
                
                % Prevent dividing beyond a minimum size                
                thisBounds = this.BinBoundaries(binNo,:);
                binEdgeSize = diff(thisBounds([1:3;4:6]));
                minEdgeSize = min(binEdgeSize);
                maxEdgeSize = max(binEdgeSize);
                if minEdgeSize < this.Properties.minSize
                    continue;
                end
                
                % There are two conditions under which we should divide
                % this bin. 1: It's bigger than maxSize. 2: It contains
                % more points than binCapacity.
                oldCount = this.BinCount;
                if nnz(this.PointBins==binNo) > this.Properties.binCapacity
                    this.divideBin(binNo);
                    this.divide(oldCount+1:this.BinCount);
                    continue;
                end
                if maxEdgeSize>this.Properties.maxSize
                    this.divideBin(binNo);
                    this.divide(oldCount+1:this.BinCount);
                    continue;
                end
            end
        end
        
        function divideBin(this,binNo)
            % Gather the new points (a bit more efficient to copy once)
            binPtMask = this.PointBins==binNo;
            thisBinsPoints = this.Points(binPtMask,:);
            
            % Get the old corner points and the new division point
            oldMin = this.BinBoundaries(binNo,1:3);
            oldMax = this.BinBoundaries(binNo,4:6);
            if strcmp('weighted',this.Properties.style) && any(binPtMask)
                newDiv = mean(thisBinsPoints,1);
            else
                newDiv = mean([oldMin; oldMax], 1);
            end
            
            % Build the new boundaries of our 8 subdivisions
            minMidMax = [oldMin newDiv oldMax];
            newBounds = minMidMax([...
                1 2 3 4 5 6;
                1 2 6 4 5 9;
                1 5 3 4 8 6;
                1 5 6 4 8 9;
                4 2 3 7 5 6;
                4 2 6 7 5 9;
                4 5 3 7 8 6;
                4 5 6 7 8 9]);
            
            % Determine to which of these 8 bins each current point belongs
            binMap = cat(3,[0 0 0],[0 0 1],[0 1 0],[0 1 1],...
                [1 0 0],[1 0 1],[1 1 0],[1 1 1]);
            gtMask = bsxfun(@gt, thisBinsPoints, newDiv);
            [~,binAssignment] = max(all(bsxfun(@eq,gtMask,binMap),2),[],3);
            % [~, binAssignment] = ismember(gtMask,binMap,'rows'); % A little slower than above.
            
            % Make the new bins and reassign old points to them
            newBinInds = this.BinCount+1:this.BinCount+8;
            this.BinBoundaries(newBinInds,:) = newBounds;
            this.BinDepths(newBinInds) = this.BinDepths(binNo)+1;
            this.BinParents(newBinInds) = binNo;
            this.PointBins(binPtMask) = newBinInds(binAssignment);
            this.BinCount = this.BinCount + 8;
        end
        
        function shrink(this)
            % Shrink all bins to bound only the points they contain
            % WARNING: this operation creates gaps in the final space not
            % covered by a bin. Only shrink OcTree structures when you only
            % intend to use the points used to create the tree to query the
            % tree space.
            binChildren = arrayfun(@(i)find(this.BinParents==i),1:this.BinCount,'Un',0)';
            binIsLeaf = cellfun(@isempty, binChildren);
            for i = find(binIsLeaf(:))'
                binShrink_recurse(i, true)
            end
            
            function binShrink_recurse(binNo, isLeafBin)
                % Build a list of all points that fall within one of the
                % bins to be checked, and the list of which point falls in
                % which bin.
                oldBoundaryMin = this.BinBoundaries(binNo,1:3);
                oldBoundaryMax = this.BinBoundaries(binNo,4:6);
                if isLeafBin
                    % Shrink bin based on child POINTS
                    ptsMask = this.PointBins==binNo;
                    if ~any(ptsMask)
                        % No points, shrink the bin to infinitely small
                        proposedBoundaries = [oldBoundaryMin oldBoundaryMin];
                    else
                        pts = this.Points(ptsMask,:);
                        proposedBoundaries = [...
                            max([oldBoundaryMin; min(pts,[],1)]) ...
                            min([oldBoundaryMax; max(pts,[],1)])];
                    end
                else
                    % Shrink bin based on child BINS
                    childBoundaries = this.BinBoundaries(binChildren{binNo},:);
                    proposedBoundaries = [min(childBoundaries(:,1:3),[],1) max(childBoundaries(:,4:6),[],1)];
                end
                
                if ~isequal(proposedBoundaries, [oldBoundaryMin oldBoundaryMax])
                    % We just shrunk the boundary. Make it official and
                    % check the parent
                    this.BinBoundaries(binNo,:) = proposedBoundaries;
                    parentBin = this.BinParents(binNo);
                    if parentBin>0
                        binShrink_recurse(parentBin, false)
                    end
                end
            end
        end
        
        function binNos = query(this, newPts, queryDepth)
            % Get the OcTree bins that new query points belong to.
            %
            % BINS = OT.query(NEWPTS) searches the OcTree object OT and
            % returns an N-by-1 vector of BINS giving the bin index in
            % which each of the N points in NEWPTS is contained. For any
            % query points outside all bins in OT, the index -1 is
            % returned.
            %
            % BINS = OT.query(NEWPTS,DEPTH) restricts the search to DEPTH
            % levels in the OT bin tree. Note that the first bin
            % (containing all other bins in OT) has DEPTH = 1.

            if nargin<3
                queryDepth = max(this.BinDepths);
            end
            
            numPts = size(newPts,1);
            newPts = permute(newPts,[3 2 1]);
            binNos = ones(numPts,1)*-1;
                        
            binChildren = arrayfun(@(i)find(this.BinParents==i),1:this.BinCount,'Un',0)';
            binIsLeaf = cellfun(@isempty, binChildren);
            ptQuery_recurse(1:numPts, this.BinParents==0, 0)
            
            function ptQuery_recurse(newIndsToCheck_, binsToCheck, depth)
                % Build a list of all points that fall within one of the
                % bins to be checked, and the list of which point falls in
                % which bin.
                boundsToCheck = this.BinBoundaries(binsToCheck,:);
                [ptInBounds, subBinNo] = max(all(...
                    bsxfun(@ge, newPts(:,:,newIndsToCheck_), boundsToCheck(:,1:3)) & ...
                    bsxfun(@le, newPts(:,:,newIndsToCheck_), boundsToCheck(:,4:6))...
                    ,2),[],1);
            
                if ~all(ptInBounds)
                    % Special case usually when depth=0, where a point may
                    % fall outside the bins entirely. This should only
                    % happen once so let's fix it once and let subsequent
                    % code rely on all points being in bounds
                    binNos(newIndsToCheck_(~ptInBounds)) = -1;
                    newIndsToCheck_(~ptInBounds) = [];
                    subBinNo(~ptInBounds) = [];
                end
                binNosToAssign = binsToCheck(subBinNo);
                newIndsToAssign = newIndsToCheck_;
                binNos(newIndsToAssign) = binNosToAssign;
                
                % Allow a free exit when we reach a certain depth
                if depth>=queryDepth
                    return;
                end
                
                % Otherwise, for all of the points we just placed into
                % bins, check which of the children of those bins those
                % same points fall into
                [unqBinNos, ~, unqGrpNos] = unique(binNosToAssign);
                for i = 1:length(unqBinNos)
                    thisPtMask = unqGrpNos==i;
                    if ~binIsLeaf(unqBinNos(i))
                        ptQuery_recurse(newIndsToCheck_(thisPtMask), binChildren{unqBinNos(i)}, depth+1)
                    end
                end
                
            end
        end
        
        function h = plot(this,varargin)
            % OcTree.plot plots bin bounding boxes of an OcTree object
            %
            % H = OT.plot('name',value,...) allows you to specify any
            % properties of the bounding box lines that you would normally
            % supply to a plot(...,'name',value) command, and returns plot
            % object handles (one per bin) to H.
            hold on;
            h = zeros(this.BinCount,1);
            for i = 1:this.BinCount
                binMinMax = this.BinBoundaries(i,:);
                pts = cat(1, binMinMax([...
                    1 2 3; 4 2 3; 4 5 3; 1 5 3; 1 2 3;...
                    1 2 6; 4 2 6; 4 5 6; 1 5 6; 1 2 6; 1 2 3]),...
                    nan(1,3), binMinMax([4 2 3; 4 2 6]),...
                    nan(1,3), binMinMax([4 5 3; 4 5 6]),...
                    nan(1,3), binMinMax([1 5 3; 1 5 6]));
                h(i) = plot3(pts(:,1),pts(:,2),pts(:,3),varargin{:});
            end
        end
        function h = plot3(this,varargin)
            % OcTree.plot plots bin bounding boxes of an OcTree
            %
            % See also OcTree.plot
            h = this.plot(varargin{:});
        end
    end
end

main.m

pts = (rand(200,3)-0.5).^2;
OT = OcTree(pts,'binCapacity',20);        
figure
boxH = OT.plot;
cols = lines(OT.BinCount);
doplot3 = @(p,varargin)plot3(p(:,1),p(:,2),p(:,3),varargin{:});
for i = 1:OT.BinCount
   set(boxH(i),'Color',cols(i,:),'LineWidth', 1+OT.BinDepths(i))
   doplot3(pts(OT.PointBins==i,:),'.','Color',cols(i,:))
end
axis image, view(3)



pts = rand(200,3);
OT = OcTree(pts,'binCapacity',10,'style','weighted');
OT.shrink
figure
boxH = OT.plot;
cols = lines(OT.BinCount);
doplot3 = @(p,varargin)plot3(p(:,1),p(:,2),p(:,3),varargin{:});
for i = 1:OT.BinCount
   set(boxH(i),'Color',cols(i,:),'LineWidth', 1+OT.BinDepths(i))
   doplot3(pts(OT.PointBins==i,:),'.','Color',cols(i,:))
end
axis image, view(3)