利用棋盘格图案完成相机标定

摄像机标定

单孔摄像机（照相机）会给图像带来很多畸变。畸变主要有两种：径向畸变和切想畸变。如下图所示，用红色直线将棋盘的两个边标注出来，但是你会发现棋盘的边界并不和红线重合。所有我们认为应该是直线的也都凸出来了。

所以需要进行相机标定

棋盘格标定

OpenCV使用棋盘格板进行标定，如下图所示。为了标定相机，我们需要输入一系列三维点和它们对应的二维图像点。在黑白相间的棋盘格上，二维图像点很容易通过角点检测找到。而对于真实世界中的三维点呢？由于我们采集中，是将相机放在一个地方，而将棋盘格定标板进行移动变换不同的位置，然后对其进行拍摄。所以我们需要知道(X,Y,Z)的值。但是简单来说，我们定义棋盘格所在平面为XY平面，即Z=0。对于定标板来说，我们可以知道棋盘格的方块尺寸，例如30mm，这样我们就可以把棋盘格上的角点坐标定义为(0,0,0)，(30,0,0)，(60,0,0)，···，这个结果的单位是mm。
  3D点称为object points，2D图像点称为image points。

检测棋盘格角点

为了找到棋盘格模板，我们使用openCV中的函数cv2.findChessboardCorners()。我们也需要告诉程序我们使用的模板是什么规格的，例如88的棋盘格或者55棋盘格等，建议使用x方向和y方向个数不相等的棋盘格模板。下面实验中，我们使用的是86的棋盘格，每个方格边长是20mm，即含有75的内部角点。这个函数如果检测到模板，会返回对应的角点，并返回true。当然不一定所有的图像都能找到需要的模板，所以我们可以使用多幅图像进行定标。除了使用棋盘格，我们还可以使用圆点阵，对应的函数为cv2.findCirclesGrid()。
  
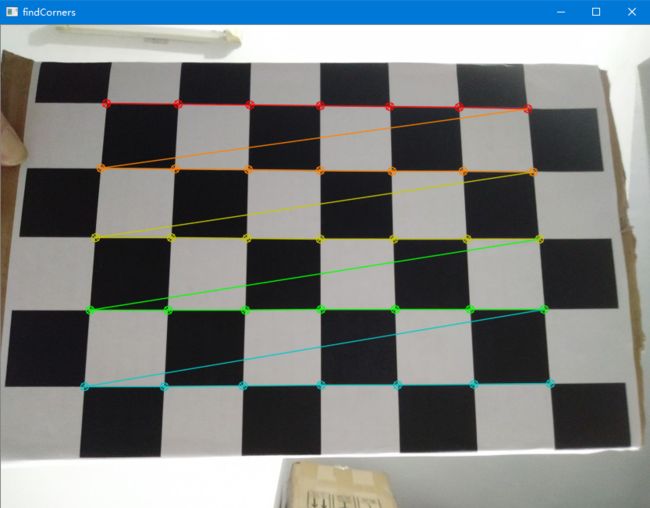
找到角点后，我们可以使用cv2.cornerSubPix()可以得到更为准确的角点像素坐标。我们也可以使用cv2.drawChessboardCorners()将角点绘制到图像上显示。如下图所示：

用手机拍摄了14张棋盘格图片，并将分辨率调整到832x624，既将原分辨率缩小20%

标定

通过上面的步骤，我们得到了用于标定的三维点和与其对应的图像上的二维点对。我们使用cv2.calibrateCamera()进行标定，这个函数会返回标定结果、相机的内参数矩阵、畸变系数、旋转矩阵和平移向量。

ret: 0.49780289785568144
内参数矩阵:
 [[662.65760958   0.         411.7554067 ]
 [  0.         643.62036576 312.36138692]
 [  0.           0.           1.        ]]
畸变系数:
 [[ 1.75605608e-01 -7.32319628e-01  1.74170917e-04  1.07586378e-04
   8.15249028e-01]]
旋转向量: [array([[ 0.06848192],
       [-0.11021601],
       [ 0.19342032]]), array([[ 0.08989725],
       [-0.2535112 ],
       [-0.02463974]]), array([[0.09910906],
       [0.25820579],
       [0.00510581]]), array([[-0.14623837],
       [ 0.00945762],
       [ 0.001026  ]]), array([[ 0.20322661],
       [-0.02586824],
       [-0.00751255]]), array([[ 0.20643026],
       [-0.087326  ],
       [-0.03735129]]), array([[ 0.05928905],
       [-0.31920575],
       [-0.01057067]]), array([[0.07565014],
       [0.21659039],
       [0.00056359]]), array([[0.20951298],
       [0.23124036],
       [0.05598759]]), array([[0.02498131],
       [0.05687095],
       [0.00956028]]), array([[-0.1802921 ],
       [-0.03419934],
       [-0.00123688]])]
平移向量: [array([[-2.36878258],
       [-2.90199425],
       [ 7.32577822]]), array([[-2.62155616],
       [-1.99853277],
       [ 6.49172398]]), array([[-3.28628108],
       [-2.26570619],
       [ 7.62271742]]), array([[-3.06893891],
       [-2.59407061],
       [ 7.86211726]]), array([[-3.09682038],
       [-2.22304886],
       [ 7.07652815]]), array([[-2.73779139],
       [-1.77450487],
       [ 6.88388611]]), array([[-2.28058289],
       [-2.10824111],
       [ 6.15841957]]), array([[-3.35984547],
       [-2.08592   ],
       [ 7.32862568]]), array([[-3.70854886],
       [-2.24924643],
       [ 7.31569625]]), array([[-3.26049871],
       [-2.235856  ],
       [ 7.17300778]]), array([[-3.03386901],
       [-2.40116135],
       [ 7.3427078 ]])]

由于手机拍摄的图片分辨率过高，原图：4160X3120的分辨率，相当于把图片分辨率缩小20%。
根据摄像头自身参数

焦距f：4mm

像素大小Δx=Δy​：1.12um

计算可知：fx=fΔx=3571.42857、fy=fΔy=3571.42857

u0=4160/2=2080、v0=3120/2=1560

通过相机标定的值：

fx=662.65760958 、fy=643.62036576

u0=411.7554067、v0=312.36138692

换算以后：

fx=3313.28805 、 fy=3218.10183

u0=2058.77703 、 v0=1561.80693

由于预先图片分辨率缩减了20%，再加上摄像头的误差，加上我自己拍摄的因素，虽然误差达到了200多，但是最后得到的这个结果，我觉得也是合理的。

去畸变

第三步我们已经得到了相机内参和畸变系数，在将图像去畸变之前，我们还可以使用cv.getOptimalNewCameraMatrix()优化内参数和畸变系数，通过设定自由自由比例因子alpha。当alpha设为0的时候，将会返回一个剪裁过的将去畸变后不想要的像素去掉的内参数和畸变系数；当alpha设为1的时候，将会返回一个包含额外黑色像素点的内参数和畸变系数，并返回一个ROI用于将其剪裁掉。

然后我们就可以使用新得到的内参数矩阵和畸变系数对图像进行去畸变了。

反投影误差

通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差，这个值就是反投影误差。

total error: 0.07951334176924868

完整代码如下：

#coding:utf-8
import cv2
import numpy as np
import glob

# 找棋盘格角点
# 阈值
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
#棋盘格模板规格
w = 9
h = 6

# 世界坐标系中的棋盘格点,例如(0,0,0), (1,0,0), (2,0,0) ....,(8,5,0)，去掉Z坐标，记为二维矩阵
objp = np.zeros((w*h,3), np.float32)
objp[:,:2] = np.mgrid[0:w,0:h].T.reshape(-1,2)

# 储存棋盘格角点的世界坐标和图像坐标对
objpoints = [] # 在世界坐标系中的三维点
imgpoints = [] # 在图像平面的二维点

images = glob.glob('test_pic/*.jpg')
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)  #图像二值化

    # 找到棋盘格角点
    ret, corners = cv2.findChessboardCorners(gray, (w,h),None)

    # 如果找到足够点对，将其存储起来
    if ret == True:
        cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        objpoints.append(objp)
        imgpoints.append(corners)

        # 将角点在图像上显示
        cv2.drawChessboardCorners(img, (w,h), corners, ret)
        cv2.imshow('findCorners',img)
        cv2.waitKey(500)
#cv2.destroyAllWindows()#删除建立的全部窗口

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
#相机标定 返回标定结果、相机的内参数矩阵、畸变系数、旋转矩阵和平移向量


# 保存相机参数
np.savez('C.npz', mtx=mtx, dist=dist, rvecs=rvecs, tvecs=tvecs)
print("ret:", ret)
print("内参数矩阵:\n", mtx)
print("畸变系数:\n", dist)
print("旋转向量:", rvecs)  # 外参数
print("平移向量:", tvecs)  # 外参数



# 去畸变
img2 = cv2.imread('test_pic/left05.jpg')
h,  w = img2.shape[:2]
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),0,(w,h)) # 自由比例参数
dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)

# 根据前面ROI区域裁剪图片
#x,y,w,h = roi
#dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.jpg',dst)

# 反投影误差
total_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    total_error += error
print("total error: {}".format(total_error/len(objpoints)))

2. 在1基础上，使用同一相机，将棋盘格放在前方1m左右固定，然后使用线性方法进行相对位姿估计，然后评价结果的合理性。

在上问的摄像机标定中，我们已经得到了摄像机矩阵，畸变系数等。有了这些信息我们就可以估计图像中图案的姿势，比如目标对象是如何摆放，如何旋转等。对一个平面对象来说，我们可以假设 Z=0，这样问题就转化成摄像机在空间中是如何摆放（然后拍摄）的。所以，如果我们知道对象在空间中的姿势，我们就可以在图像中绘制一些 2D 的线条来产生 3D 的效果。

完整代码：

import cv2
import numpy as np
import glob

# 加载相机标定的数据
with np.load('C.npz') as X:
    mtx, dist, _, _ = [X[i] for i in ('mtx', 'dist', 'rvecs', 'tvecs')]


def draw(img, corners, imgpts):
    """
    在图片上画出三维坐标轴
    :param img: 图片原数据
    :param corners: 图像平面点坐标点
    :param imgpts: 三维点投影到二维图像平面上的坐标
    :return:
    """
    corner = tuple(corners[0].ravel())
    cv2.line(img, corner, tuple(imgpts[0].ravel()), (255, 0, 0), 5)
    cv2.line(img, corner, tuple(imgpts[1].ravel()), (0, 255, 0), 5)
    cv2.line(img, corner, tuple(imgpts[2].ravel()), (0, 0, 255), 5)
    return img


# 初始化目标坐标系的3D点
objp = np.zeros((6 * 7, 3), np.float32)
objp[:, :2] = np.mgrid[0:7, 0:6].T.reshape(-1, 2)
# 初始化三维坐标系
axis = np.float32([[3, 0, 0], [0, 3, 0], [0, 0, -3]]).reshape(-1, 3)  # 坐标轴
# 加载打包所有图片数据
images = glob.glob('test_pic/*.jpg')
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # 找到图像平面点坐标点
    ret, corners = cv2.findChessboardCorners(gray, (7, 6), None)
    if ret:
        # PnP计算得出旋转向量和平移向量
        _, rvecs, tvecs, _ = cv2.solvePnPRansac(objp, corners, mtx, dist)
        print("旋转变量", rvecs)
        print("平移变量", tvecs)
        # 计算三维点投影到二维图像平面上的坐标
        imgpts, jac = cv2.projectPoints(axis, rvecs, tvecs, mtx, dist)
        # 把坐标显示图片上
        img = draw(img, corners, imgpts)
        cv2.imshow('img', img)
        cv2.waitKey(500)

#cv2.destroyAllWindows()