从Java角度看区块链实践系列4:基于原理手写实现SHA-256算法以及Merkle树算法
上一节课,我们讲到Merkle树的原理,其本质是一种哈希二叉树结构,叶子借贷你的value源于数据的哈希,非叶子节点的value则是根据它左右两个孩子节点进行双哈希计算得出。
Merkle树算法在区块链中被广泛使用,其应用面包括零知识证明、文件完整性校验等领域。
现在,让我们进入主题,实战手写SHA-256算法以及Merkle树。
加密算法
目前,加密算法主要分为对称加密算法、非对称加密算法以及不可逆加密算法三大类。
对称加密算法
对称加密算法是应用较早的加密算法,对称加密算法加密的解密的密钥相同,其密钥实现主要有分组密码和序列密码两种实现方式。对称加密算法的主要特点是算法公开、计算量小、加密速度快、效率高,但加解密使用同一密钥,安全性得不到保障。目前,主流对称加密算法有DES、3DES、IDEA以及美国国家标准局的AES。
非对称加密算法
由于加密和解密使用不同密钥,故称为“非对称加密”,其密钥分为公钥和私钥,公私钥成对配合使用。非对称加密算法可以实现数字签名。常见的有RSA算法、美国国家标准局与技术研究院(NIST)提出的DSA算法。特点是加密速度慢、效率低。(在签名部分会详细讲解RSA原理)
不可逆加密算法
不可逆加密算法加密不需要使用密钥,输入明文后由系统直接经过加密算法处理成密文,是一种单向摘要加密算法,加密后的算法难以被破解,校验则需要使用原有数据使用同种加密算法加密,对结果进行比较。目前,被广泛使用的主要是RSA公司研发的MD5以及美标局推荐的基于SHS(Secure Hash Standard,安全哈希标准)标准的算法等。
哈希散列函数
维基这样定义它:
散列函数是一种可以从任意大小的数据创建固定大小数据的函数。散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。该函数将数据打乱混合,重新创建一个叫做散列值(hash values,hash codes,hash sums,或hashes)的指纹。
主要特点是压缩性强、计算简单、加密结果单向性,通过哈希碰撞概率问题保证安全性。它将无限的内容压缩到有限位数的取值范围内,不可避免有效概率出现哈希碰撞的可能性,因此哈希函数必须具备良好的抗碰撞性。
目前,哈希算法主要分MD系列(MD4、MD5、HAVAL)和SHA系列(SHA-1、SHA-256),这里介绍SHA系列的SHA256。
1byte字节=8bit位,一个十六进制的字符的长度为4bit位。
SHA-1算法
SHA-1算法的输入长度限制在264位,输入消息按照512位一个组进行分组处理,输出结果是160位的消息摘要。SHA-1算法的速度高、实现简单。
SHA-2算法
SHA-2算法输出长度可取224位、256位、384位、512位,分别对应SHA-224、SHA-256、SAH-384、SHA-512,另外还有SHA-512/224、SHA-512/256,这两个算法比之前的算法具备更高的安全性和输出长度的灵活性。这些变体除了生成摘要的长度、循环运行的次数等一些细微差异之外,基本结构是一致的。
SHA-3算法
美标局选择Keccak算法作为SHA-3的加密标准,Keccak算法具有良好的加密性能以及抗解密能力。
SHA-256的数学基础
自然数:大于零的整数。
质数:指在大于1的自然数中,除了1和它本身意外不再有其他因数的自然数。
取模运算:又称“模除”,即求两个自然数做除法运算的余数。若有自然数 a、b,则 a % b = c 或 a mod b = c,当 a < b 时,c = a。关于模的运算比较多,除了简单的四则运算以外还有我们后续签名算法会用到的模逆元。
高位/低位:所谓高位/即是二进制数字,做位移运算时,左边被移除的bit位,低位则相反,为位移运算后不足的bit位。
二进制左移(<<):m< 例如5左移4位(由于Java int类型占32bit位,所以这里按32位二进制演示): 5的二进制:0000 0000 0000 0000 0000 0000 0000 0101 向左移4位:0000 0000 0000 0000 0000 0000 0101 0000(不足补0,结果为十进制80) 二进制右移(>>):m>>n把整数m表示的二进制数右移n位,m为正数,高位全部补0;m为负数,高位全部补1。m>>n即相当于m除以2的n次方,得到的为整数时,即为结果。如果结果为小数,此时会出现两种情况: 若m为正数,得到的商会无条件 的舍弃小数位; 若m为负数,舍弃小数部分,然后把整数部分加+1得到位移后的值。 无符号右移( >>> ):m>>>n:整数m表示的二进制右移n位,不论正负数,高位都补0。 位与( & ):逐个比较两个二进制字符串,若两个都为1才为1,其他情况均为0。例如 5 & 3: 5的二进制:0000 0000 0000 0000 0000 0000 0000 0101 3的二进制:0000 0000 0000 0000 0000 0000 0000 0011 位与结果: 0000 0000 0000 0000 0000 0000 0000 0001 位或( | ):逐个比较两个二进制字符串,若两个都为0才为0,其他情况均为1。 位非( ~ ):对单个二进制字符串,二进制位的内容取反。是1则变为0,0则变为1。 位异或( ^ ):逐个比较两个二进制字符串,若位值相同,则为0,反之则为1。例如: 5的二进制:0000 0000 0000 0000 0000 0000 0000 0101 3的二进制:0000 0000 0000 0000 0000 0000 0000 0011 位异或后: 0000 0000 0000 0000 0000 0000 0000 0110 bit代表二进制位,byte代表字节,word是SHA256算法中的最小运算单元,称为“字”(Word)。 1 byte = 8 bit 1 int = 1 word = 4 byte = 4*8 = 32 bit 涉及到的逻辑函数Java实现表: SHA-256被广泛应用于比特币区块链,基本所有涉及摘要加密的地方比特币都选用了SHA-256,同时在公链项目中也随处可见SHA-256的应用。 由于雪崩效应,即使消息有很小的改变,也将导致最终Hash结果的不同。 对于任意长度的消息,SHA-256都会输出一个256bit位的Hash摘要,这个摘要通常是一个长度为64的十六进制字符串,相当于是4个个长度为32-byte字节的数组。SHA-256算法中最小运算单元称为“字”(Word),一个字是32位。 加密过程: 1、设置初始化常量; 2、对输入消息进行补位,补位后的长度为512bit位的倍数; 3、按照每个块512bit位对补位后的消息进行分块: 4、对每个块执行一系列复杂的逻辑运算,最终得到哈希摘要: 常量初始化 1、初始化8个原始哈希H0,取自然数前8个素数/质数(2,3,5,7,11,13,17,19)的平方根的小数部分的前32bit位。 比如: 于是,质数2的平方根的小数部分取前32bit用16进制表示就为 2、初始化64个常数密钥,取自自然数中前面64个素数的 立方根的小数部分的前32bit位,用16进制表示, 则相应的常数序列如下: 我们使用 消息预处理——补位 补位操作遵循如下方程式: 为什么是448? 因为在补位的第一步的预处理后,第二步会附加上一个64bit的数据,用来表示原始报文的长度信息。而448+64=512,正好拼成了一个完整的结构。 我们以SHA256(“abc”)为例: 因此,其二进制形式为:01100001 01100010 01100011,长度 1、补1,即直接在二进制消息尾部添加 1; 例如:消息“abc”的二进制位,补1后 01100001 01100010 01100011 1。 2、补0,个数为 例如:代入 3、补入消息长度 例如:消息“abc”的二进制长度为24,则最后进行的补位操作就是将24的二进制形式 00011000。 调用pad()方法可以获取到补位的结果,代码实现<单击一键,代码尽显>: 加密计算Hash摘要 1、将补位后的消息分解成n个块,每一个块512bit。 用java实现时,我们不需要按块“存储”,因此可以省略此步。 2、遍历所有区块,将单个区块从16 word重构成64 word。 对于每一块,将块分解为16个32-bit的big-endian的字,记为w[0], …, w[15]。当前区块的第t个“字”我们用 2.1 前16个字直接由消息的第t个块分解得到。经过第一步进行区块分组后,每个区块都包含了16 word。 2.2 其余的字由如下迭代公式得到: 3、循环对每个“块”加密,也就是说需要循环64次。 经过步骤二后,W将成为具备64 word,加密的过程如下图: 代码实现<单击一键,代码尽显>: 经过64轮后,代码中的H就是最终SHA-256加密的结果。 Merkle树原理在上一节,我们已经详细阐述过,这里就直接贴实现的代码了<复习快速跳转>。 定义叶子节点<单击一键,代码尽显> Merkle树计算<单击一键,代码尽显> 这一节,我们剖析了在区块链的底层核心所涉及的加密算法,深入了解如今被广泛使用的SHA-256算法的实现原理,其通过简单的位移取模操作生成摘要,SHA256的抗碰撞性保证了信息的安全。 之后我们实战了Merkle树算法,从实战中可以了解更多它的优缺点,也可以检验上篇我们讲解的Merkle原理,进而让我们在了解区块链的道路上更近一步。 好啦,今天我们到这里就结束啦! 近期由于搬家找房子后续文章可能会有所延后发布,文章有不足之处,欢迎指出,我将不断完善之~ 最后,给大家奉上后续Java实战计划安排表: 讲解相关安全事故以及预防措施。 讲解有关合约审计的相关知识,让你能熟练一名合约审计员所需要的掌握的知识点。传授给你最高单日审核10+合约的程序员的所有知识。 参考文献: 维基 — 散列函数 维基 — SHA-2算法 SHA-256原理 Java工具库 — HuTool 《区块链底层设计Java实战》SHA-256涉及到的运算符与进制换算表
公式逻辑运算符
Java逻辑运算符
含 义
∧
&
按位“与”
¬
~
按位“补/非”
⊕
|
按位“异/或”
![]()
Integer.rotateRight()
循环右移n个bit
![]()
>>>
无符号右移n个bit
逻辑函数
Java实现
![]()
private static int smallSig0(int x) {
return Integer.rotateRight(x, 7) ^ Integer.rotateRight(x, 18)
^ (x >>> 3);
}
![]()
private static int smallSig1(int x) {
return Integer.rotateRight(x, 17) ^ Integer.rotateRight(x, 19)
^ (x >>> 10);
}
![]()
private static int ch(int x, int y, int z) {
return (x & y) | ((~x) & z);
}
![]()
private static int maj(int x, int y, int z) {
return (x & y) | (x & z) | (y & z);
}
![]()
private static int bigSig0(int x) {
return Integer.rotateRight(x, 2) ^ Integer.rotateRight(x, 13)
^ Integer.rotateRight(x, 22);
}
![]()
private static int bigSig1(int x) {
return Integer.rotateRight(x, 6) ^ Integer.rotateRight(x, 11)
^ Integer.rotateRight(x, 25);
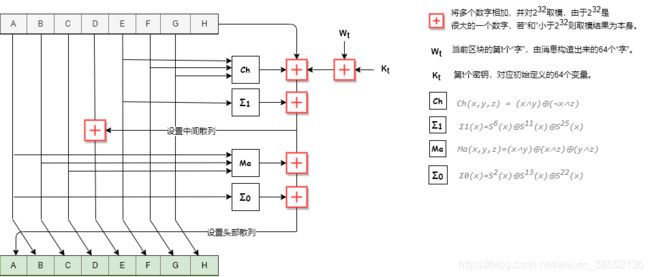
}SHA-256
![]()
SHA-256原理详解
![]()
0x6a09e667。 private static final int[] H0 = {0x6a09e667, 0xbb67ae85, 0x3c6ef372,
0xa54ff53a, 0x510e527f, 0x9b05688c, 0x1f83d9ab, 0x5be0cd19};![]() 表示第t个密钥。
表示第t个密钥。 private static final int[] K = {0x428a2f98, 0x71374491, 0xb5c0fbcf,
0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74,
0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786,
0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc,
0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85,
0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb,
0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70,
0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3,
0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f,
0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7,
0xc67178f2};![]()
原始字符
ASCII码
二进制格式
a
97
01100001
b
98
01100010
c
99
01100011
![]() 。
。![]() ,代入消息长度
,代入消息长度 ![]() 可求得;
可求得;![]() 算得
算得 ![]() ,因此补 423个0。由于448 < 512,因此,可忽略掉后面的mod 512(对整数取模时,若整数小于模数,则取模结果为本身)。因此补位后,01100001 01100010 01100011 10000000……00000000。
,因此补 423个0。由于448 < 512,因此,可忽略掉后面的mod 512(对整数取模时,若整数小于模数,则取模结果为本身)。因此补位后,01100001 01100010 01100011 10000000……00000000。![]() 的64位二进制内容,若长度的二进制不足64位,则在长度前面添加0,知道二进制字符串长度为64。
的64位二进制内容,若长度的二进制不足64位,则在长度前面添加0,知道二进制字符串长度为64。 /**
* 填充给定消息的长度
* 512位(64字节)的倍数,包括添加 1位,k 0位以及消息长度为64位整数。
*
* @param message 要填充的消息,String.getBytes()可获得消息的字节数组。
* @return 一个带有填充消息字节的新数组。
*/
public static byte[] pad(byte[] message) {
final int blockBits = 512;
final int blockBytes = blockBits / 8;
// 新消息长度:原始长度 + (补位的)1位 + 填充8字节长度(也就是64bit)
int newMessageLength = message.length + 1 + 8;
int padBytes = blockBytes - (newMessageLength % blockBytes);
newMessageLength += padBytes;
// 将消息复制到扩展数组
final byte[] paddedMessage = new byte[newMessageLength];
System.arraycopy(message, 0, paddedMessage, 0, message.length);
// 第一步,补位:在消息末尾补上一位"1"。0b代表二进制,10000000 是二进制的128
paddedMessage[message.length] = (byte) 0b10000000;
// 第二步,跳过,因为我们已经设置了padBytes数组的长度,所以内部所有元素已经是0了(默认值)
// 第三步,补入消息长度l的64位二进制的8字节整数,(java使用的是byte,1 byte = 8 bit)
int lenPos = message.length + 1 + padBytes;
ByteBuffer.wrap(paddedMessage, lenPos, 8).putLong(message.length * 8);
return paddedMessage;
}![]() 表示。
表示。 /**
* 块数组
*/
private static final int[] W = new int[64];
public static byte[] hash(byte[] message) {
// ……省略部分代码
System.arraycopy(words, i * 16, W, 0, 16);
// ……省略部分代码
}![]()
/**
* 块数组
*/
private static final int[] W = new int[64];
public static byte[] hash(byte[] message) {
// ……省略部分代码 smallSig1为 σ1 函数,smallSig0为 σ0 函数
for (int t = 16; t < W.length; ++t) {
// 根据加法交换律,修改先后顺序不印象最终结果
W[t] = smallSig1(W[t - 2])
+ W[t - 7]
+ smallSig0(W[t - 15])
+ W[t - 16];
}
// ……省略部分代码
}
/**
* 块数组
*/
private static final int[] W = new int[64];
public static byte[] hash(byte[] message) {
// ……省略部分代码
/*
3、循环对“块”加密:也就是说循环64次。
例如:对“abc”加密时,就相当于依次对 c、b、a进行加密,c的加密结果,保存到a位置
*/
// 设 TEMP = H,H是初始变量,即8个初始hash值,也就是前8个质数的平方根的前32bit位。
System.arraycopy(H, 0, TEMP, 0, H.length);
// 在TEMP上操作
for (int t = 0; t < W.length; ++t) {
// t1 = H[7] + Ch(H[4],H[5],H[6]) + Σ1(H[4])
int t1 = TEMP[7]
+ ch(TEMP[4], TEMP[5], TEMP[6]) + K[t] + W[t]
+ bigSig1(TEMP[4]);
// t2 = Ma(H[0],H[1],H[2]) + Σ0(H[0])
int t2 = maj(TEMP[0], TEMP[1], TEMP[2]) + bigSig0(TEMP[0]);
System.arraycopy(TEMP, 0, TEMP, 1, TEMP.length - 1);
// 设置中间散列
TEMP[4] += t1;
// 设置头部散列 t1 + t2
TEMP[0] = t1 + t2;
}
// 将TEMP中的值添加到H中的值
for (int t = 0; t < H.length; ++t) {
H[t] += TEMP[t];
}
// ……省略部分代码
}Java实现Merkle树
@Data
public class TreeNode {
/**
* 左子节点
*/
private TreeNode left;
/**
* 右子节点
*/
private TreeNode right;
/**
* (孩子)节点数据
*/
private String data;
/**
* SHA-256的data
*/
private String hash;
public TreeNode(){}
public TreeNode(String data) {
this.data = data;
this.hash = DigestUtil.sha256Hex(data);
}
}
package org.lmx.common.merkle;
import cn.hutool.core.collection.CollectionUtil;
import cn.hutool.core.util.ObjectUtil;
import cn.hutool.crypto.digest.DigestUtil;
import lombok.extern.slf4j.Slf4j;
import java.util.ArrayList;
import java.util.List;
/**
* 功能描述:Merkle算法实现
*
* @program: block-chain-j
* @author: LM.X
* @create: 2020-03-31 14:53
**/
@Slf4j
public class MerkleTree {
/**
* 交易列表
*/
private List总结
目录
内容
P2P网络实战
这一篇将为大家带来Java实现P2P通讯网络的实战。
区块链共识系列
学习共识系列你将会了解到目前最为完整的共识算法发展史,还能学习到Java实战实现共识算法。包括:RAFT共识、经典的PWD、PWD、DPOS共识、最新的PoET、POB共识、以及混合共识。
签名算法系列:RSA签名算法
这一篇你将学习到RSA的密码学、RSA签名原理及实战
签名算法系列:ECC椭圆曲线签名
学习ECC椭圆曲线加密算法你讲收获椭圆曲线密码学、椭圆曲线数学等相关知识。
区块链安全
Solidity合约编写
讲解合约实现原理、实战合约。包含ERC20、ERC-223、ERC-721、NEP系列、TRC系列等合约编写等实战。
合约审计
匿名性研究
讲解区块链匿名性相关实现方案及实战。
实战大流量交易所钱包设计
讲解交易所钱包相关设计,涵盖安全、用户意图分析、交易加速等。
交易所难点突破
包含交易所业务与架构选型、分布式撮合引擎实战等内容。
区块浏览器
讲解如何搭建区块浏览器、动辄百GB的区块数据,如何快速检索等内容。
区块链钱包
包含有关钱包的设计等内容。
其他
包含区块链发展历史,主流币趋势分析等内容。