python_day0D 算法和数据结构:顺序表
目录
00x00:从一道面试题开始
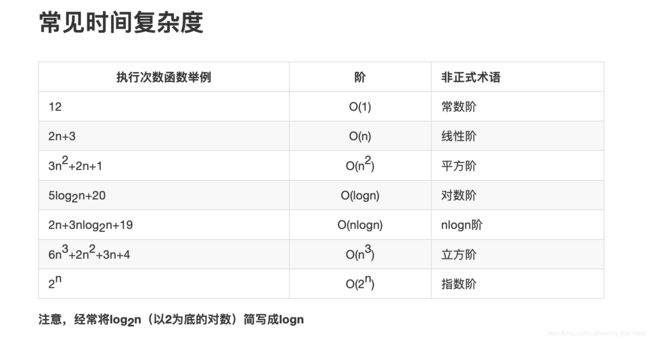
0x01 时间复杂度拾遗:
0x02 测算器 与 构造列表各个方法时间复杂度比较
0x03 顺序表
0x04 顺序表的操作
Python中的顺序表
list的基本实现技术
00x00:从一道面试题开始
思路:枚举法
用两层或者三层for循环枚举a,b,c所有的取值,然后在循环内判断是否满足等式,如果满足就输出。
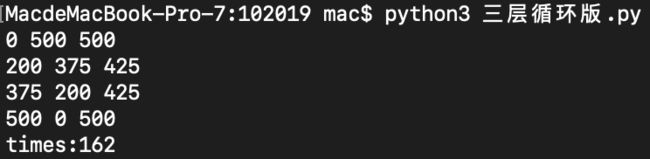
三层循环版:
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
for c in range(0,1001):
if a+b+c == 1000 and a**2 + b**2 == c**2:
print(a,b,c)
end_time = time.time()
print("times:%d"%(end_time-start_time))时间:
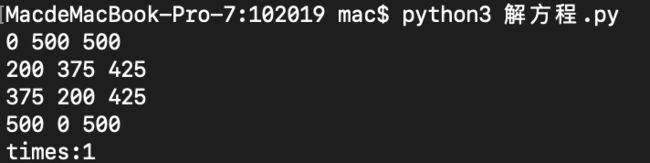
两层循环版:
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
if a**2 + b**2 == (1000-a-b)**2:
print(a,b,(1000-a-b))
end_time = time.time()
print("times:%d"%(end_time-start_time))时间:
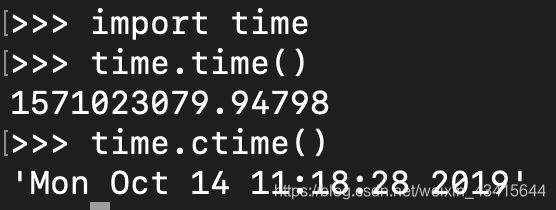
[注意]:
time.time()返回的是当前时间的浮点数类型,即是一个时间戳
time.ctime()返回的当前时间的字符串类型
0x01 时间复杂度拾遗:
0x02 测算器 与 构造列表各个方法时间复杂度比较
#coding:utf-8
from timeit import Timer
#测试构造列表的四种方式
def test1():
li = []
for i in range(10000):
li.append(i)
def test2():
li = []
for i in range(10000):
li += [i]
def test3():
li = [i for i in range(10000)]
def test4():
li = list(range(10000))
def test5():
li = []
for i in range(10000):
li.extend([i])
def test6():
li = []
for i in range(10000):
li.insert(0,i)
#插入i使其成为第0个元素
#即头插法
def test7():
li = []
for i in range(10000):
li = li + [i]
#构造测算器
timer1 = Timer("test1()","from __main__ import test1")
#第一个参数为要测试的函数名
#第二个参数是运行代码时进行的必要设置
#即从当前文件将test1函数导入到Timer中
#Timer是一个类,返回一个测算器对象
#启动测算器对象,测1000次,求运行时间平均值(s)
t1 = timer1.timeit(1000)
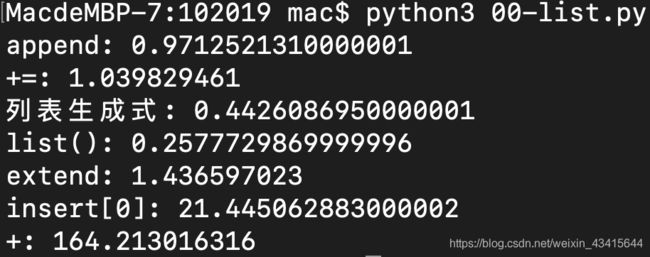
print("append:",t1)
timer2 = Timer("test2()","from __main__ import test2")
t2 = timer2.timeit(1000)
print("+=:",t2)
timer3 = Timer("test3()","from __main__ import test3")
t3 = timer3.timeit(1000)
print("列表生成式:",t3)
timer4 = Timer("test4()","from __main__ import test4")
t4 = timer4.timeit(1000)
print("list():",t4)
timer5 = Timer("test5()","from __main__ import test5")
t5 = timer5.timeit(1000)
print("extend:",t5)
timer6 = Timer("test6()","from __main__ import test6")
t6 = timer6.timeit(1000)
print("insert[0]:",t6)
timer7 = Timer("test7()","from __main__ import test7")
t7 = timer7.timeit(1000)
print("+:",t7)
执行结果:
建议:少用+号!
补充:
表示用[1,2,3,4,5,6]来替换list列表的前三位,即先将前三位删除,然后将[1,2,3,4,5,6]给插入进去
0x03 顺序表
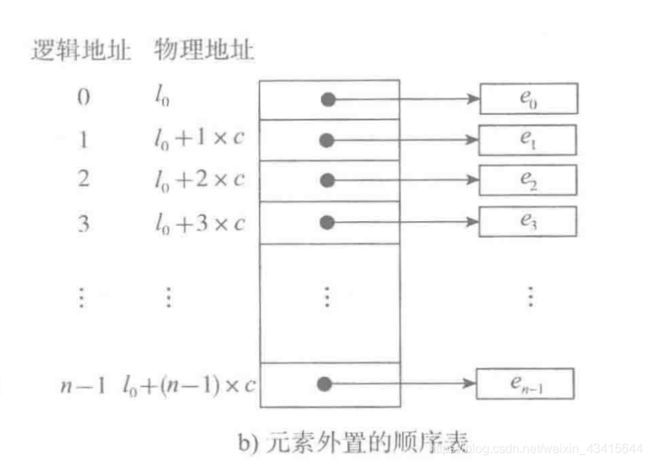
python中的列表可以存储不同类型的数据,如果这些数据在内存中连续存储,那么列表查询操作时指针偏移量是不一样的。
那么python是如何解决的呢?python采用了哈希表的结构,连续存储列表中数据的地址,32位机地址是4个字节。这样每次查询,指针的偏移量就相同,先取到数据的地址,然后根据地址取到数据即可。
顺序表的结构:
数据区一定是申请的一段连续的存储空间,那么表头信息和数据区两者的存储空间该如何安排呢?
两种方式优劣:
一体式结构存在扩容问题,对于插入操作,如果需要扩容的话,就需要申请新的一段内存,对于一体式结构,就需要将表头和数据区和新数据全部拷贝到新内存。而对于分离式结构,就只需要将数据区拷贝就可以了。
0x04 顺序表的操作
Python中的顺序表
Python中的list和tuple两种类型采用了顺序表的实现技术,具有前面讨论的顺序表的所有性质。
tuple是不可变类型,即不变的顺序表,因此不支持改变其内部状态的任何操作,而其他方面,则与list的性质类似。
list的基本实现技术
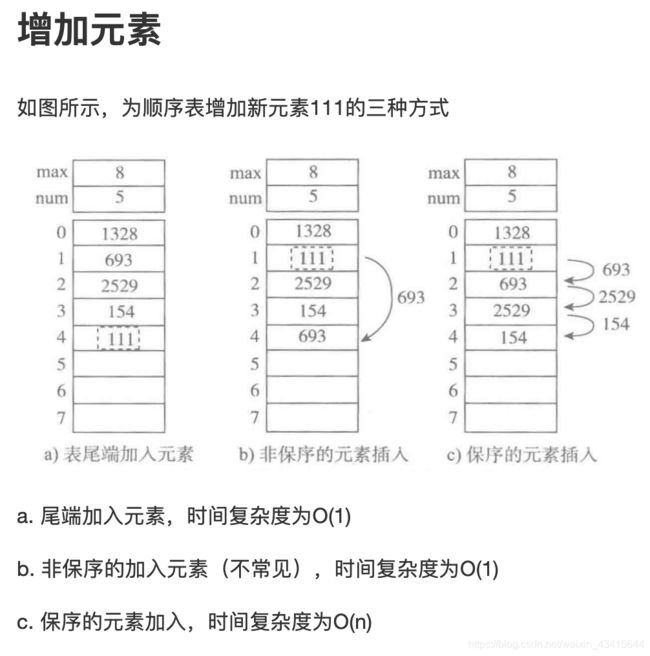
Python标准类型list就是一种元素个数可变的线性表,可以加入和删除元素,并在各种操作中维持已有元素的顺序(即保序),而且还具有以下行为特征:
-
基于下标(位置)的高效元素访问和更新,时间复杂度应该是O(1);
为满足该特征,应该采用顺序表技术,表中元素保存在一块连续的存储区中。
-
允许任意加入元素,而且在不断加入元素的过程中,表对象的标识(函数id得到的值)不变。
为满足该特征,就必须能更换元素存储区,并且为保证更换存储区时list对象的标识id不变,只能采用分离式实现技术。
在Python的官方实现中,list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x) (或 list.insert(len(list), x),即尾部插入)比在指定位置插入元素效率高的原因。
在Python的官方实现中,list实现采用了如下的策略:在建立空表(或者很小的表)时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大(目前的阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式,是为了避免出现过多空闲的存储位置。