一次综合的、深入浅出的压感的回顾与总结
压感是什么？
压感即压缩采样（Compressive Sampling），也叫压缩感知( Compressive Sensing )，后面具体解释或猜测为什么这么个叫法？
直接上图：
压感的作用就是将一个长的信号（
）变成（压缩采样）成一个短的多的信号（
），而且满足一定的条件（后面具体讨论），能够由短的信号（
）精确地恢复长的信号（），而重构需要做得仅仅是解一个优化问题。
————————————————————————————————————————————————————
压感针对的对象？
压感针对的时离散的信号，而且这个离散的信号是可以进行稀疏表示的。（这个离散的信号的来源包括本身是离散的还有模拟信号经过采样得到的离散信号）
————————————————————————————————————————————————————
压感最关键的三个问题？
一、信号的稀疏表示问题：
信号能否进行稀疏表示，是压感应用的前提条件。
如 x = [1 0 0 0 1 0]，其中只有2个1，可认为时稀疏的。
若 N维实信号 x 的稀疏表示为： 
，其中 
叫正交基字典矩阵，
叫系数向量，且 
是K稀疏的。
何为K稀疏？
即 x 稀疏表示后的结果 
只有K个元素不为0，其他全为0。
二、观测矩阵的设计问题：
如何设计一个平稳的、与稀疏变换基不相关的 
维的观测矩阵 
(M<
用公式表示为：
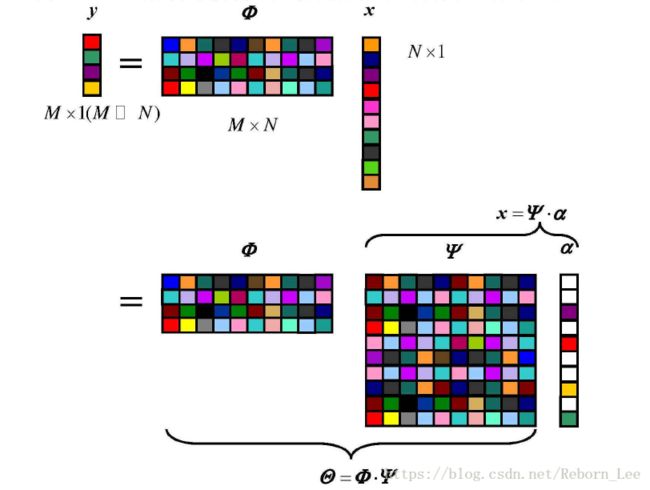
用示意图表示为：
观测矩阵 
的每一行可以看作一个传感器，它与系数（x）相乘，获取了信号（x）的部分信息。
上述过程相当于对信号 x 执行一个压缩观测，就可以得到 M 个线性观测 
，这些少量的观测中则包含了重构信号 x 的足够信息。
三、信号的重建问题：
从观测向量 y 中恢复 x 是一个解线性方程组的问题，但由于 
是一个未知数个数大于方程个数（
）的病态方程（M是方程个数，N是未知数个数），它有无穷多解。
但由 
可知：
， 虽然从 y 中恢复 
也是一个病态问题，但因为 
是K稀疏的，这样未知数个数大大减少，使得信号重构成为可能。
到底要满足什么样的条件时，信号才能够重构呢？
只要矩阵 
中任意 2K 列都是线性独立的 ,那么至少存在一个 K-稀疏的系数向量 
满足 
。换言之 ,在满足上述要求的情况下 ,通过求解一个如下的优化问题，
就能从观测 y 、观测矩阵 
和字典矩阵 
中近乎完美的重建信号 x。
到此，压感的三个重要问题算是告一段落。
————————————————————————————————————————————————————
压感的一些难点问题：
（1）压缩采样是在离散信号的背景下提出来的理论；
（2）对多维矩阵进行矩阵相乘运算，在硬件实现上具有一定的难度；
（3）需要一套从连续信号直接得到离散观测点的方案；
其次还有如下一些小问题：
理论上，任何离散信号都能进行稀疏表示，关键问题时找到一个能稀疏表示的变换域 
。目前，对稀疏变换域的研究大多集中在正交变换基字典上，但也有关于过完备字典的研究；（可以展开讨论）
观测矩阵 
的设计能够影响到信号能够精确重构，因此观测矩阵设计关乎成败。研究发现高斯随机矩阵，具有良好的性质，满足观测矩阵的要求，当然还有其他的，有待继续研究；
压感的应用问题，都是需要努力的方向。
————————————————————————————————————————————————————
压感的遗憾：
目前压感所针对的信号时离散信号，而自然界几乎所有的信号都是模拟信号，如何利用压感去处理模拟信号？如果在奈奎斯特框架下去采样模拟信号，在进入压感的框架下处理，压感优势何在？这不免让人感到失望。
不过，压感也有着其自身的价值，对离散信号处理也不错嘛。这个数字世界需要处理的数字信号还是很多的。
————————————————————————————————————————————————————
暴风雨后的彩虹：模拟信息转换器（AIC）
模拟信息转换器无需将模拟信号数字化，可直接采样模拟信号，得到离散的观测样点。典型的AIC系统框图如下：
（科普性内容，具体查看相关资料）
模拟信息转换的硬件实现时一个可以研究的方向。
应用：Rice大学的单反相机。